Темы
Информатика(2656 задач)
--->
173 задач
<---
#1027
Темы:
[Сортировка подсчетом]
[Жадный алгоритм]
Задана таблица, содержащая буквы, а также набор слов, которые необходимо вычеркнуть. Каждая следующая буква слова содержится в таблице рядом с предыдущей. Требуется вычеркнуть все слова из таблицы и вывести оставшиеся буквы.
Петя разгадывает головоломку, которая устроена следующим образом. Дана квадратная таблица размера NxN, в каждой клетке которой записана какая-нибудь латинская буква. Кроме того, дан список ключевых слов. Пете нужно, взяв очередное ключевое слово, найти его в таблице. То есть найти в таблице все буквы этого слова, причем они должны быть расположены так, чтобы клетка, в которой расположена каждая последующая буква слова, была соседней с клеткой, в которой записана предыдущая буква (клетки называются соседними, если они имеют общую сторону — то есть соседствуют по вертикали или по горизонтали). Например, на рисунке ниже показано, как может быть расположено в таблице слово olympiad.
| P | O | L | T | E |
| R | W | Y | M | S |
| O | A | I | P | T |
| B | D | A | N | R |
| L | E | M | E | S |
Когда Петя находит слово, он вычеркивает его из таблицы. Использовать уже вычеркнутые буквы в других ключевых словах нельзя.
После того, как найдены и вычеркнуты все ключевые слова, в таблице остаются еще несколько букв, из которых Петя должен составить слово, зашифрованное в головоломке.
Помогите Пете в решении этой головоломки, написав программу, которая по данной таблице и списку ключевых слов выпишет, из каких букв Петя должен сложить слово, то есть какие буквы останутся в таблице после вычеркивания ключевых слов.
Входные данные
В первой строке входного файла записаны два числа N (1N10) и M (0M200). Следующие N строк по N заглавных латинских букв описывают ребус. Следующие M строк содержат слова. Слова состоят только из заглавных латинских букв, каждое слово не длиннее 200 символов. Гарантируется, что в таблице можно найти и вычеркнуть по описанным выше правилам все ключевые слова.
Выходные данные
В единственную строку выходного файла выведите в любом порядке буквы, которые останутся в таблице.
Примеры
Входные данные
5 3 POLTE RWYMS OAIPT BDANR LEMES OLYMPIAD PROBLEM TEST
Выходные данные
AENRSW
#1028
| 0 | 2 | 2 | 2 | 2 |
| 0 | 2 | 2 | 2 | 2 |
| 1 | 1 | 2 | 2 | 2 |
| 1 | 1 | 0 | 0 | 0 |
На поле NxM клеток (N строк и M столбцов) положили K прямоугольников один поверх другого в случайном порядке. Длины сторон прямоугольников выражаются целым числом клеток. Прямоугольники не выходят за границы поля. Границы прямоугольников совпадают с границами клеток поля.
Получившуюся ситуацию записали в таблицу чисел (каждой клетке поля соответствует клетка таблицы). Если клетка поля не закрыта прямоугольником, то в соответствующую клетку таблицы записали число 0. Если же клетка закрыта одним или несколькими прямоугольниками, то в соответствующую клетку таблицы записали число, соответствующее номеру самого верхнего прямоугольника, закрывающего эту клетку.
По содержимому таблицы требуется определить положение и размеры прямоугольников.
Гарантируется, что во входных данных содержится информация, которой достаточно для однозначного определения размеров прямоугольников.
Входные данные
В первой строке входного файла записаны целые числа N, M, K (1N200, 1M200, 1K255). Далее следует N строк по M чисел в каждой — содержимое таблицы. Все числа в таблице целые, находятся в диапазоне от 0 до K включительно.
Выходные данные
В выходной файл необходимо выдать K строк. Каждая строка должна описывать соответствующий ее номеру прямоугольник четырьмя числами R C H W (R и C должны описывать координаты левого нижнего угла прямоугольника, а H и W — координаты правого верхнего угла). Числа должны разделяться пробелом.
Примеры
Входные данные
4 5 2 0 2 2 2 2 0 2 2 2 2 1 1 2 2 2 1 1 0 0 0
Выходные данные
0 0 2 2 1 1 5 4
#1029
Темы:
[Простые игры]
[Сортировка подсчетом]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Выпуклый N-угольник разбит непересекающимися диагоналями на треугольники. (Многоугольник называется выпуклым, если любая его диагональ лежит внутри него.) Требуется покрасить каждую сторону и каждую проведенную диагональ в красный или синий цвет так, чтобы у каждого треугольника были стороны как красного, так и синего цвета.
Требуется привести любую из допустимых раскрасок.
Входные данные
В первой строке записано одно число N (4N100) - количество вершин многоугольника.
Далее следуют N–3 строки, в каждой из которых записана пара натуральных чисел — номера вершин, которые соединяет диагональ. Считается, что все вершины занумерованы последовательно натуральными числами от 1 до N.
Выходные данные
В выходном файле должны быть 2N–3 строки. Каждая строка содержит 3 числа: номера вершин, которые соединяет данная сторона или диагональ и цвет (1 - синий, 2 - красный), в который Вы красите данную сторону или диагональ.
Примечание
Возможный ответ на перый тест:
3 4 1
2 3 2
1 2 1
1 3 2
1 4 1
Возможный ответ на второй тест:
5 6 1
4 5 2
3 4 1
3 5 2
2 3 1
1 2 2
1 3 1
1 5 2
1 6 1
Примеры
Входные данные
4 1 3
Выходные данные
Входные данные
6 1 3 3 5 5 1
Выходные данные
#1030
Темы:
[Обход в ширину]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Представьте, что вы состоите на службе во внешней разведке Межгалактического Альянса Республиканских Сил (МАРС). Одному из агентов разведки крупно не повезло, и он был захвачен на засекреченной космической базе. К счастью, внешней разведке МАРС удалось заполучить план этой базы. И вот теперь вам поручено разработать план побега.
База представляет собой прямоугольник размером NхM, со всех сторон окружённый стенами, и состоящий из квадратных отсеков единичной площади. База снабжена K выходами, до одного из которых агенту необходимо добраться. В некоторых отсеках базы находятся стены. Ваш агент может перемещаться из отсека в любой из четырех соседних с ним, если в том отсеке, куда он хочет переместиться, нет стены.
Кроме того, база снабжена системой гипертуннелей, способных перемещать агента из одного отсека базы (вход в гипертуннель) в другой (выход из гипертуннеля). Когда агент находится в отсеке, где есть вход в гипертуннель, он может (но не обязан) им воспользоваться.
Начальное положение вашего агента известно. Вам необходимо найти кратчайший путь побега (то есть путь, проходящий через минимальное количество отсеков).
Входные данные
В первой строке входного файла записаны числа N и M (2≤N≤100, 2≤M≤100), задающие размеры базы: N — количество строк в плане базы, M — количество столбцов. Во второй строке записаны начальные координаты агента XA,YA (1≤XA≤N, 1≤YA≤M). Первая координата задает номер строки, вторая — номер столбца. Строки нумеруются сверху вниз, столбцы слева направо.
Далее следуют N строк по M чисел, задающих описание стен внутри базы: 1 соответствует стенке, 0 — её отсутствию.
Далее в отдельной строке записано число H (0≤H≤1000) — количество гипертуннелей. В последующих H строках идут описания гипертуннелей. Каждый гипертуннель задается 4 числами: X1, Y1, X2, Y2 (1≤X1,X2≤N; 1≤Y1,Y2≤M) — координатами входа и выхода гипертуннеля. Никакие два гипертуннеля не имеют общего входа.
После этого в отдельной строке следует число K (1≤K≤10) — количество выходов с базы. В последующих K строках идут описания выходов с базы. Каждый выход задается двумя координатами X и Y (1≤X≤N; 1≤Y≤M).
Гарантируется, что начальные координаты агента не совпадают ни с одним из выходов и он не стоит в отсеке, занятом стеной. Никакие входы и выходы гипертуннелей, а также выходы с базы не находятся в отсеках, занятых стенами. Никакой вход в гипертуннель не совпадает с выходом с базы
Выходные данные
Если побег невозможен, выведите единственную строку с надписью "Impossible". В противном случае в первой строке выдайте число L - количество отсеков в кратчайшем пути побега. В последующих L строках последовательно выведите координаты отсеков кратчайшего пути побега. Если решений несколько, то выведите любое из них.
Примеры
Входные данные
4 5 2 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 2 1 2 1 4 3 1 1 4 1 2 4
Выходные данные
4 2 1 3 1 1 4 2 4
#1032
ограничение по времени на тест
3.0 second;
ограничение по памяти на тест
64 megabytes
В комнате решили сделать паркетный пол. Причем есть задумка выложить на полу некоторый узор.
Плитки паркета, которыми выкладывается пол комнаты, состоят из квадратиков 1x1, каждый из которых может быть либо белым, либо черным. В свою очередь, комната имеет размеры NxM. На плане комнаты указано, какой квадрат комнаты какого цвета должен быть.
Существует несколько форм паркетных плиток:
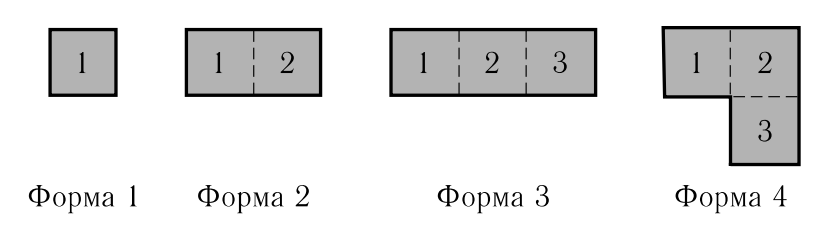
Квадратики одной паркетной плитки могут быть окрашены по-разному. Может существовать несколько типов плиток одинаковой формы, но окрашенных по-разному. Плитки разных типов могут иметь разную стоимость. Количество плиток каждого типа не ограничено. Плитки разрешается как угодно поворачивать (на углы, кратные 90 градусам). Не разрешается разламывать плитки, а также класть их лицевой стороной вниз.
Изначально, какая-то часть пола может уже быть выложена плиткой.
Требуется определить минимальную стоимость плитки, необходимой для того, чтобы замостить оставшуюся часть комнаты.
Входные данные
В первой строке входного файла записаны три числа: N, M (размеры комнаты) и K (количество доступных видов плитки). 1≤N≤8, 1≤M≤8, 1≤K≤10. Далее идет описание желаемой раскраски пола. Описание представляет собой N строчек по M чисел в каждой, где 0 обозначает белый цвет, 1 — черный, 2 — то, что квадрат уже выложен плиткой. В последних K строчках находятся описания доступных типов плитки в следующем формате:
<форма> <стоимость> <окраска>
<Форма> — это число от 1 до 4, описывающее форму плитки (см. рисунок выше)
<Стоимость> — это натуральное число, не превосходящее 10000, задающее стоимость одной плитки такого типа
<Окраска> — это от одного до трех чисел 0 или 1. Количество чисел совпадает с количеством квадратиков, из которых состоит плитка. Числа задают цвета квадратиков плитки в том порядке, в каком квадратики пронумерованы на рисунке.
Выходные данные
В выходной файл выведите единственное число — минимальную стоимость укладки или –1, если требуемым образом уложить плитку невозможно.
Примеры
Входные данные
4 3 3 2 2 2 2 0 0 2 1 2 2 2 2 2 10 0 0 1 5 1 4 6 0 0 1
Выходные данные
15
Выбрано
:
|