#1038

Гексагон

Темы: [Условный оператор (if)]

Источники: [ Личные олимпиады, Открытая олимпиада школьников, 2005, Задача D ]

Поле для игры в новую игру "Гексагон" разбито 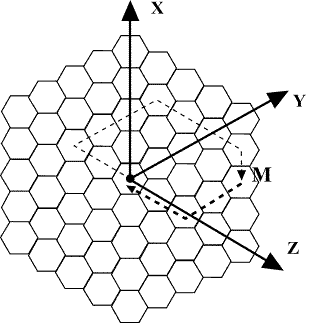на шестиугольники (см. рисунок). Игрок, стартуя из некоторого начального шестиугольника, сделал несколько ходов. Каждый ход заключается в премещении фишки в соседний шестиугольник (имеющий с тем, где находилась фишка до начала хода, общую сторону) — тем самым, ход делается вдоль одного из направлений X, Y или Z (см. рисунок). Игрок записал все свои ходы, причем если фишка двигалась вдоль какого-либо направления несколько раз подряд, то в записи это обозначается указанием направления и количества ходов, которые были сделаны.

Напишите программу, которая найдет кратчайший (по количеству совершаемых ходов)путь в начальную клетку из той, где фишка оказалась после ходов игрока.

Входные данные

В первой строке входного файла записано число N — количество строк в записи перемещений фишки (1N100). Далее идет N строк с записью ходов: в каждой строке записана сначала большая буква X, Y или Z, задающая направление, затем пробел, и число, задающее количество ходов в данном направлении (число может быть и отрицательным, если игрок перемещал фишку параллельно оси, но в направлении, противоположном направлению оси). Все числа по модулю не превышают 200.

Выходные данные

В выходной файл выведите описание кратчайшего пути обратно в начальную клетку в том же формате, в каком описание задано во входном файле (за исключением ограничений). Все числа, определяющие количество ходов в каком-либо направлении, должны быть ненулевыми.

Примеры

Входные данные

4
Z -2
Y 3
Z 3
X -1

Выходные данные

#1039

Магия Копперфильда

Темы: [Простые игры] [Конструктив]

Источники: [ Личные олимпиады, Открытая олимпиада школьников, 2005, Задача E ]

Дана прямоугольная таблица. Фишка в таблице может перемещаться в любое место на K ходов. Требуется последовательно убрать все ячейки таблицы, кроме одной, задавая количество ходов, на которые должна сходить фишка, и координаты удаляемых клеток. Фишка должна оказаться в единственной оставшейся клетке.

Всемирно известный маг Дэвид Копперфильд любит показывать следующий трюк. Квадрат из N столбцов и N строк, в каждой клетке которого находится какая-нибудь картинка, появляется на экране телевизора. Пусть все картинки пронумерованы следующим образом:

1	2	…	N
N+1	N+2	…	*2N**
:	:	…	:
N*(N–1)+1	N*(N–1)+2	…	N*N

Дэвид просит каждого зрителя поставить палец на левую верхнюю картинку (то есть в клетку номер 1), и Магия начинается: маг просит зрителей сдвинуть свой палец K₁ раз в произвольном направлении (сдвигать палец разрешается только на соседнюю картинку по горизонтали или по вертикали, оставлять палец на месте запрещено, при этом если, допустим, Дэвид попросил сдвинуть палец 3 раза, то можно, например, сдвинуть палец на одну клетку вправо, затем — на одну клетку вниз, затем — на одну вверх). Затем со словами "Ваш палец не здесь" Дэвид убирает некоторые картинки, и — что удивительно, пальцы телезрителей действительно не указывают на те картинки, которые убирает Дэвид. Затем он просит сделать K₂ ходов, и так далее (если Дэвид уже убрал какую-то картинку, то ходить через эту клетку нельзя). В конце, Дэвид убирает все картинки, кроме одной, и, улыбаясь, говорит: "Вы здесь" (аплодисменты).

Дэвиду приходится довольно часто повторять этот трюк, и, чтобы не ошибиться, он попросил написать программу, которая будет ему сообщать, сколько ходов должны делать телезрители, и какие картинки нужно убирать. Напишите такую программу.

Входные данные

Во входном файле записано одно число N — размер квадрата (2N100).

Выходные данные

В выходной файл ваша программа должна печатать следующие строки чисел:

K₁ X_1,1 X_1,2 … X_1,_m₁

K₂ X_2,1 X_2,2 … X_2,_m₂

…

K_e X_e_,1 X_e_,2 … X_e_,_me

где K_i — это число ходов, которые должны сделать телезрители, а X_i_,1 … X_i,_mi — номера картинок, которые Дэвид должен убрать с экрана после этого. При этом все K_i должны удовлетворять условию 2NK_i10000 и все K_i должны быть различны. Каждая картинка (кроме той, которая останется) должна убираться ровно один раз. После каждой просьбы зрителей сделать K_i ходов, Дэвид должен убирать хотя бы одну картинку. Каждое K_i должно печататься в начале новой строки. Ситуаций, когда телезритель остался на клетке, у которой нет соседних, а его просят куда-нибудь ходить, возникать не должно.

Примеры

Входные данные

Выходные данные

7 1 3 7 9
9 2 4 6 8

#1040

Кубическое уравнение

Темы: [Целые числа]

Источники: [ Личные олимпиады, Открытая олимпиада школьников, 2005, Задача F ]

Напишите программу, которая будет искать все целые X, удовлетворяющие уравнению

AX³ + BX² + CX + D = 0,

где A, B, C, D — данные целые числа.

Входные данные

Во входном файле записаны четыре целых числа: A, B, C, D. Все числа по модулю не превышают 210⁹.

Выходные данные

В выходной файл выведите сначала количество решений этого уравнения в целых числах, а затем сами корни в возрастающем порядке. Если уравнение имеет бесконечно много корней, выведите в выходной файл одно число –1 (минус один).

Примеры

Входные данные

1 0 0 -27

Выходные данные

1
3

Входные данные

0 1 2 3

Выходные данные

#1041

Скорая помощь

Темы: [Целые числа] [Перебор с отсечением]

Источники: [ Личные олимпиады, Открытая олимпиада школьников, 2005, Задача G ]

Бригада скорой помощи выехала по вызову в один из отделенных районов. К сожалению, когда диспетчер получил вызов, он успел записать только адрес дома и номер квартиры K₁, а затем связь прервалась. Однако он вспомнил, что по этому же адресу дома некоторое время назад скорая помощь выезжала в квартиру K₂, которая расположена в подъезда P₂ на этаже N₂. Известно, что в доме M этажей и количество квартир на каждой лестничной площадке одинаково. Напишите программу, которая вычилсяет номер подъезда P₁ и номер этажа N₁ квартиры K₁.

Входные данные

Во входном файле записаны пять положительных целых чисел K₁, M, K₂, P₂, N₂. Все числа не превосходят 1000.

Выходные данные

Выведите два числа P₁ и N₁. Если входные данные не позволяют однозначно определить P₁ или N₁, вместо соответствующего числа напечатайте 0. Если входные данные противоречивы, напечатайте два числа –1 (минус один).

Примеры

Входные данные

89 20 41 1 11

Выходные данные

2 3

Входные данные

11 1 1 1 1

Выходные данные

0 1

Входные данные

3 2 2 2 1

Выходные данные

-1 -1

#1042

A-функция от строчки

Темы: [Алгоритмы на строках]

Источники: [ Личные олимпиады, Открытая олимпиада школьников, 2005, Задача H ]

Дана строка S, состоящая из N символов. Определим функцию A(i) от первых i символов этой сроки следующим образом:

A(i) = максимально возможному k, что равны следующие строки:

S[1]+S[2]+S[3]+…+S[k]

S[i]+S[i–1]+S[i–2]+…+S[i–k+1]

где S[i] – i-ый символ строки S, а знак + означает, что символы записываются в строчку непосредственно друг за другом.

Напишите программу, которая вычислит значения функции A для заданной строчки для всех возможных значений i от 1 до N.

Входные данные

В первой строке входного файла записано одно число N. 1≤N≤200000. Во второй строке записана строка длиной N символов, состоящая только из больших и/или маленьких латинских букв.

Выходные данные

В выходной файл выведите N чисел — значения функции A(1), A(2), … A(N).

Примеры

Входные данные

5
aabaa

Выходные данные

1 2 0 1 5