Темы
Информатика(2656 задач)
--->
97 задач
<---
#112333
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Заключительный этап,
2014,
1 тур,
Задача C
]
ограничение по времени на тест
5.0 second;
ограничение по памяти на тест
256 megabytes
У Пети на полке стоят n тетрадей с полным собранием его идей. Тетради пронумерованы различными
целыми числами от 1 до \(n\). У Пети есть привычная расстановка тетрадей (возможно, не в порядке нумерации), и он не любит, когда кто-то их переставляет. Петя купил специального Робота, который умеет запоминать
расстановку тетрадей и вычислять число беспорядков в этой расстановке.
Дано \(n\) троек чисел \((a_i, b_i, c_i)\).Требуется найти количество пар индексов \(i < j\) таких, что они равны по ровно одному индексу
Требовалось разместить клетчато-выпуклый многоугольник на поле так, чтобы он занимал как можно меньше плиток размерами \(1 \times k\); Плитки, которые покрываются не полностью, следует учитывать.
Робот считает, что две тетради образуют беспорядок, если тетрадь с меньшим номером стоит правее тетради с большим номером. Например, в расстановке (2; 1; 5; 3; 4) беспорядки образуют три пары тетрадей (2; 1), (5; 3) и (5; 4), поэтому число беспорядков в такой расстановке равно 3.
После ремонта комнаты Петя забыл привычную расстановку своих тетрадей на полке и хочет её восстановить. Робот сохранил её, но он умеет сообщать только число беспорядков в сохраненной расстановке. Петя может попросить Робота поменять местами две тетради в сохраненной расстановке. После такого запроса Робот сохранит новую расстановку и сообщит число беспорядков в ней. Петя может повторять запросы до тех пор, пока не решит, что у него достаточно информации для восстановления привычной расстановки.
Требуется составить программу, которая, общаясь с Роботом, восстанавливает привычную расстановку тетрадей
Протокол взаимодействия
Это интерактивная задача. В процессе тестирования ваша программа будет с использованием стандартных потоков ввода/вывода взаимодействовать с программой жюри, которая моделирует работу Робота.
Сначала ваша программа должна прочитать из стандартного потока ввода два целых числа \(n\) и \(m\) — количество тетрадей Пети и количество беспорядков в его привычной расстановке.
Затем протокол общения вашей программы и программы жюри следующий:
* Для перестановки двух тетрадей ваша программа выводит в стандартный поток вывода запрос в формате: swap \(i\) \(j\), где \(i\) и \(j\) — номера позиций тетрадей, которые Робот должен поменять местами (1 <= \(i\), \(j\) <= \(n\); i != j). После этого она должна считать из стандартного потока ввода одно целое число — количество беспорядков в получившейся расстановке. Ваша программа может сделать не более 300 000 запросов.
* Когда ваша программа сможет восстановить привычную расстановку тетрадей, она должна вывести эту расстановку в формате: answer \(p\), где \(p\) — последовательность из n различных целых чисел в диапазоне от 1 до \(n\), и завершить работу.
Запрос на обмен и вывод привычной расстановки должны завершаться переводом строки и сбросом буфера потока вывода. Для этого используйте flush(output) в Pascal/Delphi; fflush(stdout) или cout.flush() в С/C++.
Система оценки
Данная задача содержит четыре подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за первую подзадачу начисляются только в том случае, если все тесты из этой группы пройдены. Тесты второй, третьей и четвертой подзадач оцениваются по отдельности.
Подзадача 1
1 <= \(n\) <= 100. Подзадача оценивается в 30 баллов.
Подзадача 2
1 <= \(n\) <= 8000. Подзадача оценивается в 20 баллов.
Подзадача 3
1 <= \(n\) <= 60000. Подзадача оценивается в 30 баллов.
Подзадача 4
1 <= \(n\) <= 100000. Подзадача оценивается в 20 баллов.
#112334
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Заключительный этап,
2014,
1 тур,
Задача D
]
ограничение по времени на тест
3.0 second;
ограничение по памяти на тест
256 megabytes
Коллайдер — это установка для изучения столкновений элементарных частиц. При его работе частицы разгоняются до большой скорости. Специальный детектор позволяет фиксировать траектории частиц в виде прямых на горизонтальной плоскости.
На детектор сверху направлена сверхскоростная камера на вращающемся в горизонтальной плоскости креплении. Ориентация камеры в каждый момент времени задаётся направляющей прямой. Камера может сфотографировать произвольную прямоугольную область, одна из сторон которой параллельна заданной направляющей прямой
Для анализа потенциальных столкновений частиц важно, чтобы на каждом фотоснимке были отображены все точки пересечений их траекторий. Камера использует очень дорогие расходные материалы, поэтому площадь каждого фотоснимка необходимо минимизировать.
Требуется написать программу, которая по хронологической последовательности событий двух типов:
• появление новой траектории частицы,
• получение фотоснимка камерой, ориентированной по заданной направляющей прямой,
определит для каждого фотоснимка минимальную площадь прямоугольной области, включающей все точки пересечения траекторий частиц, появившихся до этого снимка.
Формат входного файла
В первой строке входного файла задано одно целое число n (1 <= \(n\) <= 200 000) — общее количество событий. В следующих \(n\) строках заданы описания событий.
Описание каждого события состоит из пяти элементов. Первый элемент является символом «+», если это событие является появлением новой траектории, или символом «?», если это событие является получением фотоснимка. Последующие четыре элемента — целые числа \(x_1\), \(y_1\), \(x_2\), \(y_2\) (−10 000 <= \(x_1\), \(y_1\), \(x_2\), \(y_2\) <= 10 000) — координаты двух несовпадающих точек. Для событий первого типа указанные точки лежат на траектории частицы. Все траектории различны. Для событий второго типа указанные точки лежат на направляющей прямой камеры.
Формат выходного файла
Пусть \(q\) — количество полученных фотоснимков. Выходной файл должен содержать \(q\) вещественных чисел — минимальные возможные площади фотоснимков, перечисленные в порядке их получения камерой.Тест будет успешно пройден, если для каждой из \(q\) выведенных площадей выполняется условие |a - b| / (max(1, b)) <= 10-4, где \(a\) — площадь, выведенная участником, \(b\) — площадь, полученная решением жюри.
Пояснения к примеру
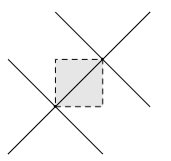
Далее приведены рисунки для первого и второго примеров соответственно.
Система оценивания
Для проверки решений этой задачи используются 50 тестов. Тесты оцениваются независимо. Каждый тест оценивается в 2 балла. Значения \(n\) и \(q\), а также некоторые характеристики тестов приведены в таблице.
| Тест | n | q | Примечание |
| 1. | 10 | 1 | Направляющие прямые параллельны осям координат |
| 2. | 20 | 10 | Направляющие прямые параллельны осям координат |
| 3. | 745 | 365 | Направляющие прямые параллельны осям координат |
| 4. | 1997 | 10 | Направляющие прямые параллельны осям координат |
| 5. | 2000 | 1000 | Направляющие прямые параллельны осям координат |
| 6. | 100001 | 1 | Направляющие прямые параллельны осям координат |
| 7. | 100002 | 1 | Направляющие прямые параллельны осям координат |
| 8. | 200000 | 1 | Направляющие прямые параллельны осям координат |
| 9. | 200000 | 100000 | Направляющие прямые параллельны осям координат |
| 10. | 200000 | 130000 | Направляющие прямые параллельны осям координат |
| 11. | 1000 | 10 | |
| 12. | 500 | 250 | |
| 13. | 10100 | 10000 | |
| 14. | 700 | 100 | |
| 15. | 800 | 71 | |
| 16. | 2001 | 1000 | |
| 17. | 5003 | 2000 | |
| 18. | 7005 | 4000 | |
| 19. | 8007 | 1000 | |
| 20. | 9009 | 4500 | |
| 21. | 90100 | 90001 | |
| 22. | 5000 | 101 | |
| 23. | 6000 | 98 | |
| 24. | 5432 | 2345 | |
| 25. | 9508 | 4079 | |
| 26. | 156002 | 151001 | Все фотоснимки выполняются после появления всех частиц |
| 27. | 157004 | 152001 | Все фотоснимки выполняются после появления всех частиц |
| 28. | 197062 | 190001 | Все фотоснимки выполняются после появления всех частиц |
| 29. | 148008 | 141001 | Все фотоснимки выполняются после появления всех частиц |
| 30. | 169010 | 163501 | Все фотоснимки выполняются после появления всех частиц |
| 31. | 165011 | 159001 | Все фотоснимки выполняются после появления всех частиц |
| 32. | 185001 | 179102 | Все фотоснимки выполняются после появления всех частиц |
| 33. | 176001 | 168098 | Все фотоснимки выполняются после появления всех частиц |
| 34. | 155433 | 147234 | Все фотоснимки выполняются после появления всех частиц |
| 35. | 159608 | 152179 | Все фотоснимки выполняются после появления всех частиц |
| 36. | 165011 | 159001 | |
| 37. | 185001 | 179102 | |
| 38. | 176001 | 174000 | |
| 39. | 155433 | 153556 | |
| 40. | 159608 | 157701 | |
| 41. | 200000 | 1 | |
| 42. | 110000 | 10 | |
| 43. | 120000 | 50 | |
| 44. | 199999 | 70 | |
| 45. | 188888 | 100 | |
| 46. | 200000 | 100000 | |
| 47. | 199999 | 195000 | |
| 48. | 199999 | 100000 | |
| 49. | 178689 | 98276 | |
| 50. | 199998 | 88888 |
Примеры
Входные данные
6 + 0 0 0 1 + 0 0 1 0 + 1 0 0 2 ? 0 0 0 1 + 2 4 3 6 ? 0 0 1 1
Выходные данные
2.0 3.000
Входные данные
7 ? 11 4 -7 8 + -2 -2 1 1 ? 0 0 0 1 + 0 1 1 0 + 0 2 2 0 ? 0 0 0 1 ? 0 0 1 1
Выходные данные
0.0 0.0 0.25 0.0000000
#112335
Темы:
[Обход в глубину]
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Заключительный этап,
2014,
1 тур,
Автомат с игрушками
]
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Заключительный этап,
2014,
1 тур,
Задача A
]
ограничение по времени на тест
3.0 second;
ограничение по памяти на тест
256 megabytes
В развлекательном центре \(Е\)-города был установлен игровой автомат нового поколения. В автомат можно бросить монету и следить за её продвижением сверху вниз по разветвляющемуся лабиринту из трубок. В лабиринте есть n узлов, которые пронумерованы числами
от 1 до \(n\). При бросании монета попадает в первый узел. Каждый узел лабиринта, кроме первого, имеет одну входящую сверху трубку, по которой монета может в него попасть. Из каждого узла выходит не более двух трубок, идущих вниз, одна из которых
ведет налево, а другая — направо. Каждая трубка имеет некоторую ширину. Монета проваливается в более широкую трубку, а в случае равенства ширины трубок — в левую.
После прохождения монеты по трубке ширина этой трубки уменьшается на 1. Монета не может пройти по трубке ширины 0. Если монета достигла узла, из которого она не может дальше двигаться вниз, автомат останавливается и ждёт, когда в него бросят следующую монету
Изначально в каждом узле лабиринта находится по игрушке. Когда монета попадает в узел первый раз, игрушка, находящаяся в этом узле, достаётся игроку, бросившему эту монету.
Панкрату понравилась игрушка, которая находится в узле с номером \(v\).
Требуется написать программу, которая определяет, сколько монет должен бросить в автомат Панкрат, чтобы получить игрушку из узла \(v\).
Формат входного файла
В первой строке входного файла задано число \(n\) — количество узлов в лабиринте. В последующих n строках заданы описания всех узлов, в \(k\)-й из этих строк описан узел с номером \(k\).
Описание k-го узла состоит из четырех целых чисел: \(a_k\), \(u_k\), \(b_k\), \(w_k\). Если из \(k\)-го узла выходит левая трубка, то \(a_k\) — номер узла, в который она ведет (\(k\) < \(a_k\) <= \(n\)), а \(u_k\) — её ширина. Если левой трубки нет, то \(a_k\) = \(u_k\) = 0. Если из \(k\)-го узла выходит правая трубка, то \(b_k\) — номер узла, в который она ведет (\(k\) < \(b_k\) <= \(n\)), а \(w_k\) — её ширина. Если правой трубки нет, то \(b_k\) = \(w_k\) = 0.
В последней строке задано целое число \(v\) (1 <= \(v\) <= \(n\)) — номер узла, в котором находится игрушка, понравившаяся Панкрату.
Гарантируется, что во все узлы, кроме первого, входит ровно одна трубка
Формат выходного файла
Выходной файл должен содержать одно число — количество монет, которое необходимо бросить в автомат Панкрату, чтобы получить игрушку, которая находится в узле \(v\). Если получить выбранную игрушку невозможно, выведите число −1.
Система оценки
Данная задача содержит две подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
Подзадача 1
1 <= \(n\) <= 100
1 <= \(u_k\); \(w_k\) <= 300
Подзадача оценивается в 50 баллов.
Подзадача 2
1 <= \(n\) <= \(10^5\)
1 <= \(u_k\); \(w_k\) <= \(10^9\)
Подзадача оценивается в 50 баллов.
Пояснения к примеру
В первом примере первая монета пройдет лабиринт по следующему пути, и игрок получит игрушки из вершин 1, 3 и 4:
Вторая монета пройдет лабиринт по следующему пути, и игрок получит игрушки из вершин 2 и 6:
Третья монета пройдет лабиринт по следующему пути, и игрок получит игрушки из вершин 5 и 7:
Примеры
Входные данные
7 2 1 3 2 0 0 6 3 4 1 5 1 0 0 0 0 7 2 0 0 0 0 0 0 0 0 0 0 5
Выходные данные
3
Входные данные
4 0 0 2 1 4 1 3 1 0 0 0 0 0 0 0 0 3
Выходные данные
-1
#112815
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Заключительный этап,
2015,
1 тур,
Автоматические друзья
]
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Заключительный этап,
2015,
1 тур,
Задача A
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes
Школа юных программистов решила разработать собственную социальную сеть, которая должна автоматически подбирать для каждого пользователя потенциальных друзей. При регистрации каждому пользователю сети предлагается пройти психологическое тестирование, по результатам которого определяются значения трёх психологических характеристик этого пользователя. Значение каждой характеристики — целое положительное число.
Считается, что если у двух пользователей различаются значения всех трёх психологических характеристик, то они будут постоянно ссориться, а если совпадают значения двух или трёх характеристик, то им будет скучно. Таким образом, потенциальными друзьями являются только такие пары пользователей, у которых совпадают значения ровно одной характеристики, а значения двух других — различаются.
Требуется написать программу, которая по данным \(n\) тройкам (\(a_i , b_i , c_i\)) значений характеристик каждого из пользователей определяет количество пар потенциальных друзей, то есть таких пар индексов \(i < j\), что из трёх равенств \(a_i = a_j , b_i = b_j , c_i = c_j\) выполняется ровно одно.
Входные данные
Первая строка входных данных содержит число \(n\) — количество пользователей. Каждая из последующих \(n\) строк содержит три целых положительных числа \(a_i , b_i и c_i\) — значения характеристик \(i\)-го пользователя
Выходные данные
Выходные данные должны содержать искомое количество пар потенциальных друзей.
Таблица системы оценивания
| Номер подзадачи | Баллы | Ограничения | |
|---|---|---|---|
| \(n\) | \(a_i, b_i, c_i\) | ||
| 1 | 45 | \(1 \leq n \leq 100\) |
\(1 \leq a_i, b_i, c_i \leq 50\) |
| 2 | 55 | \(1 \leq n \leq 100\,000\) | \(1 \leq a_i, b_i, c_i \leq 100\) |
Пояснения к примеру
В первом примере потенциальную пару друзей образуют пользователи 1 и 2, а также 2 и 3. В обоих случаях у пользователей совпадает значение первой характеристики и различаются значения второй и третьей характеристик. Пользователи 1 и 3 имеют одинаковые значения первых двух характеристик, поэтому они не образуют пару потенциальных друзей.
Примеры
Входные данные
3 1 2 3 1 4 5 1 2 4
Выходные данные
2
Входные данные
4 100 100 100 100 100 100 100 99 99 99 99 100
Выходные данные
5
#112816
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Заключительный этап,
2015,
1 тур,
Задача B
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes
Одна из центральных площадей Архангельска замощена прямоугольными плитками размера \(1 \times k\). Если ввести систему координат, так что левый нижний угол одной из плиток будет иметь координаты (0, 0), то левые нижние углы плиток будут иметь координаты (\(i · k + j, j\)) для всех целых \(i\) и \(j\).
На площади было решено установить памятник известному архангельскому писателю и художнику Степану Писахову. Для установки памятника необходимо удалить все плитки, полностью или частично попадающие под его основание. Основание памятника имеет форму многоугольника с целочисленными координатами вершин, все стороны которого параллельны осям координат. Известно, что любая прямая, пересекающая основание памятника и параллельная одной из осей координат, в пересечении с основанием образует один отрезок.
Для установки памятника необходимо выбрать место на площади таким образом, чтобы количество удалённых плиток было минимальным. При выборе места основание разрешается только передвигать параллельно осям координат.
Требуется написать программу, вычисляющую минимальное количество плиток, которые придётся удалить.
Входные данные
Первая строка входных данных содержит два числа \(n\) и \(k\) — количество вершин в основании памятника и размер плитки.
Каждая из последующих \(n\) строк содержит два целых числа \(x_i\) , \(y_i\) — координаты \(i\)-й вершины основания. Координаты перечислены в порядке обхода против часовой стрелки.
Выходные данные
Единственная строка выходных данных должна содержать минимально возможное количество плиток, которые необходимо удалить для размещения памятника на площади.
Таблица системы оценивания
Замечание
Примеры
Входные данные
12 3 2 3 1 3 1 2 3 2 3 1 8 1 8 2 10 2 10 3 8 3 8 4 2 4
Выходные данные
7
Выбрано
:
|