--->
10 задач
<---
#1340
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Заключительный этап,
2009,
Задача D
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
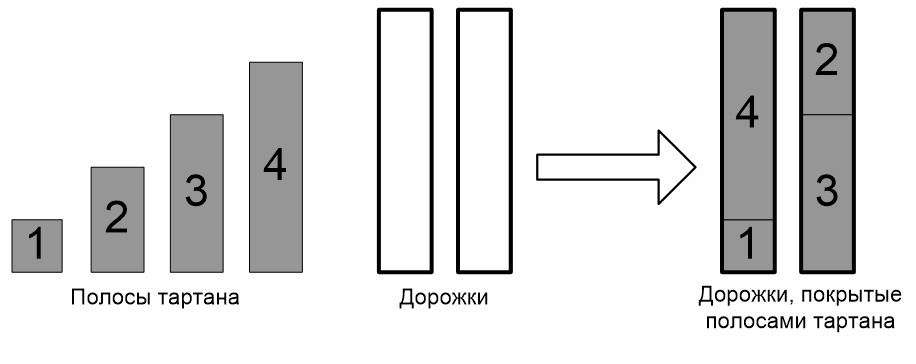
В стране Флатландия решили построить легкоатлетический манеж с M одинаковыми прямолинейными беговыми дорожками. Они будут покрыты полосами из синтетического материала пружинкин. На складе имеются N полос пружинкина, длины которых равны 1, 2, …, N метров соответственно (i-я полоса имеет длину i метров).
Было решено использовать все полосы со склада, что определило длину дорожек манежа. Полосы пружинкина должны быть уложены без перекрытий и промежутков. Разрезать полосы на части нельзя. Полосы укладываются вдоль дорожек, ширина полосы пружинкина совпадает с шириной беговой дорожки.
Требуется написать программу, которая определяет, можно ли покрыть всем имеющимся материалом M дорожек, и если это возможно, то распределяет полосы пружинкина по дорожкам.
Входные данные
Во входном файле содержатся два целых числа, разделенных пробелом: M — количество дорожек и N — количество полос пружинкина (1 ≤ M ≤ 1000, 1 ≤ N ≤ 30000).
Выходные данные
В случае, если распределить имеющиеся полосы пружинкина на M дорожек одинаковой длины невозможно, то в выходной файл выведите слово «NO».
В противном случае, в первую строку выведите слово «YES». В последующих M строках дайте описание использованных полос для каждой дорожки в следующем формате: сначала целое число t — количество полос на дорожке, затем t целых чисел — длины полос, которые составят эту дорожку. Если решений несколько, можно вывести любое из них.
В задаче есть группа на первые 17 тестов и она оценивается в 20 баллов. затем идёт потестовая оценка по 2 балла за пройденный тест.
Примеры входных и выходных данных
| Ввод | Вывод |
| 2 4 | YES 2 1 4 2 3 2 |
| 3 4 | NO |
#1341
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Заключительный этап,
2009,
Задача E
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Около прямолинейного забора, состоящего из N одинаковых бетонных плит, проводится конкурс граффити, в котором участвуют M граффити-художников. Художники должны разрисовать все плиты своими произведениями за наименьшее возможное время.
Плиты пронумерованы числами от 1 до N, граффити-художники имеют номера от 1 до M. Первоначально i-й граффити-художник находится около плиты с заданным номером pi. Каждому художнику требуется b минут на разрисовывание любой плиты. Каждую плиту должен разрисовать ровно один граффити-художник.
В начале работы, а также после разрисовывания любой плиты граффити-художник может перейти к любой неразрисованной плите. Время перемещения граффити-художника от любой плиты к соседней с ней одинаково и равно a минут. Таким образом, чтобы перейти от плиты с номером i к плите с номером j художнику требуется a×|i – j| минут.
Требуется написать программу, которая поможет участникам конкурса разрисовать все плиты за минимальное возможное время.
Входные данные
В первой строке входного файла указаны числа N — количество плит в заборе и M — количество граффити-художников (1 ≤ N, M ≤ 100000). Во второй строке заданы два целых числа: a — количество минут, которое требуется для перехода от любой плиты к соседней, и b — количество минут, которое требуется граффити-художнику на разрисовывание одной плиты (1 ≤ a, b ≤ 106). В третьей строке заданы M чисел p1, p2, …, pM — начальные положения граффити-художников (1 ≤ pi ≤ N).
Выходные данные
В первую строку выходного файла выведите минимальное количество минут, требуемых художникам для выполнения работы.
В последующих M строках выведите описание действий художников. В i-й из этих строк должно содержаться описание действий i-го художника: количество плит, которые должен разрисовать этот художник, и номера этих плит в очередности их разрисовывания. Если оптимальных решений несколько, можно вывести любое из них.
Примечание
Решения, корректно работающие при M ≤ 2, будут оцениваться из 40 баллов.
Примеры
Входные данные
10 2 19 56 9 2
Выходные данные
375 5 10 9 8 7 6 5 1 2 3 4 5
#2531
Темы:
[Быстрая сортировка]
[Жадный алгоритм]
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Заключительный этап,
2010,
Задача C
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Есть \(n\) человек, которые хотят улететь из Москвы в Ханты-Мансийск. Каждый день летает один самолёт вместимостью \(k\) человек. У каждого человека есть множество дней, когда он может улететь, — отрезок \([a_i,b_i]\). Нужно придумать такое распределение людей по самолётам, что до Ханты-Мансийска долетит максимальное число людей. Среди людей есть участники РОИ, которых нужно перевезти обязательно (остальных людей будем называть обычными).
В связи с проведением в Ханты-Мансийске Всероссийской олимпиады школьников по информатике агентство авиаперевозок обязано перевезти самолётами всех участников олимпиады. Всего за \(m\) дней, пронумерованных от 1 до \(m\), из Москвы в Ханты-Мансийск хотят вылететь \(n\) пассажиров, в том числе и участники олимпиады.
Все желающие вылететь в Ханты-Мансийск заполнили анкеты, в которых указали информацию о возможных днях вылета и об участии в олимпиаде. Информация о возможных днях вылета
Самолёт из Москвы в Ханты-Мансийск вылетает всего один раз в день и вмещает не более \(k\) пассажиров. Необходимо распределить пассажиров по дням вылета таким образом, чтобы улетело как можно большее количество пассажиров, при этом все участники Всероссийской олимпиады должны улететь обязательно.
Напишите программу, определяющую распределение пассажиров по дням вылета, при котором максимизируется количество перевезённых пассажиров, или определяющую, что такого распределения не существует.
Входные данные
В первой строке входного файла записаны три натуральных числа — \(n\), \(m\) и \(k\) (\(1\le n\le100\,000\), \(1\le m\le100\,000\), \(1\le k\le100\,000\)). Далее следуют \(n\) строк,
Выходные данные
В первой строке выходного файла выведите максимальное количество пассажиров \(l\), которых можно перевезти из Москвы в Ханты-Мансийск. Если невозможно выполнить поставленную задачу, то в первой строке необходимо вывести число 0. В случае положительного ответа выведите во второй строке n чисел, а именно, для каждого пассажира выведите номер дня, в который запланирован его вылет, либо 0, если этому пассажиру не нашлось места в оптимальном распределении. Числа во второй строке разделяйте пробелами. Если оптимальных распределений несколько, выведите любое из них.
Система оценивания
Примеры
Входные данные
3 2 1 1 2 1 1 2 0 1 2 1
Выходные данные
2 1 0 2
Входные данные
3 4 1 1 2 1 1 3 1 1 4 0
Выходные данные
3 1 2 3
Входные данные
10 4 2 2 3 0 2 3 0 1 3 1 3 4 0 3 4 1 2 3 0 2 2 0 1 3 1 4 4 0 2 4 0
Выходные данные
8 2 3 1 4 4 3 2 1 0 0
#3394
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Заключительный этап,
2011,
Задача B
]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes
Для подготовки к чемпионату мира по футболу 2018 года создается школа олимпийского резерва. В нее нужно зачислить \(M\) юношей 1994−1996 годов рождения. По результатам тестирования каждому из \(N\) претендентов был выставлен определенный балл, характеризующий его мастерство. Все претенденты набрали различные баллы. В составе школы олимпийского резерва хотелось бы иметь \(A\) учащихся 1994 г.р., \(B\) – 1995 г.р. и \(C\) – 1996 г.р. (\(A + B + C = M\)). При этом минимальный балл зачисленного юноши 1994 г.р. должен быть больше, чем минимальный балл зачисленного 1995 г.р., а минимальный балл зачисленного 1995 г.р. должен быть больше, чем минимальный балл зачисленного 1996 г.р. Все претенденты, набравшие балл больше минимального балла для юношей своего года рождения, также должны быть зачислены.
В базе данных для каждого претендента записаны год его рождения и тестовый балл. Требуется определить, сколько нужно зачислить юношей каждого года рождения \(M_{94}\), \(M_{95}\) и \(M_{96}\) (\(M_{94} + M_{95} + M_{96} = M\)), чтобы значение величины \(F = |M_{94} − A| + |M_{95} − B| + |M_{96} − C|\) было минимально, все правила, касающиеся минимальных баллов зачисленных, были соблюдены, и должен быть зачислен хотя бы один юноша каждого требуемого года рождения.
Входные данные
В первой строке входного файла находится число \(K\) – количество наборов входных данных. Далее следуют описания каждого из наборов. В начале каждого набора расположены три натуральных числа \(A\), \(B\), \(C\). Во второй строке описания находится число \(N\) – количество претендентов (гарантируется, что \(N \geq A + B + C\)). В каждой из следующих \(N\) строк набора содержатся два натуральных числа – год рождения (число 1994, 1995 или 1996 соответственно) и тестовый балл очередного претендента.
Выходные данные
Ответ на каждый тестовый набор выводится в отдельной строке. Если хотя бы одно из требований выполнить невозможно, то в качестве ответа следует вывести только число −1. В противном случае соответствующая строка сначала должна содержать минимальное значение величины \(F\), а затем три числа \(M_{94}\), \(M_{95}\) и \(M_{96}\), на которых это минимальное значение достигается, удовлетворяющие всем требованиям отбора. Если искомых вариантов несколько, то разрешается выводить любой из них.
Комментарий
В первом примере на первом наборе ответ не существует, потому что нельзя пригласить хотя бы одного юношу 1995 г.р. Во втором наборе ответ существует и единственный, в третьем – нельзя выполнить правило относительно минимальных баллов.
Во втором примере правильным является также ответ 2 2 2 2.
Подзадачи и система оценки
Данная задача содержит три подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
Подзадача 1 (25 баллов)
\(K = 1\); \(N \leq 100\); каждый претендент характеризуется своим баллом от 1 до \(N\).
Подзадача 2 (25 баллов)
Сумма значений \(N\) по всем тестовым наборам не превосходит 10 000, каждый претендент характеризуется своим баллом от 1 до \(10^9\).
Подзадача 3 (25 баллов)
Сумма значений \(N\) по всем тестовым наборам не превосходит 100 000, каждый претендент характеризуется своим баллом от 1 до \(N\).
Подзадача 4 (25 баллов)
Сумма значений \(N\) по всем тестовым наборам не превосходит 300 000, каждый претендент характеризуется своим баллом в диапазоне от 1 до \(10^9\).
Примеры
Входные данные
3 1 1 1 4 1994 3 1994 4 1996 1 1996 2 1 1 1 3 1995 2 1994 3 1996 1 1 1 1 3 1994 1 1995 2 1996 3
Выходные данные
-1 0 1 1 1 -1
Входные данные
1 2 3 1 7 1996 2 1994 7 1994 4 1996 1 1995 3 1994 5 1995 6
Выходные данные
2 3 2 1
#3397
Темы:
[Жадный алгоритм]
[Задачи на моделирование]
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Заключительный этап,
2011,
Задача E
]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes
В городе \(\pi\) недавно построили парк аттракционов, в котором есть павильон игровых автоматов. Каждый из автоматов рассчитан на одного человека. В программе Всероссийской олимпиады планируется посещение этого павильона.
Перед организаторами встала сложная задача — составить расписание игры участников олимпиады на автоматах таким образом, чтобы каждый из \(N\) участников олимпиады смог поиграть на каждом из автоматов, и при этом автобус, увозящий участников из парка олимпиады, смог бы отправиться к месту проживания как можно раньше.
Время перемещения участников между автоматами, а также между автобусом и павильоном считается равным нулю. Каждый из участников в любой момент времени может как играть на автомате, так и ждать своей очереди, например, гуляя по парку. Для каждого из \(M\) (\(M \leq N\)) автоматов известно время игры на нём \(t_i\) (\(1 \leq i \leq M\)). Прервать начатую игру на автомате невозможно. Автобус привозит всех участников олимпиады в парк одновременно в нулевой момент времени.
Требуется написать программу, которая по заданным числам \(N\), \(M\) и \(t_i\) определяет оптимальное расписание игры на автоматах для каждого из участников.
Входные данные
В первой строке входного файла содержатся два числа: \(N\) и \(M\) (\(1 \leq M \leq N \leq 100\)). Во второй строке заданы \(M\) целых чисел \(t_i\) (\(1 \leq t_i \leq 100\)), каждое из которых задаёт время игры на \(i\)-м автомате (\(1 \leq i \leq M\)). Числа в строке разделяются одиночными пробелами.
Выходные данные
В первой строке необходимо вывести одно число — минимально возможное время отправления автобуса из парка аттракционов. Далее необходимо вывести \(N\) расписаний игр на автоматах, по одному для каждого из участников. Каждое расписание описывается в (\(M + 1\)) строках, первая из которых — пустая, а далее следуют \(M\) строк, описывающих автоматы в порядке их посещения этим участником. Посещение автомата описывается двумя целыми числами: номером автомата \(j\) (\(1 \leq j \leq M\)) и временем начала игры участника на этом автомате.
Примеры тестов
Подзадачи и система оценки
Данная задача содержит пять подзадач. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
Подзадача 1 (20 баллов)
\(M = 1\), \(1 \leq N \leq 100\), \(t_1\) лежит в пределах от 1 до 100.
Подзадача 2 (20 баллов)
Все \(t_i\) равны 1, \(N = M\).
Подзадача 3 (20 баллов)
Все \(t_i\) равны 1, \(N > M\).
Подзадача 4 (20 баллов)
Числа \(t_i\) лежат в пределах от 1 до 100, \(N = M\).
Подзадача 5 (20 баллов)
Числа \(t_i\) лежат в пределах от 1 до 100, \(N > M\).
Примеры
Входные данные
2 1 2
Выходные данные
4 1 0 1 2
Входные данные
3 2 2 1
Выходные данные
6 1 0 2 2 1 2 2 4 2 0 1 4
Выбрано
:
|