--->
6 задач
<---
Источники
#1049
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Заключительный этап,
2004,
1 день,
Задача C
]
ограничение по времени на тест
0.5 second;
ограничение по памяти на тест
64 megabytes
Горнолыжник, готовясь к соревнованиям, нарисовал на бумаге схему горнолыжной трассы для выбора оптимального маршрута спуска. На схеме расположенные на трассе ворота представлены горизонтальными отрезками. Никакая пара ворот не имеет общих точек.
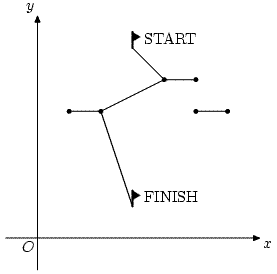
Маршрут должен представлять собой ломаную, начинающуюся в точке старта на вершине горы и заканчивающуюся в точке финиша у ее подножия. Маршрут выбирается таким образом, что y-координата каждой следующей вершины ломаной оказывается строго меньше y-координаты предыдущей вершины. Один из возможных маршрутов представлен на рисунке.
За каждые ворота, через которые не проходит маршрут, лыжнику начисляются штрафные очки. Общий штраф за спуск по маршруту вычисляется как сумма длины маршрута и штрафных очков за непройденные ворота.
Требуется написать программу, которая определяет, какой минимальный общий штраф горнолыжник может получить при прохождении трассы.
Входные данные
В первой строке входного файла задано число N - количество ворот на трассе (0 ≤ N ≤ 500), в следующих двух строках заданы Sx, Sy, Fx, Fy - координаты точек старта и финиша соответственно. В каждой из следующих N строк записаны четыре числа ai, bi, yi, ci - x-координаты левого и правого концов ворот, y-координата ворот и штраф за непрохождение данных ворот (ai < bi, Fy < yi < Sy, ci - целое число, 0 ≤ ci ≤ 10000). Все координаты - целые числа, не превосходящие по модулю 10000.
Выходные данные
В выходной файл выведите наименьший возможный общий штраф за прохождение трассы с точностью не менее 4 знаков после десятичной точки.
Система оценки
Потестовая.
Примеры
Входные данные
4 3 6 3 1 5 7 4 1 4 5 5 10 1 2 4 5 2 5 2 0
Выходные данные
7.8126
ограничение по времени на тест
0.5 second;
ограничение по памяти на тест
64 megabytes
В области Тампере существуют станции обслуживания мобильных телефонов четвертого поколения, которые работают следующим образом. Вся область разделена на квадраты. Квадраты формируют матрицу S×S, строки и столбы которой нумеруются с 0 до S - 1. Каждый квадрат содержит одну станцию обслуживания. Количество активных мобильных телефонов внутри квадрата может меняться, потому что телефон может перемещаться из одного квадрата в другой или выключаться. Временами каждая станция обслуживания передает сведения об изменении в количестве активных телефонов на главную станцию обслуживания (вместе с номером строки и столбца матрицы).
Напишите программу, которая принимает эти сведения и отвечает на запросы о текущем количестве активных мобильных телефонов в любой прямоугольной области.
Входные данные
Каждый запрос к программе описывается на отдельной строке и состоит из одного целого числа, описывающего команду, а также из дополнительных параметров команды в соответствии со следующей таблицой:
| Команда | Параметры | Значение |
|---|---|---|
| 0 | S | Инициализирует матрицу размером S×S, состоящую только из нулей. Эта команда поступает один раз и является самой первой командой. |
| 1 | X Y A | Добавить число A к количеству активных мобильных телефонов в квадрате (X;Y). Число A может быть как положительным, так и отрицательным. |
| 2 | L B R T | Выдать текущую сумму количеств активных мобильных телефонов во всех квадратах (X;Y), где L ≤ X ≤ R, B ≤ Y ≤ T. |
| 3 | Прервать программу. Эта команда поступает один раз и является самой последней командой. |
Все значения всегда лежат в правильном диапазоне, поэтому нет необходимости их проверять. В частности, если число A отрицательное, то число активных телефонов в каком-либо квадрате все равно не станет меньше нуля. Индексы начинаются с 0, поэтому, например, для таблицы размера 4×4 имеем 0 ≤ X ≤ 3, 0 ≤ Y ≤ 3.
Выходные данные
Ваша программа не должна отвечать ни на какую команду, кроме 2. Если команда 2, то ваша программа должна вывести единственную строку, содержащую одно целое число — ответ на этот запрос.
Ограничения
| Размер таблицы | S×S | 1×1 ≤ S×S ≤ 1024×1024 |
| Значение ячейки в любой момент времени | V | 0 ≤ V ≤ 215 - 1 (= 32767) |
| Величина обновления | A | -215 ≤ A ≤ 215 - 1 (= 32767) |
| Количество команд | U | 3 ≤ U ≤ 60002 |
| Максимальное количество активных телефонов во всей таблице | M | M = 230 |
Примеры
Входные данные
0 4 1 1 2 3 2 0 0 2 2 1 1 1 2 1 1 2 -1 2 1 1 2 3 3
Выходные данные
3 4
#112776
Темы:
[Дерево Фенвика]
[Перестановки]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes
Феоктист Всеволодович — преподаватель физкультуры старой закалки, глубоко убеждённый, что в начале каждого урока школьников необходимо построить по росту. Для этого он сначала просит школьников построиться самостоятельно, после чего последовательно меняет местами произвольную пару стоящих рядом учеников, пока шеренга не примет желанный вид.
Всего на урок пришло \(N\) детей, изначально построившихся таким образом, что рост стоящего на позиции \(i\) равен \(h_i\) (используется нумерация c \(1\)). Можно считать, что все числа \(h_i\) различны и лежат в диапазоне от 1 до \(N\). Шеренга считается упорядоченной, если на первой позиции стоит школьник ростом один, на второй позиции стоит школьник ростом два и так далее.
Феоктист Всеволодович получает большое удовольствие от процесса упорядочивания школьников, поэтому он всегда выбирает наиболее длинную последовательность обменов. С другой стороны, он не хочет чтобы ученики догадались о том, что он умышленно затягивает построение, поэтому никогда не делает заведомо бессмысленных обменов. А именно, преподаватель никогда не меняет местами школьников на позициях \(i\) и \(j\), если \(h_i < h_j\) . Очевидно, что данное ограничение делает процесс сортировки шеренги по росту конечным.
Староста Саша очень любит играть в волейбол и прекрасно понимает, что чем дольше преподаватель будет расставлять всех по местам, тем меньше времени останется для игры. Ученики уже построились некоторым образом, а Феоктист Всеволодович вышел поговорить по телефону, так что Саша может успеть поменять местами ровно двух школьников, необязательно стоящих рядом в шеренге. Разумеется, он хочет сделать это таким образом, чтобы преподаватель как можно быстрее закончил упорядочивать шеренгу (Саша давно уже раскусил, как именно действует Феоктист Всеволодович). С информатикой у старосты всегда были определённые проблемы, поэтому ему требуется ваша помощь.
Входные данные
В первой строке ввода содержится единственное число N — количество школьников на уроке (\(1 \le N \le 1 000 000\)).
Во второй строке записано \(N\) различных целых чисел \(h_i\) (\(1 \le h_i \le N\)). \(i\)-е число соответствует росту школьника стоящего на \(i\)-й позиции
Выходные данные
Выведите два числа — номера позиций школьников, которым необходимо поменяться местами, чтобы минимизировать количество действий преподавателя. Если таких пар несколько, то выведите любую из них. Если никому меняться местами не нужно, выведите -1 -1
Замечание
В первом примере из условия после Сашиной перестановки, получится последовательность {2, 1, 3, 5, 4}, и тренер сможет сделать всего два обмена, перед тем как последовательность станет упорядоченной (например, он может поменять местами 1-го и 2-го школьника, а затем 4-го и 5-го). Если Саша поменяет местами двух других школьников, тренер затем сможет сделать три или более обменов.
Система оценки
Тесты к этой задаче состоят из одиннадцати групп. Баллы за каждую группу тестов ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.
Примеры
Входные данные
5 2 4 3 5 1
Выходные данные
2 5
Входные данные
4 1 2 3 4
Выходные данные
-1 -1
Входные данные
10 2 3 7 1 5 10 4 6 9 8
Выходные данные
3 7
#113556
Темы:
[Дерево отрезков, RSQ, RMQ]
[Дерево Фенвика]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Юный Мирко решил купить куклу вуду. Учитывая что он крайне заинтересован в том, ктобы купить ее как можно дешевле, он начал отслеживать цены на кукол вуду каждый день. Его список состоит из цен на куклы в последние N дней, где a i обозначает цену куклы i дней назад.
Мирко думает, что нашел связь между средней ценой кукол в течении нескольких последовательных дней и ценой куклы в следующий день. Он хочет проверить свою догадку и задался вопросом: "Для данного числа P , сколько существует наборов последовательных дней в течении последних N дней, для которых средняя цена куклы в эти дни составляет не менее P ".
Два набора последовательных дней считаются различными, если у них отличается первый или последний день.
Входные данные
Первая строка содержит одно целое число N ( 1 ≤ N ≤ \(10^6\) ), количество дней в списке Мирко. Вторая строка содержит N целых чисел a i ( 0 ≤ a i ≤\(10^9\) ) - цены кукол в соответствующие дни. Третья строка содержит одно целое число P ( 0 ≤ P ≤\(10^9\) ).
Выходные данные
Выведите одно целое число - ответ на вопрос Мирко для данного P .
Примеры
Входные данные
3 1 2 3 3
Выходные данные
1
Входные данные
3 1 3 2 2
Выходные данные
5
Входные данные
3 1 3 2 3
Выходные данные
1
|
Я на выборы никогда не ходил, но в этот раз точно пойду за Зигги голосовать. Кандидат от народа!
Вдохновившись трудами греческих философов, Спортакус решил избрать главу правительства в Лентяево. Поскольку греческие философы убедили Спортакуса, что демократия является лучшим видом государственного устройства, он решил провести выборы. Для этого он открыл n избирательных участков, пронумерованных от 1 до n . Известно, что на участке с номером i проголосовали a i жителей Лентяево.
После окончания выборов Спортакус решил подвести некоторую статистику явки на выборах. Спортакус знает множество разных статитстических величин, но наиболее показательной он считает k -ю порядковую статистику, поэтому для некоторых регионов и некоторых значений k Спортакус хочет узнать значение k -й порядковой статистики явок на участках данного региона.
Опишем действия Спортакуса более формально. Регионом с границами l и r Спортакус называет множество избиртельных участков, чьи номера лежат на промежутке от l до r включительно. k -й порядковой статистикой массива чисел супергерой называет число, которое бы находилось на k -й позиции в этом массиве, если бы он был упорядочен по возрастанию.
Стефани огорчает, что явка на выборах не соотетствует её ожиданиям, поэтому она решила слегка изменить значения явок на некоторых участках так, чтобы выборы казались более успешными. Для этого она выбирает четыре числа l , r , x и y и на всех избирательных участках региона с границами l и r , на которых явка равна x меняет протокол, после чего явка на этих участках становится равной y .
Напишите программу, отвечающую на запросы Спортакуса с учётом изменений, которые делает Стефани.
Входные данные
В первой строке содержатся два целых числа n и m ( 1 ≤ n , m ≤ 100 000 ) — количество избирательных участков и количество событий.
Во второй строке содержатся n целых чисел ( 1 ≤ a i ≤ n ) — количество людей, проголосовавших на участке с номером i .
В следующих m строках содержатся описания событий. Каждое событие задано в одном из двух форматов.
1 l r x y ( 1 ≤ l ≤ r ≤ n , 1 ≤ x , y ≤ n ) обозначает, что Стефани на всех участках региона с границами l и r и явкой x установила явку равной y .
2 l r k ( 1 ≤ l ≤ r ≤ n , 1 ≤ k ≤ r - l + 1 ) обозначает, что Спортакуса интересует значение k -й порядковой статистики явок на участках в регионе с границами l и r .
Выходные данные
Для каждого вопроса Спортакуса выведите ответ на него.
Система оценки
Группа 1 (10 баллов) 1 ≤ n , m ≤ 100 . Для прохождения этой подгруппы требуется прохождение тестов из условия.
Группа 2 (10 баллов) 1 ≤ n ≤ 5000, 1 ≤ m ≤ 100 000 , нет запросов первого типа. Для прохождения этой подгруппы требуется прохождение тестов из условия.
Группа 3 (10 баллов) 1 ≤ n , m ≤ 100 000 , нет запросов первого типа. Для прохождения этой подгруппы требуется прохождение группы 2.
Группа 4 (20 баллов) 1 ≤ n , m ≤ 100 000 , в запросах первого типа l = r . Для прохождения этой подгруппы требуется прохождение группы 3.
Группа 5 (50 баллов) Без дополнительных ограничений. Для прохождения этой подгруппы требуется прохождение всех предыдущих групп.
Примеры
Входные данные
3 3 2 3 3 2 1 3 1 1 1 3 3 1 2 1 3 2
Выходные данные
2 1
Выбрано
:
|