#3787

Кривая дракона

Темы: [Арифметические алгоритмы] [Цикл for]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Московская область, Очный этап, 2011, Задача B ]

Сегодня мальчик Саша на уроке математики узнал про фракталы. Учитель показывал так называемую «кривую дракона». Она представляет собой геометрическую фигуру, которая строится следующим образом: на первом шаге проводится отрезок из начала координатной плоскости в точку (0; 1). Далее на каждом шаге из конца фрактала повторяется уже нарисованная часть фигуры, повернутая на 90 градусов против часовой стрелки (см. рисунок).

После уроков Саша попробовал сам изобразить «кривую дракона», и теперь он хочет знать, в какой точке координатной плоскости он закончил рисовать фрактал, проделав описанные выше N шагов. Требуется написать программу, которая по заданному числу N определяет координаты конца фрактала после выполнения N шагов.

$\text{[math]}$

Входные данные

Вводится одно целое число N (1 ≤ N ≤ 30).

Выходные данные

Выведите два числа через пробел — координаты конца фрактала.

Примеры

Входные данные

Выходные данные

1 1

Входные данные

Выходные данные

2 -2

#3788

Кубики

Темы: [Одномерные массивы]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Московская область, Очный этап, 2011, Задача C ]

ООО «Симптотика» собирается наладить выпуск обучающих игр для детей младшего дошкольного возраста. Одной из придуманных игр был набор кубиков, из которых можно было собирать различные фигуры. Кубики упаковывались в коробку размером N × N × 1 кубиков.

Однако, многочисленные маркетинговые исследования показали, что детям неинтересно просто собирать различные фигурки. Гораздо интереснее складывать некоторый набор кубиков на дно коробки в столбики, а после этого переворачивать коробку на 90 градусов по часовой стрелке и смотреть, как именно меняется их расположение. Будем для простоты считать, что коробка поворачивается мгновенно, после чего все кубики падают на дно. На следующем рисунке продемонстрировано, как выглядит расположение кубиков в коробке до и после поворота на 90 градусов.

$\text{[math]}$

Разумеется, многим детям становится интересно, как будет выглядеть расположение кубиков после K поворотов в том же направлении. Требуется написать программу, которая вычисляет итоговое положение кубиков в коробке после K поворотов.

Входные данные

Сначала вводятся целые числа N и K (1 ≤ N ≤ 10, 0 ≤ K ≤ 10⁹). После этого, во второй строке вводятся N неотрицательных чисел, не превышающих N. i-ое число обозначает количество кубиков в столбце под номером i.

Выходные данные

Необходимо вывести N чисел через пробел, i-ое из которых обозначает количество чисел в i-ом столбце в полученном после K поворотов расположении кубиков.

Примечание

Пример соответствует иллюстрации из условия.

Примеры

Входные данные

5 1
1 3 4 0 1

Выходные данные

4 2 2 1 0

#3789

Сохранить энергию

Темы: [Динамическое программирование: два параметра]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Московская область, Очный этап, 2011, Задача D ]

Одна Фруктовая Компания, производящая электронику, решила озаботиться длительностью работы своих смартфонов от аккумулятора.

Выяснилось, что процессор, который они закупают у азиатского поставщика, поддерживает m различных режимов работы, при этом каждая из k операций языка программирования (который Фруктовая Компания использует для написания всех своих программ) может быть выполнена в каждом из режимов. Одновременно процессор может работать только в одном режиме, но перед выполнением каждой из операций можно один раз переключиться в любой другой режим работы.

Известно количество единиц энергии, которое тратится для исполнения каждой из операций в каждом режиме, а также сколько энергии тратится на переключение между режимами. Требуется написать программу, определяющую, какое минимальное количество энергии необходимо потратить для выполнения заданной программы.

В начале выполнения программы процессор находится в первом режиме, завершиться выполнение программы может при любом режиме процессора.

Входные данные

Первая строка содержит три целых числа: число k (1 ≤ k ≤ 100) — количество операций в языке программирования, число m (1 ≤ m ≤ 100) — количество режимов работы, которое поддерживает процессор, и число n (1 ≤ n ≤ 10000) — количество операций в исследуемой программе.

Следующие k строчек содержат по m целых неотрицательных чисел, не превышающих 100. j-е число в i-ой строчке обозначает, сколько энергии тратится на выполнение i-ой операции в j-ом режиме команд.

Далее следует m строчек, содержащих по m целых неотрицательных чисел, не превышающих 100. j-ое число в i-ой строчке обозначает, сколько единиц энергии тратится на переключение процессора с режима i на режим j. Гарантируется, что в i-ой строке i-ое число равно 0.

Последняя строчка содержит исследуемую программу: n натуральных чисел, не превышающих k и соответствующих операциям языка программирования.

Выходные данные

Выведите одно число — минимальное количество единиц энергии, необходимое для выполнения программы.

Подзадачи и система оценки

Тесты к этой задаче состоят из трех групп.

Тесты из условия, оцениваются в ноль баллов.
В тестах этой группы $n$, $m$, $k$ не превосходят 10. Эта группа оценивается в 50 баллов, баллы ставятся только при прохождении всех тестов группы.
В тестах этой группы $m$ не превосходит 10. Эта группа оценивается в 30 баллов, баллы ставятся только при прохождении всех тестов группы и предыдущих групп.
В тестах этой группы дополнительные ограничения отсутствуют. Группа оценивается в 20 баллов, баллы ставятся только при прохождении всех тестов этой и предыдущих групп.

Примеры

Входные данные

Выходные данные

Входные данные

Выходные данные

#3854

Fruit Slice

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Московская область, Интернет этап, 2011, Задача A ]

Правила игры Fruit Slice для сенсорных мобильных телефонов очень просты. В течение некоторого времени на экране появляются фрукты, а игрок должен провести пальцем по экрану так, чтобы линии, проведенные им, пересекли как можно больше фруктов. В случае, если линия пересекает фрукт, он разрезается на две половинки, а игрок получает очки следующим образом:

за разрезание большого фрукта игрок получает два очка, за разрезание маленького — три;
если одной линией игрок разрезал три фрукта, то помимо очков, полученных за каждый фрукт по отдельности, он получает еще 5 бонусных очков;
если одной линией игрок разрезал 4 и более фруктов, то помимо очков, полученных за каждый фрукт по отдельности, он получает еще 10 бонусных очков.

Вася поиграл в игру и набрал суммарно P очков, при этом N раз получив 5 бонусных очков и M раз получив 10 бонусных очков. Теперь ему интересно, какое минимальное количество фруктов можно разрезать согласно правилам этой игры, чтобы добиться такого же результата.

Входные данные

В единственной строке вводятся три числа P, N и M (0 ≤ P ≤ 10⁹, 0 ≤ N, M ≤ 10⁶).

Выходные данные

Выведите одно число — минимальное количество фруктов, которое нужно разрезать, чтобы добиться указанного результата. Гарантируется, что входные данные корректны, то есть существует такой набор фруктов, что возможно набрать суммарно P очков, при этом N раз получив 5 бонусных очков и M раз получив 10 бонусных очков.

Примечание

В первом примере добиться указанного результата можно, разрезав 5 маленьких фруктов и 1 большой. При этом у игрока есть возможность получить 5 бонусных очков, разрезав какие-то три фрукта одной линией.

Во втором примере добиться указанного результата можно, разрезав одной линией 3 больших фрукта и 1 маленький. Обратите внимание, что поскольку Вася один раз получил 10 бонусных очков, он не может добиться указанного результата, разрезав менее 4-х фруктов.

Система оценки

Тесты в этой задаче разбиты на группы. Баллы начисляются только за группу целиком в том случае, когда пройдены все тесты группы, а также все тесты предыдущих групп.

Тесты 1–2. Тесты из условия, оцениваются в 0 баллов.
Тесты 3–5. $P \le 30$, $N, M \le 1$, оцениваются в 30 баллов.
Тесты 6–9. $P \le 10^7$, оцениваются в 30 баллов.
Тесты 10–12. Дополнительных ограничений нет, оцениваются в 40 баллов.

Примеры

Входные данные

22 1 0

Выходные данные

Входные данные

19 0 1

Выходные данные

#3855

Ожерелье

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Московская область, Интернет этап, 2011, Задача B ]

Дано ожерелье, состоящее из n красных или черных бусин, нанизанных на нить. Ожерелье представляет собой замкнутую окружность. Разрежем ожерелье на 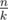$\text{[math]}$ связных цепочек по k бусин. Требуется написать программу, которая вычислит максимальное количество цепочек, состоящих только из красных бусин, которое можно получить среди всех способов разрезать ожерелье.

Входные данные

В первой строке входных данных содержатся два натуральных числа n и k, не превышающие 10⁶. Гарантируется, что k является делителем числа n. Во второй строке даны n чисел, разделенных одним проблеом, каждое из которых равно 0 или 1. i-ое число в этой последовательности обозначает цвет i-ой бусины в порядке обхода по часовой стрелке: 0 — черный, а 1 — красный, соответственно.

Выходные данные

В выходной файл выведите максимальное количество цепочек, состоящих из k красных бусин, которое возможно получить.

Примечание

Гарантируется, что решения, корректно работающие при ограничении N ≤ 10 000, будут оцениваться из 60 баллов.

Примеры

Входные данные

9 3
1 1 1 1 0 0 0 1 1

Выходные данные

Входные данные

9 3
0 1 1 1 1 0 1 1 1

Выходные данные