Дано прямоугольное шахматное поле размером n × m клеток (n столбцов, m строк), на котором находятся два короля. Для каждого короля даны его начальные координаты (x, y) и начальный вектор скорости (v_x, v_y). Числа v_x и v_y обозначают, что за один ход фигура передвигается на v_x клеток по горизонтали и на v_y по верткали, при этом числа v_x и v_y могут принимать значения  - 1, 0 и 1. Короли по очереди делают ходы в направлении своих векторов скоростей, меняя направления у стенок доски по закону отражения (при отражении от края доски одна из компонент скорости меняется, при отражении от угла меняются обе компоненты скорости). Если король после очередного хода попадает на клетку с королём противника, то он объявляется победителем и игра заканчивается. Первым ходит белый король.

Требуется определить, закончится ли игра и, в случае положительного ответа, кто из королей и на каком ходу выиграет.

Картина в голове Штирлица не складывалась. За год из Центра поступило N · M фрагментов нового задания. Штирлиц запомнил каждый фрагмент и теперь складывает из них целое сообщение.

Текст задания записан на клетчатой прямоугольной странице размера (5N)  ×  (5M), который разрезан на N · M частей. Каждый фрагмент сообщения можно представить квадратом 5  ×  5 (серые клетки), у которого с каждого краю (заштрихованные области) может быть только один «выступ» или «впадина». Обратите внимание, что к краям не относятся углы квадрата (см. иллюстрацию).

Более формально, каждый фрагмент можно представить в виде фигуры, которая получена из левой части иллюстрации, изменением цвета не более чем одной клетки из каждой заштрихованной области.

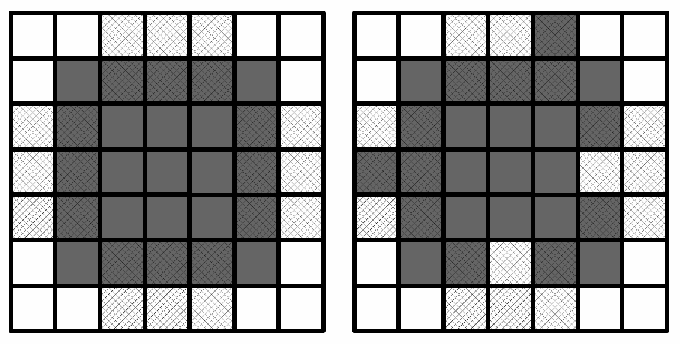
Фрагмент может иметь ровную сторону (т.е. не имеет выступа или впадины) только если соответствующая сторона фрагмента является границей сообщения.

Требуется написать программу, которая поможет Штирлицу собрать из фрагментов целое сообщение.

Всем известно, что в 2012 году прошла Летняя Олимпиада в Лондоне, однако не каждый знаком с историей крупнейших спортивных соревнований. Традиция игр зародилась в Древней Греции, но была забыта по завершении античной эпохи и вновь появилась лишь в конце XIX века благодаря французскому общественному деятелю Пьеру де Кубертену.

С 1896 года вновь проводятся летние Олимпийские игры, а с 1924 — зимние, причём оба вида соревнований проходят раз в четыре года. Первое время зимняя и летняя Олимпиады проводились в один и тот же год, но в конце XX века Международный олимпийский комитет принял решение установить между разными видами Игр двухгодичный перерыв. Таким образом, 1992 год был в последний раз отмечен проведением одновременно летних и зимних Олимпийских игр, в 1994 проводились только зимние, в 1996 — летние, и с тех пор они продолжают чередоваться.

Известно также, что в 1916, 1940 и 1944 годах Олимпийские игры были отменены по причине Первой и Второй мировых войн, а в 1906 году проводилась внеочередная Олимпиада.

Требуется написать программу, которая по заданному году определит, проводились ли в этом году Олимпийские игры и были ли они летними или зимними.

Мальчик Вася очень любит строить башни из кубиков. К сожалению, во время последней игры он увлёкся и потерял все кубики, кроме двух. Однако Вася не стал унывать и придумал новое развлечение. Заметив, что на каждой грани кубиков написано по одной цифре, он научился выкладывать двузначные числа из оставшихся игрушек. Вскоре мальчику стало интересно, сколько идущих подряд чисел, начиная с единицы, он сможет выложить с помощью двух кубиков. Помогите Васе найти ответ — такое максимальное число K, что все числа от 1 до K включительно можно получить, используя два оставшихся кубика.

Поскольку в игре используются оба кубика, числа, меньшие 10, Вася выкладывает с ведущими нулями (так, единицу можно получить, выбрав грань первого кубика с цифрой 0 и второго — с цифрой 1). Помните, что Вася умный мальчик: он знает, что перевернутый кубик с цифрой 6 позволяет получить цифру 9, и наоборот.

Дано натуральное число N. Требуется написать программу, которая находит такое минимальное число M, произведение цифр которого равно N.