Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
Сегодня утром жюри решило добавить в вариант олимпиады еще одну, Очень Легкую Задачу. Ответственный секретарь Оргкомитета напечатал ее условие в одном экземпляре, и теперь ему нужно до начала олимпиады успеть сделать еще N копий. В его распоряжении имеются два ксерокса, один из которых копирует лист за х секунд, а другой – за y. (Разрешается использовать как один ксерокс, так и оба одновременно. Можно копировать не только с оригинала, но и с копии.) Помогите ему выяснить, какое минимальное время для этого потребуется.
На вход программы поступают три натуральных числа N, x и y, разделенные пробелом (1 ≤ N ≤ 2∙108, 1 ≤ x, y ≤ 10).
Выведите одно число – минимальное время в секундах, необходимое для получения N копий.
4 1 1
3
5 1 2
4
Слово называется палиндромом, если его первая буква совпадает с последней, вторая – с предпоследней и т.д. Например: "abba", "madam", "x".
Для заданного числа K слово называется почти палиндромом, если в нем можно изменить не более K любых букв так, чтобы получился палиндром. Например, при K = 2 слова "reactor", "kolobok", "madam" являются почти палиндромами (подчеркнуты буквы, заменой которых можно получить палиндром).
Подсловом данного слова являются все слова, получающиеся путем вычеркивания из данного нескольких (возможно, одной или нуля) первых букв и нескольких последних. Например, подсловами слова "cat" являются слова "c", "a", "t", "ca", "at" и само слово "cat" (а "ct" подсловом слова "cat" не является).
Требуется для данного числа K определить, сколько подслов данного слова S являются почти палиндромами.
В первой строке вводятся два натуральных числа:N (1 ≤ N ≤ 5 000) – длина слова и K (0 ≤ K ≤ N).
Во второй строке содержится слово S, состоящее из N строчных латинских букв.
Требуется вывести одно число – количество подслов слова S, являющихся почти палиндромами (для данного K).
5 1 abcde
12
3 3 aaa
6
Новый учитель математики ввел в школе оригинальную систему оценки учеников – рейтинговую. На каждом уроке школьнику предлагалось выполнить задание, состоящее из нескольких задач. После этого учитель увеличивал рейтинг школьника на число, равное отношению количества решенных им сегодня задач к количеству задач, решенных им на прошлом занятии. Например, если сегодня ученик решил 5 задач, а вчера – две, то к его рейтингу сегодня прибавится = 2.5. Изначально рейтинг равен нулю; он начинает увеличиваться со второго дня. Если в один из дней какой-то ученик не решал ни одной задачи, то учитель объявлял его полной бездарностью и переводил в другой класс (с облегченным изучением математики), поэтому каждый день все ученики старались решить хотя бы одну задачу.
Школьники быстро обнаружили, что для получения наибольшего рейтинга им далеко не всегда нужно решать все задачи. Им известно, сколько задач учитель будет давать в каждый из дней. Помогите им определить, в какой день сколько задач следует решить, чтобы в итоге получить наибольший рейтинг.
В первой строке вводится одно натуральное число N (1 ≤ N ≤ 1 000) – количество уроков, которые провел в школе учитель до того, как его уволили.
В следующей строке содержатся числа a1,a2, …, aN– количество задач, которые учитель предложил школьникам на первом, втором, …, N-м уроках соответственно (1 ≤ ai ≤ 100).
В первой строке выведите максимальный рейтинг, который может получить школьник за N дней, с точностью не менее 0.001.
Во второй строке выведите N чисел – количество задач, которые должен решить школьник в каждый из дней. Если вариантов несколько, выведите один любой из них.
3 1 2 3
4.00000 1 1 3
3 1 10 8
10.800000 1 10 8
В ежегодном чемпионате Флатландии (которая, естественно, является плоским миром) по космическим гонкам "Формула-3" участвуют N космических скутеров, имеющие форму треугольников. До начала гонок скутеры занимают положение в стартовой зоне согласно результатам жеребьевки.
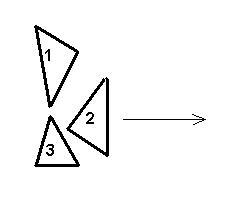
Скутеры стартуют строго по порядку. Каждый скутер,получив команду «старт», уезжает в положительном направлении оси Ox. Следующий скутер стартует лишь тогда, когда предыдущий покинет стартовую зону. Скутеры уезжают строго параллельно оси Ox, скутеры в стартовой зоне не поворачивают и не разворачиваются.
Естественно, что если в момент старта на пути скутера окажется другой скутер, то произойдет авария (даже если скутер заденет лишь угол другого скутера своим углом).
Для уменьшения опасности столкновения скутеров на старте строго соблюдается следующее правило: прямые, параллельные оси Ox и пересекающие какой-то скутер, должны в совокупности пересекать не более 100 других скутеров (прямая, проходящая через одну точку скутера также считается прямой, пересекающей скутер). Например, на приведенном рисунке прямые, параллельные Ox и пересекающие скутер 2, проходят через 2 других скутера (1 и 3), а прямые, проходящие через скутер 1, проходят только через один другой скутер (номер 2).
Главный Судья гонок хочет определить порядок, в котором должны стартовать скутеры, чтобы аварии не произошло. Например, в ситуации, приведенной на рисунке, сначала должен стартовать скутер номер 2 (если попытается стартовать скутер номер 1 или 3, то он столкнется со скутером номер 2). После этого скутеры 1 и 3 могут стартовать в любом порядке (они друг другу не мешают).
Помогите Главному Судье — напишите программу, которая определит какой-нибудь порядок старта скутеров, чтобы аварии не произошло.
В первой строке вводится натуральное число
В каждой из следующих N строк содержится по 6 чисел: x1, y1, x2, y2, x3, y3 – координаты трех вершин скутера на старте, целые числа, не превосходящие по модулю 106. В начальный момент скутеры не задевают друг друга.
Выведите через пробел N чисел – номера скутеров в том порядке, в котором они могут стартовать. Если решений несколько, выведите одно любое из них. Если решений нет, выведите одно число -1.
Примечание: первый тест соответствует приведенному рисунку. Ответ 2 3 1 в этом тесте также является правильным
3 1 19 3 9 6 15 5 6 10 2 10 12 1 1 6 1 3 7
3 0 1 -2 1 -1 -1 5 6 10 2 10 12 1 1 6 1 3 7
Поле для детской игры представляет собой последовательность кружков, первый из которых является стартом, а последний – финишем. На некоторых из кружков указано действие, которое нужно совершить фишке, попавшей на этот кружок: передвинуть фишку на несколько кружков вперед или назад, или сделать еще один ход. Изначально фишки всехK игроков ставятся на старт. Затем они по очереди делают ходы, которые заключаются в следующем. Игрок получает очередное "случайное" число, используя генератор псевдослучайных чисел, описанный ниже, и передвигает свою фишку на столько кружков вперед, какое число он получил (если это число больше количества кружков до финиша, то игрок останавливается на финише). Если на кружке, куда он попал в результате своего хода, написано, что требуется совершить некоторое действие, то игрок совершает это действие. После этого он совершает действие, указанное на кружке, куда он попал в результате предыдущего действия и т. д. до тех пор, пока он не попадет на кружок, на котором не указано никакого действия.
Игра заканчивается, как только фишка одного из игроков достигнет финиша. Этот игрок и считается победителем. Требуется написать программу, которая по описанию поля и по данным параметрам генератора псевдослучайных чисел определит, кто выиграет в данной игре.
Генератор псевдослучайных чисел устроен следующим образом. Его параметрами являются натуральные числа a, b, c и x0. Генератор порождает последовательность натуральных чисел x1, x2, x3, … по следующему правилу: xn+1 равно остатку от деления (axn+ b) на c (при n = 0, 1, 2, …). Для игры используются числа x1, x2, x3, … именно в этом порядке (число x0 не используется). Все игроки используют общий датчик, то есть, если, например, первый игрок использовал число x1 и передал ход второму, то тот будет использовать число x2, а если ему потребуется повторить ход, то x3 и т. д.
В первой строке входных данных содержатся числа a, b, c, x0, описывающие генератор псевдослучайных чисел. Все числа целые неотрицательные и не превосходят 1000; c > 0. В следующей строке записаны числа K – количество игроков и L – количество кружков поля, включая старт и финиш (1 ≤ K, L ≤ 1000). В следующих L–2 строках записаны команды во втором, третьем, …, L–1-м кружке (в кружках старта и финиша никаких команд нет и при попадании туда ничего делать не нужно). Каждая команда записывается парой чисел.
Если первое число равно единице, то это означает, что нужно сделать дополнительный ход. При этом, если второе число равно T и T > 0, то нужно сделать ход на T кружков вперед, если T < 0 – то на |T| кружков назад, а если T = 0, то нужно снова воспользоваться датчиком псевдослучайных чисел и сделать указанное им количество шагов вперед.
Если первое число равно нулю, то ничего делать не нужно. (Если первое число равно нулю, то второе число также равно нулю.)
Другие значения первое число принимать не может.
Число T целое, и всегда таково, что при соответствующем ходе фишка не окажется за пределами доски (но может оказаться на клетке Старт или Финиш). Если же T = 0 и очередное "случайное" число больше, чем количество кружков до финиша, то фишка останавливается на финише.
Выведите одно число – номер игрока-победителя. Гарантируется, что одна из фишек обязательно достигнет финиша, причем за время игры будет совершено не более миллиона перемещений (на "случайное" число или число, указанное в кружке).
1 1 100 1 2 5 0 0 0 0 1 1
2 3
1 1 100 1 2 5 0 0 1 0 1 1
1 2