Сегодня день рождения Никиты. На празднование дня рождения приглашены n детей (включая самого Никиту). Все дети пронумерованы числами от 1 до \(n\). Работники МакДональдса приготовили большой круглый стол и поставили вокруг него n стульев.
Как только дети приходят на день рождения, они рассаживаются за столом. Ребенок с номером 1 занимает одно из мест. Ребенок с номером 2 занимает место слева от ребенка с номером 1. Ребенок с номером 3 занимает следующее за ним место слева и так далее. Наконец, ребенок с номером \(n\) займет оставшееся свободное место между детьми с номерами \(n\) – 1 и 1.
Работники МакДональдса хорошо знают, что некоторые из приглашенных детей ведут себя весьма шумно за столом, если сидят друг с другом. Поэтому работники ресторана собираются пересадить детей в некотором порядке. Этот порядок описывается перестановкой \(p_1\), \(p_2\),..., \(p_n\) (\(p_1\), \(p_2\),..., \(p_n\) — различные целые числа от 1 до \(n\)). То есть, ребенок \(p_1\) должен сидеть между \(p_n\) и \(p_2\), ребенок \(p_i\) (i = 2, 3, ... , \(n\) − 1) должен сидеть между \(p\)i-1 и \(p\)i+1; ребенок \(p_n\) должен сидеть между \(p\)n-1 и \(p_1\).
К сожалению, все дети пришли и расселись так, как указано в первом абзаце. Поэтому для того, чтобы рассадить детей в нужном порядке, придется пересадить кого-то из детей на некоторое количество мест влево или вправо. Для каждого ребенка работникам ресторана необходимо решить, как он будет пересаживаться: они должны выбрать направление (влево или вправо) и расстояние (на сколько мест нужно переместиться). Затем, по заданному сигналу все дети должны одновременно встать и переместиться на места, определенные работниками МакДональдса.
Пересаживание детей вносит беспорядок в празднование дня рождения. Величина беспорядка пропорциональна максимальному из расстояний, на которые дети будут пересажены. Пересаживание детей можно организовать многими способами. Работники МакДональдса решили выбрать тот из них, при котором величина беспорядка будет минимальной, то есть тот способ, при котором максимальное из расстояний пересаживания будет минимальным. Помогите им найти такой способ.
Имейте в виду, что ребенок \(p_i\) может сидеть как слева, так и справа от ребенка \(p_n\).
Ваша задача — написать программу, которая:
· читает из стандартного ввода количество детей и перестановку, определяющую желаемый порядок рассадки детей,
· вычисляет минимально возможную величину беспорядка,
· выводит результат в стандартный вывод.
В первой строке стандартного ввода содержится единственное целое число \(n\) (1 \(\le\) n \(\le\) 1 000 000). Во второй строке содержатся \(n\) целых чисел \(p_1\), \(p_2\),..., \(p_n\), разделенных одним пробелом. Числа \(p_1\), \(p_2\),..., \(p_n\) образуют перестановку множества {1, 2, ... , \(n\)}, описывающую желаемый порядок рассадки детей. Кроме того, в 50% тестов число \(n\) не будет превышать 1 000.
В первую и единственную строку стандартного вывода выведите единственное число — минимально возможное из максимальных расстояний, на которые придется пересесть детям.
На рисунке слева изображена исходная рассадка детей. На рисунке в середине показан результат пересаживания, при котором дети с номерами 1 и 2 перемещаются на одно место, дети с номерами 3 и 5 перемещаются на два места и дети с номерами 4 и 6 не меняют своего положения. Требуемые условия рассадки выполнены, поскольку 3-й сидит между 6-м и 4-м, 4-й сидит между 3-м и 5-м, 5-й сидит между 4-м и 1-м, 1-й сидит между 5-м и 2-м, 2-й сидит между 1-м и 6-м и 6-й сидит между 2-м и 3-м. Также существует другой вариант конечной рассадки детей, изображенный на рисунке справа. В обоих вариантах величина беспорядка равна 2.
6 3 4 5 1 2 6
2
Ограничение памяти: 32 MB
Ограничение времени: 14 сек
Вы можете предполагать, что суммарное время работы библиотеки в процессе тестирования не будет превышать 4 сек.
Загрузить библиотеку для тестирования
Рассмотрим игру для двух игроков. Игрокам дан прямоугольник размером x × y (где x и y — положительные целые числа). Игроки ходят по очереди. Ход состоит в разделении прямоугольника на два прямоугольника одним горизонтальным или вертикальным разрезом. Полученные прямоугольники должны иметь положительные целочисленные размеры.
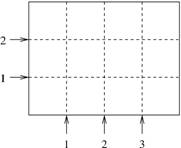
Возможные разрезы прямоугольника размером 4 × 3.
После каждого разреза прямоугольник с меньшей площадью убирается, а оставшийся передается другому игроку. Если прямоугольник разделен на две равные части, то убирается одна из них. Игрок, который получает прямоугольник размером 1 × 1, проигрывает, так как не может сделать следующий ход.
Ваша задача — написать программу, которая бы играла в игру с прямоугольниками и выигрывала. Для того чтобы играть, программа должна использовать специальную библиотеку. В библиотеке есть функции dimension_x() и dimension_y(), возвращающие размеры прямоугольника. Начальные размеры прямоугольника — целые числа от 1 до 100 000 000. Как минимум один из размеров больше 1. К тому же, в 50% тестов размеры прямоугольника не будут превышать 25.
В библиотеке есть также процедура cut(dir, position), которая должна вызываться вашей программой, чтобы сделать ход. Параметры dir и position описывают направление и позицию разреза соответственно. Параметр dir может принимать одно из двух значений: vertical и horizontal. Если dir = vertical, то проводится вертикальный разрез, а параметр position указывает x - координату разреза, как показано на рисунке выше. При этом вы должны гарантировать выполнение неравенства 1 ≤ position ≤ dimension_x()− 1. Если dir = horizontal, то проводится горизонтальный разрез, а параметр position указывает y ‑ координату разреза. При этом, вы должны гарантировать выполнение неравенства 1 ≤ position ≤ dimension_y()− 1.
После запуска вашей программы она будет играть за одного из игроков. Ваша программа ходит первой, она должна разрезать исходный прямоугольник. Когда ваша программа вызывает процедуру cut, ваш ход записывается и управление передается программе соперника. После хода соперника управление возвращается вашей программе. Значения, которые возвращаются функциями dimension_x() и dimension_y(), будут отражать результат вашего хода и хода соперника. Как только ваша программа выигрывает, проигрывает или делает неправильный ход, ее исполнение будет прервано. Прерывание вашей программы — это автоматический процесс, так что ваша программа должна продолжать делать столько ходов, сколько возможно до автоматического прерывания ее исполнения. Вы можете предполагать, что для предложенных входных данных всегда существует выигрышная стратегия для вашей программы.
Ваша программа не должна читать какие-либо файлы или писать в них, не должна использовать стандартный ввод и вывод и не должна пытаться изменять содержимое какой-либо памяти вне вашей программы. Нарушение любого из этих правил может привести к дисквалификации.
Экспериментирование
Для того, чтобы дать вам возможность поэкспериментировать с библиотекой, в ваше распоряжение предоставлены примеры библиотек: их исходные тексты находятся в файлах preclib.pas, creclib.c и creclib.h . Эти библиотеки вы можете взять по адресу: http :// contest / . Они реализуют очень простую стратегию. Когда вы запустите вашу программу, она будет играть против этих простых соперников. Вы можете изменять их, чтобы протестировать вашу программу с лучшими соперниками. Следует учесть, что во время тестирования после окончания тура, ваша программа будет играть против другого соперника.
При посылке вашей программы на проверку с использованием интерфейса TEST , она будет откомпилирована с немодифицированной библиотекой соперника. При этом посылаемый вами входной файл будет передан как стандартный ввод вашей программе. Входной файл должен состоять из двух строк, каждая из которых должна содержать по одному целому числу. Первая строка должна содержать исходную ширину, вторая — исходную высоту прямоугольника. Эти размеры будут прочитаны библиотекой, предложенной в качестве примера.
Если вы модифицируете часть implementation библиотеки preclib.pas, пожалуйста, перекомпилируйте её, используя команду ppc386 -O2 preclib.pas. Эта команда создаст файлы preclib.o и preclib.ppu. Эти файлы необходимы для компиляции вашей программы и должны быть в помещены в каталог, где находится ваша программа. Пожалуйста, не модифицируйте часть interface библиотеки preclib.pas.
Если вы модифицируете библиотеку creclib.c, пожалуйста, не забудьте поместить ее вместе с creclib.h в каталог, где находится ваша программа, — они необходимы для компиляции. Пожалуйста, не модифицируйте файл creclib.h.
В ваше распоряжение также предоставляются две простые программы, которые иллюстрируют использование библиотек crec.c и prec.pas. Пожалуйста, помните, что эти программы не являются правильными решениями. Вы можете откомпилировать их, используя такие команды:
gcc -O2 -static crec.c creclib.c -lm
g++ -O2 -static crec.c creclib.c -lm
ppc386 -O2 -XS prec.pas
Библиотеки
В ваше распоряжение предоставлены библиотеки, которые обеспечивают следующую функциональность:
- Библиотека для FreePascal (preclib.ppu, preclib.o)
type direction = (vertical, horizontal);
function dimension_x(): longint;
function dimension_y(): longint;
procedure cut(dir: direction; position: longint);
Включите следующий оператор в ваш исходный файл rec.pas:
uses preclib;
Чтобы откомпилировать вашу программу, скопируйте файлы preclib.o и reclib.ppu в каталог, где находится ваш исходный файл, и выполните следующую команду:
ppc386
-O2 -XS rec.pas
Файл prec.pas является примером использования библиотеки preclib.
- Библиотека для GNU C/C++ (creclib.h, creclib.c)
typedef enum __direction {vertical, horizontal} direction;
int dimension_x();
int dimension_y();
void cut(direction dir, int position);
#include ”creclib.h”
Чтобы откомпилировать вашу программу, скопируйте файлы creclib.c и creclib.h в каталог, где находится ваш исходный файл, и выполните следующую команду:
gcc -O2 -static rec.c creclib.c –lm
или:
g++ -O2 -static rec.cpp creclib.c –lm
Файл crec.c является примером использования библиотеки в C.
Пример взаимодействия
Ниже приведен пример взаимодействия вашей программы с библиотекой. Он показывает, как может проходить игра. Игра начинается с прямоугольника размером 4 × 3. Существует выигрышная стратегия для этого случая.
|
Ваша программа вызывает |
Что происходит |
|
dimension_x() |
возвращает 4 |
|
dimension_y() |
возвращает 3 |
|
cut(vertical, 1) |
ваш разрез записывается, и прямоугольник размером 3 × 3 передается вашему сопернику, который разрезает его и получается прямоугольник размером 3 × 2; после этого управление передается вашей программе |
|
dimension_x() |
возвращает 3 |
|
dimension_y() |
возвращает 2 |
|
cut(horizontal, 1) |
ваш разрез записывается, и прямоугольник размером 3 × 1 передается вашему сопернику, который разрезает его и получается прямоугольник размером 2 × 1; после этого управление передается вашей программе |
|
dimension_x() |
возвращает 2 |
|
dimension_y() |
возвращает 1 |
|
cut(vertical, 1) |
в результате вашего разреза получается прямоугольник размером 1 × 1, так что вы выиграли; после этого работа вашей программы автоматически прекращается. |
Почти все Королевство Байтленд покрыто лесами и реками. Малые реки сливаются в более крупные реки, которые, в свою очередь, сливаются друг с другом; в конечном счете, все реки сливаются вместе в одну большую реку. Большая река впадает в море вблизи города Байттаун.
В Байтленде имеется n лесозаготовительных поселков, каждый из которых расположен вблизи какой-либо реки. В настоящее время в Байттауне находится большая пилорама, которая обрабатывает все деревья, срубленные в Королевстве. Деревья сплавляются вниз по рекам от поселков, где они срублены, к пилораме в Байттауне. Король Байтленда решил поставить k дополнительных пилорам в поселках, чтобы уменьшить стоимость сплава деревьев. После установки пилорам деревья не обязательно должны сплавляться в Байттаун, а могут быть обработаны на ближайшей пилораме, находящейся ниже по течению рек. Очевидно, что деревья, срубленные в окрестности поселка с пилорамой, вообще не сплавляются по рекам.
Необходимо отметить, что реки в Байтленде не разветвляются. Из этого следует, что для каждого поселка существует единственный путь сплава деревьев вниз по течению рек от него в Байттаун.
Королевские счетоводы подсчитали количество деревьев, срубаемых в каждом поселке за год. Вам необходимо определить, в каких поселках следует установить пилорамы, чтобы минимизировать общую стоимость сплава деревьев за год. Стоимость сплава одного дерева составляет один цент за каждый километр пути.
Напишите программу, которая:
<>
* читает из стандартного ввода количество поселков, количество дополнительных пилорам, которые будут установлены, количество срубленных в каждом поселке деревьев и описание рек,
*вычисляет минимальную стоимость сплава деревьев после установки дополнительных пилорам,
*выводит результат в стандартный вывод.
Первая строка входных данных содержит два целых числа: \(n\) — количество поселков, не считая Байттауна (2 ≤ \(n\) ≤ 100), и \(k\) — количество дополнительных пилорам, которые будут установлены (1 ≤ \(k\) ≤ 50 и \(k\) ≤ \(n\) ). Поселки нумеруются числами 1 , 2 , ...., n , а Байттаун имеет номер 0.
Каждая из последующих n строк содержит три целых числа, разделенных одним пробелом. Строка i + 1 содержит:
\(w_i\) — количество деревьев, срубаемых в поселке \(i\) за год (0 ≤ \(w_i\) ≤ 10 000),
\(v_i\) — ближайший поселок (либо Байттаун) вниз по реке от поселка \(i\) (0 ≤ \(v_i\) ≤ \(n\) ),
\(d_i\) — расстояние (в километрах) по реке от поселка \(i\) до поселка \(v_i\) (1 ≤ \(d_i\) ≤ 10 000).
Гарантируется, что суммарная стоимость сплава всех деревьев к пилораме в Байттауне не превосходит 2 000 000 000 центов в год.
В 50% тестов число n не превосходит 20.
Первая и единственная строка выходных данных должна содержать одно целое число: минимальную стоимость сплава (в центах).
Рисунок сверху иллюстрирует входные данные примера. Номера поселков указаны внутри кругов. Числа под кругами обозначают количество деревьев, срубаемых вблизи данного поселка. Числа над стрелками указывают длины рек.
Пилорамы должны быть установлены в поселках 2 и 3.
4 2 1 0 1 1 1 10 10 2 5 1 2 3
4