Темы
Информатика(2656 задач)
--->
61 задач
<---
#1358
Темы:
[Перебор]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
На заводе каждая из N деталей может быть обработанной на одном из двух станков: A или B. Каждая деталь имеет порядковый номер от 1 до N. К обработке детали поступают последовательно, в соответствии со своими номерами. Количество деталей всегда четно.
Существуют правила, по которым определяется можно ли обрабатывать деталь на определенном станке.
- Если на текущий момент на станке B было обработано такое же количество деталей, как и на станке A, то следующая деталь должна быть обработана на станке A.
- В итоге на каждом из станков должно быть обработано одинаковое количество деталей.
Сколько людей, столько и мнений. Каждый из работников этого завода предложил свою последовательность обработки деталей, причем все предложения оказались разными, но удовлетворяющими правилам 1 и 2.
Напишите программу, которая по информации о количестве деталей N определяет максимально возможное количество работников завода.
Входные данные
Единственная строка входного файла содержит четное число N (2≤N≤28) – количество деталей которое необходимо обработать.
Выходные данные
Единственная строка выходного файла должна содержать целое число – максимально возможное количество работников завода.
Первый работник считает, что на станке A необходимо обработать детали 1 и 2, а на станке B, соответственно, 3 и 4. Второй думает, что на станке A нужно обработать детали 1 и 3, а на станке B – детали 2 и 4. Других вариантов последовательности обработки не существует.
Примеры
Входные данные
4
Выходные данные
2
#1359
Темы:
[Жадный алгоритм]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Робот движется по полю, которое состоит из N клеток, выстроенных в ряд. На каждой из клеток находится кубик определенного цвета.
До начала движения робот находится на первой клетке поля и не держит ни одного кубика. Находясь на клетке, робот может выполнить не более одного раза каждую из следующих операций: (1) положить кубик того же цвета, который лежит на текущей клетке; (2) поднять с клетки тот кубик, который находился там сначала. После этого робот перемещается на следующую клетку или останавливается, если текущая клетка последняя в поле.
Одновременно робот может держать не более K кубиков. На момент остановки робот не должен держать ни одного кубика.
Напишите программу, которая по информации о цвете кубиков и ограничении на количество кубиков, которое может держать робот, определяет максимальное общее количество кубиков, которое робот может перенести с места на место, двигаясь по полю.
Входные данные
Первая строка входного файла содержит символьную строку длинны N (1≤N≤1000). Строка состоит из маленьких букв латинского алфавита. Каждая буква соответствует клетке поля и определяет цвет кубика, который находится в этой клетке. Вторая строка содержит ограничение на количество кубиков, которое одновременно может держать робот K (1≤K≤25).
Выходные данные
Единственная строка выходного файла должна содержать целое число — максимальное количество кубиков, месторасположение которых робот может изменить, двигаясь по полю.
Подзадачи и система оценки
Баллы за эту задачу будут начислены если ваше решение проходит все тесты
Примеры
Входные данные
rgbbggrmcm 2
Выходные данные
4
#1360
Темы:
[Вычислительная геометрия]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
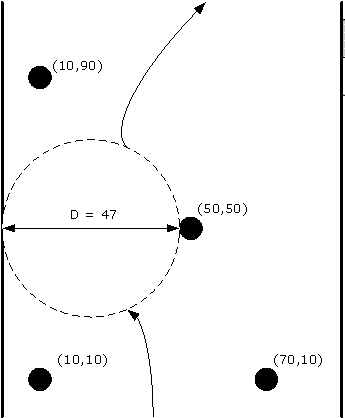Единственный способ попасть в Зал Круглых Столов – пройти через Колонный Коридор. Стены Коридора изображаются на карте прямыми линиями, которые параллельны оси OY системы координат. Вход в Коридор находится снизу, а выход из Коридора в Зал – сверху. В Коридоре есть цилиндрические (на карте круглые) Колонны одинакового радиуса R.
Напишите программу, которая по информации о размерах Коридора, и размещения Колонн определяет диаметр наибольшего из Круглых Столов, который можно пронести через такой Коридор, сохраняя поверхность Стола горизонтальной.
Входные данные
В первой строке входного файла заданы два числа XL и XR – x-координаты левой и правой стен Коридора. Во второй строке находится целое число R (1≤R≤1 000 000) – радиус всех Колонн. В третей – целое число N (1≤N≤200), которое задает количество Колонн. Далее следуют N строк, в каждой из которых по два числа – x- и y-координаты центра соответствующей Колонны.
Все входные координаты – целые числа, которые по модулю не превосходят 1 000 000.
Выходные данные
Единственная строка выходного файла должна содержать одно число – искомый диаметр наибольшего Стола. Диаметр следует выводить с точностью 3 знака после десятичной точки (даже в случае, когда он окажется целым). Если нельзя пронести ни одного Стола, то ответ должен быть: 0.000
Точность 3 знака после точки, по обычным правилам округления, обозначает, что ответ, который выдается в выходной файл, должен отличаться от точного не более чем на 510-4 (т.е. на 0.0005). Например, если точный ответ 1.234567, то в файле должно находится число 1.235. Если точный ответ 5.0005, то необходимо округлять в большую сторону, т.е. в файл следует выдать 5.001
Примеры
Входные данные
0 90 3 4 10 10 70 10 50 50 10 90
Выходные данные
47.000
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
В ток-шоу принимают участие N знакомых между собой людей, среди которых могут быть те, которые всегда говорят неправду, а остальные всегда говорят правду (по крайней мере один человек). В конце программы ведущий решил определить, кто из участников к какой из групп принадлежит. Для этого он задал вопрос: «Сколько среди вас тех, кто всегда говорит правду?». Каждый из участников дал ответ: число от 0 до N. После этого ведущий может отобрать определенных людей, задать им тот же самый вопрос, и, получив ответ, гарантированно определить, кто из участников ток-шоу говорит правду, а кто лжет. Участники отвечают на второй вопрос относительно выбранных ведущим людей.
Напишите программу, которая по количеству участников ток-шоу и их ответам на первый вопрос найдет минимальное количество людей, которое нужно выбрать ведущему для второго этапа опроса.
Входные данные
Первая строка входного файла содержит одно целое число N (1≤N≤1000) – количество участников ток-шоу. Следующая строка содержит N целых чисел от 0 до N – ответы каждого из участников на первый вопрос.
Выходные данные
Единственная строка выходного файла должна содержать целое число – искомое минимальное количество участников, которое необходимо выбрать ведущему для повторного опроса. В случае, если ведущий имеет возможность определить лжецов и тех, кто всегда говорит правду, уже после первого этапа опроса, нужно вывести число 0.
Примеры
Входные данные
4 3 1 3 3
Выходные данные
2
Входные данные
3 1 2 3
Выходные данные
0
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Клуб активного туризма на планете Олимпия решил предложить клиентам маршрут вдоль живописного хребта. Хребет достаточно длинный и его трудно пройти сразу, поэтому в клубе ищут самый привлекательный из маршрутов ограниченной длины. Согласно результатам социального исследования туристы любят проходить по местам, которые выше чем другие на как можно большем промежутке, благодаря более широкому обзору и эйфории от ощущения высоты.
Для упрощения задачи хребет разделили на однометровые отрезки и определили среднюю высоту над уровнем моря каждого из них. Численное значение привлекательности каждого такого отрезка хребта равно количеству последовательных отрезков слева и справа, начиная с непосредственных его соседей, которые имеют высоту строго меньшую чем он сам. Сам отрезок в эту сумму не входит. Привлекательность маршрута вычисляется как сумма привлекательностей однометровых отрезков хребта, которые в него входят. Длина маршрута должна быть не больше чем T метров. Направление маршрута значения не имеет, поскольку не меняет его привлекательности. Маршрут может начинаться с любого отрезка хребта. Маршрут не может содержать разрывов, то есть в маршрут можно включать только последовательные отрезки хребта.
Напишите программу, которая по информации о высоте над уровнем моря каждого однометрового отрезка горного хребта вычислит привлекательность наиболее привлекательного маршрута длины не больше чем T метров.
Входные данные
Первая строка входного файла содержит два целых числа N – длина всего хребта в метрах и T (1≤T≤N≤100 000) – ограничение на длину маршруту. Вторая строка файла содержит N целых чисел от 1 до 106 – высоты последовательных однометровых отрезков.
Выходные данные
Единственная строка выходного файла должна содержать одно целое число – численное значение привлекательности самого привлекательного маршрута вдоль горного хребта длины не более чем T.
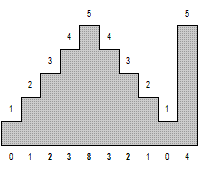
На рисунке изображен хребет, который соответствует входным данным, разбитый на 10 отрезков. Числа сверху соответствуют высоте каждого из отрезков, а числа снизу – привлекательности соответствующего отрезка.
Подзадачи и система оценки
Решения, работающие для случая \(NT < 4 \cdot 10^6\) будут оцениваться из 40 баллов
Примеры
Входные данные
10 5 1 2 3 4 5 4 3 2 1 5
Выходные данные
18
Выбрано
:
|