Пусть A — массив, состоящий из N элементов A1,...,AN. Обозначим его максимальное и минимальное значение как max(A) и min(A>) соответственно. Вычислим сумму элементов S, S=A1+A2+…+AN. Заменим каждый элемент массива на разницу S и этого элемента: Ai:=S-Ai, 1 ≤ i ≤N. Такое преобразование массива A назовем операцией Confuse.
Напишите программу, которая по массиву B, полученному в результате K–кратного применения операции Confuse к некоторому массиву A, вычислит разность max(A)-min(A).
Первая строка входного файла содержит целые числа N и K, где N — количество элементов массива B (2 ≤ N ≤ 10000), а K — количество применений операции Confuse к начальному массиву A, 1 ≤ K ≤ 100. Вторая строка файла содержит N элементов массиваB. Элементы массива B — целые числа, принадлежащие диапазону от -2 000 000 000 до 2 000 000 000.
Единственная строка выходного файла должна содержать целое число, которое есть разностью max(A) и min(A).
3 2 5 6 7
2
В спортивном турнире принимает участие N человек, с номерами от 1 до N. Турнир проходит по круговой системе: каждый участник должен сыграть с каждым другим участником по одной партии, которая заканчивается победой одного из игроков. Считается, что по окончании турнира участник занимает место P, если:
- у него выиграли (P-1) участников, и ему проиграли все остальные;
- все участники, которые победили его, выиграли свои партии у всех участников, которые ему проиграли.
Для остальных участников итоговое место определить нельзя.
Напишите программу , которая получает на вход число N и результаты сыгранных на данный момент партий турнира, и определяет количество участников, для которых по окончании турнира нельзя будет определить итоговое место, в независимости от результатов тех партий, которые еще будут сыграны.
В первой строке задаются два натуральных числа: N — количество участников турнира (1N100) и M — количество сыгранных партий. Следующие M строк описывают сыгранные партии. В строке задается два числа: номер победителя и номер проигравшего.
В единственной строке выходного файла должно быть целое число — искомое количество участников.
6 6 3 4 4 5 1 2 4 1 1 6 5 3
3
| a | a | b | r | a | k |
| a | b | r | a | k | a |
| a | k | a | a | b | r |
| b | r | a | k | a | a |
| k | a | a | b | r | a |
| r | a | k | a | a | b |
Во время своей работы алгоритм сжатия данных методом «сортировки блока» применяет к блокам данных преобразование, которое определяется следующим образом.
Строка P называется ротацией строки S, если она образована циклическим сдвигом символов S, т.е. если S=a1a2…aN, где ai — i–ый символ строки S, то P=apap+1…aNa1…ap-1, где 1pN. Рассмотрим таблицу M размера NN, строками которой есть все ротации строки S, отсортированные в лексикографическом (словарном) порядке
по возрастанию.
Пусть строка L есть последний столбик таблицы M. Прямое преобразование получает на вход строку S, выдает строку L и число K — номер строки таблицы M, который содержит строку S. (Если таких строк несколько, выдается номер любой из них).
Для S='abraka' таблица M изображена на рисунке. Строка S находится во второй строке таблицы M, L=‘karaab’.
Напишите программу, которая выполняет обратное преобразование, т.е. получает на вход строку L и число K, и выдает строку S.
Первая строка входного файла содержит два целых числа: K и N, 1 ≤ N ≤30000, 1&let;K≤N. Вторая строка содержит N символов строки L — маленьких латинских букв.
Единственная строка выходного файла должна содержать строку S.
2 3 unn
nun
3 7 jubcirt
irtucjb
На циферблате записана последовательность чисел в двоичной системе счисления. Линии разбиения могут проходить как между числами, так и между цифрами одного числа, разбивая его на два или больше чисел. Для каждого сектора можно посчитать сумму чисел, которые в нем расположены.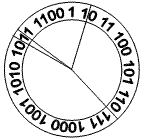 
Каждое число в последовательности не равно 0, и его запись начинается с единицы. Количество цифр в двоичной записи числа не превышает 25. Общее количество цифр на циферблате не больше чем 100.
Циферблат может быть разбит на сектора. На рисунке изображен привычный нам циферблат с числами от 1 до 12 (в немного непривычном виде). Он разбит на 4 сектора. Суммы в секторах будут 1, 15, 18 и 36.
Напишите программу, которая по заданной последовательности определяет количество разных разбиений циферблата на сектора, таких что сумма чисел во всех секторах одинакова.
В единственной строке входного файла задана последовательность чисел. Числа последовательности разделены пробелом.
В единственной строке выходного файла должно находиться натуральное число — количество искомых разбиений циферблата на сектора.
10 11 10
9
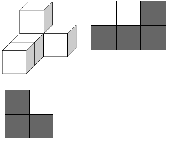Трехмерная фигура состоит из единичных кубиков. По фигуре можно построить ее фронтальную и правую проекции. Очевидно, что по этим двум проекциям не всегда можно восстановить фигуру.
Напишите программу, которая получает на вход фронтальную и правую проекции фигуры и определяет минимальное и максимальное количество кубиков, которое можно было бы использовать для построения фигуры с заданными проекциями.
В первой строке входного файла находятся три числа N, M и К, которые задают размеры проекций (1≤N, M, K≤100). Дальше задаются две проекции: сначала фронтальная, а затем правая. Проекция задается N строками, каждая из которых состоит из чисел 0 и 1, разделенных пробелами. Для фронтальной проекции таких чисел будет M, а для правой — K. 0 означает свободную клетку проекции, 1 — заполненную.
В единственной строке выходного файла должно находиться два числа: минимальное и максимальное число кубиков, которые можно было бы использовать для построения фигуры с заданными проекциями.
2 2 3 1 0 1 1 0 0 1 1 1 1
4 7