С целью подготовки к проведению олимпиады по информатике мэр решил обеспечить надежным электроснабжением все школы города. Для этого необходимо провести линию электропередач от альтернативного источника электроэнергии “Майбуття” к одной из школ города (к какой неважно), а также соединить линиямии электропередач некоторые школы между собой.
Считается, что школа имеет надежное электроснабжение, если она напрямую связана с источником “Майбуття”, либо с одной из тех школ, которые имеют надежное электроснабжение.
Известна стоимость соединения между некоторыми парами школ. Мэр города решил выбрать одну из двух наиболее экономичных схем электроснабжения (стоимость схемы равняется сумме стоимостей соединений пар школ).
Напишите программу, которая вычисляет стоимость двух наиболее экономных схем альтернативного электроснабжения школ.
В первой строке входного файла находятся два натуральных числа, разделенных пробелом:N (3 ≤ N ≤ 100), количество школ в городе, и M – количество возможных соединений между ними. В каждой из последующих M строк находятся по три числа: Ai, Bi, Ci, разделенных пробелами, где Ci – стоимость прокладки линии электроснабжения (1 ≤ Ci ≤ 300) от школы Ai до школы Bi (i=1,2,…,N).
В единственной строке выходного файла должны содержаться два натуральных числа S1 и S2, разделенных пробелом – две наименьшие стоимости схем (S1 ≤ S2). S1=S2 тогда и только тогда, когда существует несколько схем надежного электроснабжения наименьшей стоимости.
Гарантируется, что для входных данных существует две различные схемы надёжного электроснабжения.
5 8 1 3 75 3 4 51 2 4 19 3 2 95 2 5 42 5 4 31 1 2 9 3 5 66
110 121
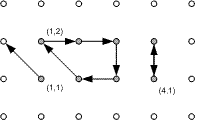На плоскости задано множество точек (x, y), где x, y – целые числа, 1≤x≤M, 1≤y≤N. Из каждой точки выходит ровно один из следующих векторов: (-1,-1), (-1,0), (-1,1), (0,1), (1,1), (1,0), (1,-1), (0,-1). Каждый вектор соединяет одну целочисленную точку плоскости с другой. Например, если из точке (2, 5) выходит вектор (1, 1), то он соединяет эту точку с (3, 6), но не наоборот.
Последовательность из двух и более точек плоскости a1, a2,…, ak назовем циклом, если каждая точка ai соединена вектором с ai+1 (1≤i≤k-1), и ak соединена вектором с a1. Циклы считаются разными если они отличаются хотя бы одной вершиной.
Напишите программу, которая по информации о векторах, выходящих из точек плоскости, находит количество различных циклов.
Первая строка входного файла содержит два целых числа N (1≤N≤100) и M (1≤M≤100). Каждая из последующих N строк, содержит M пар чисел (т.е. 2≤M чисел). Пара x, которая находится в строке y, задает вектор в точке (x, y).
Единственная строка выходного файла должна содержать целое число – количество циклов, образованных векторами.
2 4 -1 1 -1 1 -1 0 0 1 1 0 1 0 0 -1 0 -1
2
Набор домино состоит из прямоугольных костяшек, каждая из которых разделена на две половинки линией, параллельной более короткой стороне. На каждой из половинок нарисованы точки, количество которых соответствует числу от 0 до \(M\) включительно. На костяшках полного набора домино обозначены все возможные различные пары чисел, например, если M равно 3, то полный набор содержит 10 костяшек: (0, 0), (0, 1), (0, 2), (0, 3), (1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (3, 3).
Из костяшек можно выкладывать цепочки, соединяя пары костяшек короткими сторонами, если количества точек на соседних с местом соединения половинках костяшек равны.
Некоторые костяшки были удалены из полного набора. Требуется определить, какое минимальное количество цепочек нужно выложить из оставшихся в наборе костяшек, чтобы каждая из них принадлежала ровно одной цепочке.
Напишите программу, которая по информации о наборе домино должна ответить, какое минимальное количество цепочек нужно выложить.
В первой строке входного файла содержится одно целое число \(M\) (0≤\(M\)≤100), которое соответствует максимально возможному количеству точек на половинке костяшки. Во второй строке записано одно целое число \(N\), равное количеству костяшек, удаленных из полного набора. Каждая \(і\)-я из последующих \(N\) строк содержит по два числа \(A_i\) и \(B_і\). Это количества точек на половинках \(i\)-й удалённой костяшки.
Единственная строка выходного файла должна содержать одно целое число \(L\) – минимальное количество цепочек.
7 2 7 5 3 4
2
В стране Олимпия очень развита живопись. Картиной считается любой прямоугольник, который состоит из черных и белых единичных квадратов. Художник Олимпус решил радикально улучшить свои картины. Для этого он планирует к белому и черному цветам добавить еще и серый оттенок. По его задумке, граница между каждыми черным и белым квадратом должна содержать серую линию, чтобы образовался эффект плавного перехода.
Однако, перед началом работы, он обнаружил, что серая краска очень дорого стоит. Чтобы сэкономить деньги художник решил оценить, не выгоднее ли сначала перекрасить некоторые белые квадраты в черные, а черные в белые для того, чтобы минимизировать расходы на краску.
Напишите программу, которая по информации о существующей картине определяет минимальную сумму денег, которые понадобятся на ее улучшение.
Формат входных данных
Первая строка входного файла содержит пять натуральных чисел N, M, w, b, g. 1≤N, M≤70 – высота и ширина картины, 1≤w,b,g≤1000 – цена рисования одного белого единичного квадрата, черного единичного квадрата и серой линии единичной длины, соответственно. Далее следует N строк, каждая из которых состоит из M литер. Литера B соответствует черному квадрату, а W – белому.
Формат выходных данных
Единственная строка выходного файла должна содержать одно целое число, которое есть минимальной суммой затрат на улучшение картины.
3 2 10 12 1 BW WB BW
7