Заключительный этап 2010(4 задач)
Заключительный этап 2012(4 задач)
Заключительный этап 2013(5 задач)
Заключительный этап 2015(5 задач)
В тактике футбола одним из основных понятий является схема игры. Она определяет, сколько из десяти полевых игроков будут играть в защите, сколько — в полузащите и сколько — в нападении.
Например, схема игры 5-3-2 означает, что в команде пять защитников, три полузащитника и два нападающих. В соответствии с современными представлениями на схему игры накладываются следующие ограничения: должно быть не менее одного и не более пяти защитников, не менее одного и не более пяти полузащитников и не более трех нападающих. Отметим, что нападающих может в команде и не быть совсем. Будем рассматривать только такие схемы.
Будем считать, что футбольное поле имеет длину 120 метров и ширину 80 метров. Введем на нем прямоугольную декартову систему координат таким образом, как показано на рисунке. Ворота рассматриваемой нами команды находятся слева.
Будем также считать, что игрок в некоторый момент времени находится в линии полузащиты, если он находится на расстоянии не более 20 метров от центральной линии. Соответственно, игрок находится в линии защиты, если он находится не более чем в 40 метрах от «своей» лицевой линии, и в линии нападения, если находится не более чем в 40 метрах от «чужой» лицевой линии.
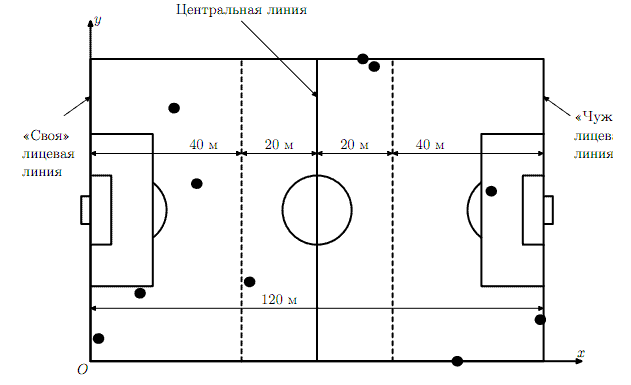
Например, в ситуации, изображенной на рисунке, в линии защиты находятся четыре игрока, в линии полузащиты — три, в линии нападения — также три.
В процессе игры некоторые игроки могут перемещаться из одной линии в другую. В этой задаче будем считать, что возможно перемещение из полузащиты в защиту (и обратно) и из полузащиты в нападение (и обратно). Таким образом, игрок, который в соответствии со схемой игры является защитником, не может оказаться в линии нападения, и наоборот — игрок, который в соответствии со схемой игры является нападающим, не может оказаться в линии защиты. Кроме этого, в соответствии с установкой тренера из каждой линии в каждую могло перейти не более двух игроков.
Ваша задача состоит в том, чтобы написать программу, которая по положениям игроков в некоторый момент времени найдет все возможные схемы игры, при которых в течение игры могло возникнуть такое расположение игроков.
Входной файл содержит десять строк, содержащих по два целых числа xi и yi каждая, — координаты каждого из игроков команды (0 ≤ xi ≤ 120, xi ≠ 40, xi ≠ 80, 0 ≤ yi ≤ 80).
В первой строке выходного файла выведите k — число схем игры, по которым может играть команда. В последующих k строках в произвольном порядке выведите описание каждой из этих схем. Следуйте формату данных, приведенному в примере.
97 0 13 18 2 6 119 11 42 21 72 80 75 78 106 45 22 67 28 47
9 2-5-3 3-5-2 3-4-3 4-5-1 4-4-2 4-3-3 5-4-1 5-3-2 5-2-3
В новой математической игре для одного игрока «Таблица чисел» используется таблица размером n строк на m столбцов, заполненная целыми числами. За один ход игрок выбирает одну из строк или один из столбцов и меняет знак на противоположный у всех чисел этой строки или столбца.
Цель игры состоит в том, чтобы привести таблицу в такой вид, что сумма чисел в каждой строке и каждом столбце является неотрицательной. При этом минимизировать количество ходов не требуется, но можно сделать не более 20000 ходов.
Ваша задача состоит в том, чтобы написать программу, которая по описанию начального вида таблицы, найдет последовательность ходов, которая ведет к достижению цели игры, или определит, что цель игры недостижима.
Первая строка входного файла содержит два целых числа: n и m (2 ≤ n, m ≤ 100). Каждая из последующих n строк содержит по m целых чисел a
В первой строке выходного файла выведите k — число ходов, которые необходимо выполнить, или «-1», если цели игры добиться невозможно. В первом случае в последующих k строках выведите описание этих ходов.
Описание каждого хода должно быть выведено в отдельной строке, которые должны содержать: тип хода («R» — на этом ходе выбирается строка или «C» — на этом ходе выбирается столбец) и номер соответствующей строки или столбца. Строки и столбцы нумеруются натуральными числами начиная с единицы, строки нумеруются сверху вниз, а столбцы — слева направо.
Выведенная вашей программой последовательность ходов должна содержать не более 20000 ходов. Гарантируется, что если существует последовательность ходов, ведущая к достижению цели игры, то существует и последовательность, удовлетворяющая указанному ограничению
2 2 -1 -3 1 -2
1 C 2
3 2 -1 -1 -1 -1 -1 -1
3 R 1 R 2 R 3
Компания «Замки и замки» недавно разработала новый тип кодового замка, для размещения на воротах замков. Панель замка представляет собой прямоугольник шириной w ячеек и высотой h ячеек. В некоторых из них расположены кнопки.
Код на этом замке вводится одновременным нажатием k кнопок. Для того, чтобы код было легче запомнить, используемые в нем кнопки должны образовывать связную область. Область называется связной, если из любой клетки области можно добраться до любой другой, перемещаясь только между клетками этой области с общей стороной. Важным критерием надежности замка является число различных кодов, которые на нем можно набрать.
Для оценки надежности замков требуется написать программу для вычисления указанной величины.
Формат входных данных
В первой строке входного файла находятся три целых числа h, w и k (1 ≤ h, w ≤ 30; 1 ≤ k ≤ 10). Каждая из последующих h строк содержит w символов. Символ «#» обозначает кнопку, а «.» — ее отсутствие.
Формат выходных данных
В выходной файл выведите единственное число — количество кодов, удовлетворяющих указанным требованиям.
Примеры
| Входные данные | Выходные данные |
| 2 2 2 .# ## | 2
|
| 5 6 7 .#.... ##.##. ..#.#. .####. .....# | 3 |
На рисунке изображен один из возможных кодов для второго примера.

У Индианы Джонса есть ключ от двери, ведущей к тайным богатствам инков. Ключ имеет форму правильного треугольника, который, в свою очередь, разбит на n2 маленьких правильных треугольников, в каждом из которых написана одна десятичная цифра. Пример ключа приведен ниже на рисунке.
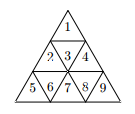
Джонс вставил треугольник в соответствующее треугольное отверстие в двери, и... она не открылась. Возможно, он вставил ключ неправильно, ведь его можно вставить тремя способами. Из-за того, что у Джонса осталась лишь одна попытка для того, чтоб открыть двери (в случае неудачи его убьют уже настигающие его кровожадные инки), он хочет знать как будет выглядеть ключ при его вставке в дверь другими двумя способами. После этого он сделает правильный выбор. Вас, как одного из двух своих помощников, он попросил показать ему только один из двух возможных вариантов. Внешний вид ключа, приведенного выше, при повороте против и по часовой стрелке изображен на рисунке ниже.
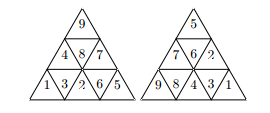
Поскольку вы не хотите смерти Индианы и хотите получить свою долю сокровищ, вам придется помочь ему!
В первой строке входного файла содержится одно целое число n (1 ≤ n ≤ 100). В следующих n строках описан сам треугольник. Строка входного файла, имеющая номер i + 1, содержит 2i - 1 цифру — содержание i-й строки ключа-треугольника.
Последняя строка содержит слово counterclockwise, если треугольник необходимо повернуть против часовой стрелки, и clockwise в противном случае.
Выведите вид ключа при его повороте в требуемую сторону. Треугольник опишите в том же формате, в котором это сделано во входном файле.
Решения, которые обрабатывают поворот только в одну сторону, будут оцениваться из 50 баллов.
3 1 2 3 4 5 6 7 8 9 counterclockwise
9 4 8 7 1 3 2 6 5
3 1 2 3 4 5 6 7 8 9 clockwise
5 7 6 2 9 8 4 3 1
В воинской части города Шатров продолжаются занятия по строевой подготовке. Молодой прапорщик Андрей Юрьевич уже приноровился проводить эти занятия, но тут его начальник Павел Андреевич стал давать ему новые, более сложные задания.
Как известно, обычно все солдаты выстраиваются в шеренгу по росту, начиная с самого низкого. Но Павлу Андреевичу это показалось слишком скучным и он потребовал от Андрея Юрьевича выстроить солдат в другом порядке. Случайный порядок ему показался слишком хаотичным, поэтому он потребовал построения, в котором будет ровно k инверсий. Инверсией называется такая пара солдат, что более высокий из них стоит в шеренге раньше более низкого.
К счастью для Андрея Юрьевича, все солдаты разного роста и для каждого он знает, какой он по росту среди всех солдат. Исходя из этого, каждому солдату Андрей Юрьевич присвоил номер: первый номер получил самый низкий, а последний — самый высокий солдат.
Например, в построении (3, 1, 2) есть две инверсии — пары (3, 1) и (3, 2), в которых более высокий солдат стоит раньше более низкого.
Андрей Юрьевич поручил Вам помочь ему в построении солдат в требуемом порядке, и для этого вы должны написать программу, находящую расстановку n солдат в порядке, в котором есть ровно k инверсий.
Первая и единственная строка входного файла содержит два целых числа n и k (1 ≤ n ≤ 100 000) — количество солдат в строю и требуемое количество инверсий.
Гарантируется, что существует построение солдат с требуемым числом инверсий, то есть 0 ≤ k ≤ n(n - 1) / 2.
В выходной файл выведите n целых чисел — построение солдат в требуемом порядке.
Решения, работающие при n ≤ 10, будут оцениваться из 30 баллов.
Решения, работающие при n ≤ 1000, будут оцениваться из 60 баллов.
3 2
3 1 2
3 0
1 2 3