Одним из способов контроля знаний учащихся является проведение тестирований. На тестировании обычно предлагается несколько вопросов, для каждого из которых необходимо выбрать один из вариантов ответа. Для этого тестируемому выдается специальный бланк с вопросами и вариантами ответов.

Тестирования можно проводить одновременно для достаточно большого количества людей, поэтому возникает вопрос об эффективной обработке заполненных тестируемыми бланков. Во Флатландии эту проблему пытаются решить с помощью применения информационных технологий для автоматической обработки результатов тестирования.

Первым этапом является написание программы, которая бы вычисляла баллы за тест по известной информации о правильных ответах на вопросы и ответах, данных тестируемым. Ваша задача состоит в написании такой программы.

Вася с Петей играют в следующую игру. Вася берет n картонных карточек, и на каждой из них с обеих сторон пишет по числу. После этого он выкладывает карточки в некотором порядке перед Петей. Пронумеруем карточки от 1 до n в том порядке, в котором их выложил Вася.

Петя пытается добиться того, чтобы последовательность чисел, написанных на карточках стала строго монотонной (возрастающей или убывающей). Для этого ему разрешается совершать следующие действия: выбрать два числа l и r, такие что 1 ≤ l≤ r ≤ n и перевернуть каждую из карточек от карточки номер l до карточки номер r.

Напомним, что последовательность c₁, . . . , c_n называется строго возрастающей, если выполняются неравенства c₁ < c₂ < … < c_n, и строго убывающей, если выполняются неравенства c₁ > c₂ > … > c_n.

Напишите программу, которая по описанию карточек определяет, какое минимальное число действий должен совершить Петя для того, чтобы добиться своей цели.

В тактике футбола одним из основных понятий является схема игры. Она определяет, сколько из десяти полевых игроков будут играть в защите, сколько — в полузащите и сколько — в нападении.

Например, схема игры 5-3-2 означает, что в команде пять защитников, три полузащитника и два нападающих. В соответствии с современными представлениями на схему игры накладываются следующие ограничения: должно быть не менее одного и не более пяти защитников, не менее одного и не более пяти полузащитников и не более трех нападающих. Отметим, что нападающих может в команде и не быть совсем. Будем рассматривать только такие схемы.

Будем считать, что футбольное поле имеет длину 120 метров и ширину 80 метров. Введем на нем прямоугольную декартову систему координат таким образом, как показано на рисунке. Ворота рассматриваемой нами команды находятся слева.

Будем также считать, что игрок в некоторый момент времени находится в линии полузащиты, если он находится на расстоянии не более 20 метров от центральной линии. Соответственно, игрок находится в линии защиты, если он находится не более чем в 40 метрах от «своей» лицевой линии, и в линии нападения, если находится не более чем в 40 метрах от «чужой» лицевой линии.

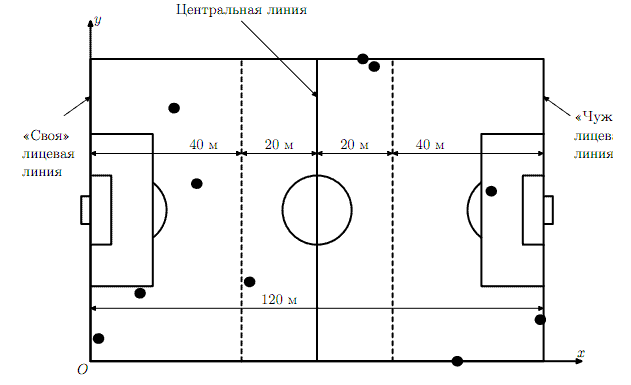
Например, в ситуации, изображенной на рисунке, в линии защиты находятся четыре игрока, в линии полузащиты — три, в линии нападения — также три.

В процессе игры некоторые игроки могут перемещаться из одной линии в другую. В этой задаче будем считать, что возможно перемещение из полузащиты в защиту (и обратно) и из полузащиты в нападение (и обратно). Таким образом, игрок, который в соответствии со схемой игры является защитником, не может оказаться в линии нападения, и наоборот — игрок, который в соответствии со схемой игры является нападающим, не может оказаться в линии защиты. Кроме этого, в соответствии с установкой тренера из каждой линии в каждую могло перейти не более двух игроков.

Ваша задача состоит в том, чтобы написать программу, которая по положениям игроков в некоторый момент времени найдет все возможные схемы игры, при которых в течение игры могло возникнуть такое расположение игроков.

На планете Руук существует Большая Корпорация Маленьких Фей. Одним из видов деятельности, которым испокон веков занимаются ее сотрудницы, является посадка грядок с волшебными грибами. Каждый день, начиная с самого первого дня существования этой корпорации, феи создают одну новую грядку грибов. После этого с новой грядки два дня можно собирать споры, которыми размножаются эти грибы, а потом грядка будет поставлять уже только сам продукт — грибы.

Таким образом, если обозначить количество грибов, посаженных на грядке, созданной в день номер i, как c_i, то оно будет считаться по формуле c_i = c_i - 1 + c_i - 2. Так, в первый и второй дни было посажено по одному грибу, в третий — два, в четвертый — три, в пятый — пять и так далее.

Волшебные грибы являются самыми ценными сувенирами, которые путешественник может привезти с планеты Руук. Поэтому первым, что делает любой приезжий, становится поиск грядки с волшебными грибами. Однако, в последнее время все чаще стали появляться сообщения о поддельных волшебных грибах. Тщательное расследование показало, что это является следствием действий Маленькой Корпорации Больших Фей, которая сажает грядки с грибами, внешне не отличимыми, но далеко не такими ценными, как волшебные. Причем, создавая очередную грядку, эти феи сажают туда такое количество грибов, какое их соперницы никогда не сажали и не смогут посадить.

Казалось бы, после выяснения этого факта отличать волшебные грядки от поддельных стало просто. Но обе корпорации существуют достаточно давно, количество грядок и грибов на них давно превысило все разумные пределы. Вас попросили написать программу, по количеству грибов на грядке сообщающую, является ли эта грядка волшебной.

Отряд Дамблдора готовится к полёту в Отдел Тайн Министерства Магии. Так как на их пути за Пророчеством могут встретиться слуги Волан-де-Морта, Гарри с Невиллом решили потренироваться в дуэльных боях.

Они решили провести \(n\) раундов дуэли, а после каждого раунда выпивать восстанавливающее зелье, чтобы не тратить лишних сил. Всего у ребят \(2n\) зелий. После каждого раунда дуэли они выбирают два наиболее близких по мощности восстанавливающих зелья. Из нескольких таких пар они выбирают ту, у которой сумма мощностей наибольшая. Затем Невилл выпивает более мощное зелье из пары, а Гарри - менее мощное.

Помогите Гарри с Невиллом определить, какие зелья и в каком порядке выпьет каждый из них.

1
3 6

6
3

2
11 43 56 22

22 56
11 43