2010(6 задач)
2011(6 задач)
2012(6 задач)
2013(6 задач)
XI Нижегородская городская олимпиада по информатике им. В. Д. Лелюха, 2015г.(6 задач)
XII Городская олимпиада школьников по информатике им. В. Д. Лелюха, 2016 г.(6 задач)
В секретном 240 отделе ИПФ РАН \(N\) сотрудников и \(N\) компьютеров. В отделе вводятся новые требования к секретности. В соответствии с этими требованиями, для каждого сотрудника будут определены ровно \(K\) компьютеров, к которым этот сотрудник будет иметь допуск (т.е. за которыми этот сотрудник будет иметь право работать), причём так, что к каждому компьютеру будут иметь допуск ровно \(K\) сотрудников.
Информация о том, какой сотрудник к какому компьютеру будет иметь допуск, будет известна лишь непосредственно перед вступлением новых требований в силу. Таким образом, чтобы не прерывать работу отдела, сотрудники должны будут быстро решить, кто за каким компьютером будет работать. Для этого им необходимо заранее написать программу, которая по любому распределению допусков сотрудников найдёт рассадку сотрудников по компьютерам, удовлетворяющую этим допускам.
Обратите внимание, что значение \(K\) тоже будет известно лишь в последний момент. Из общих соображений секретности известно лишь, что \(K\) будет равняться или 1, или 2, или 4; поэтому ваша программа должна уметь работать для любого из этих трех значений \(K\).
В первой строке входного файла записаны натуральные числа \(N\) и \(K\) (\(1\leq N \leq 500\)). Далее следуют \(KN\) строк, в каждой из которых записаны два натуральных числа — номер сотрудника и номер компьютера, к которому этот сотрудник имеет допуск.
Гарантируется, что каждый сотрудник имеет допуск ровно к \(K\) компьютерам, что к каждому компьютеру ровно \(K\) сотрудников имеют допуск, и что \(K\) равно либо 1, либо 2, либо 4.
В выходной файл выведите \(N\) строк, в каждой по два числа — номер сотрудника и номер компьютера, за которым он должен работать. Строки можно выводить в произвольном порядке.
Если есть несколько решений, выведите любое. Можно доказать, что для любого входного файла, удовлетворяющего указанным ограничениям, всегда имеется как минимум одно решение.
3 1 2 3 3 1 1 2
3 1 1 2 2 3
2 2 1 2 2 1 2 2 1 1
1 2 2 1
Жюри N-ской олимпиады по информатике решило зашифровать свои материалы подстановочным шифром. Для шифрования таким шифром задаётся взаимно-однозначное соответствие между буквами алфавита в открытом (т.е. до шифрования) тексте и буквами алфавита в закрытом (т.е. после шифрования) тексте, это соответствие и является ключом шифра. В процессе шифрования каждая буква в открытом тексте заменяется на соответствующую ей букву в закрытом тексте, порядок букв в слове при этом не меняется.
Однако, память у членов жюри оказалась уже не та, что в молодые годы, поэтому часто они путали, какие буквы надо было заменять на какие. В результате теперь они не могут восстановить свои материалы, а олимпиада уже на носу!
Чтобы разрешить свои проблемы, они обратились к вам. Для облегчения вашей задачи они выписали на бумажку все возможные варианты зашифрования букв, которые они могли применять, в виде набора пар «открытая буква» — «зашифрованная буква». Также вам известны все пары букв N-ского алфавита, которые могут следовать одна за другой в открытом тексте. Ваша задача состоит в том, чтобы по заданному зашифрованному слову сказать, соответствует ли ему хоть одно расшифрованное слово, единственен ли вариант расшифровки, и привести пример вариантов расшифровки слова. Слово \(\mathcal{A}\) считается возможной расшифровкой слова \(\mathcal{B}\), если, во-первых, его можно «зашифровать» (заменяя каждую букву на одну из соответствующих ей «зашифрованных» букв), получив слово \(\mathcal{B}\), и, во-вторых, каждая пара букв слова \(\mathcal{A}\), стоящих рядом, является допустимой для N-ского языка.
N-ский язык пользуется латинским алфавитом из 26 букв, регистр букв N-ское жюри не интересует, поэтому везде в открытом тексте используются большие буквы, а в закрытом — маленькие.
На первой строке входного файла находится одно целое число \(M\) (\(0 \leq M \leq 676\)) — число пар открытых — «зашифрованных» букв, указанных на бумажке, переданной N-ским жюри. Далее следуют \(M\) строк, на каждой находятся два символа — сначала открытая буква, потом вариант её «зашифрования». Пары не повторяются.
На следующей строке находится одно целое число \(K\) (\(0\leq K\leq 676\)) —
число пар открытых букв, которые могут идти одна за другой.
Далее следуют \(K\) строк, на каждой из которых по две открытые буквы, образующие
такую пару. Пары не повторяются. Заметим, что возможна ситуация, когда
последовательность букв “AB” в слове допустима,
а “BA” — нет, в этом случае
списке будет дана только пара “AB”, а пары “BA” не будет.
На следующей строке расположено одно целое число \(N\) (\(1 \leq N \leq 500\)) — длина зашифрованного слова, а на следующей строке — само слово (\(N\) маленьких латинских букв).
Может оказаться так, что какой-то открытой букве не соответствует ни одна «зашифрованная»; это означает, что эта буква в открытом тексте не использовалась.
Если вариантов дешифрования нет ни одного, в первую строку выходного файла
выведите “no”.
Если вариант дешифрования ровно один, в первую строку выходного файла
выведите “only”, а во вторую — дешифрованное слово.
Если вариантов дешифрования больше одного, в первую строку выходного файла
выведите “many”, а во вторую и третью — любые два
различных варианта дешифрования слова.
1 Uz 0 2 zz
no
1 Uz 0 1 z
only U
2 Uz Xz 3 UU XX XU 2 zz
many UU XU
7 Aa Az Ax Cz Dv Bx Bz 5 AB CA BC CB DE 4 zzxx
only BCAB
... но нужен ли на самом деле кому-нибудь 6\(1\over7\)-пунктовый шрифт, который на три четверти — шрифт Baskerville, и на четверть — Helvetica?
Дональд Э. Кнут. Идея Мета-фонта1
Маленькая девочка Оля добралась до полки, на которой стоят флаконы с мамиными любимыми духами, и начала заниматься своим любимым занятием — переливанием жидкостей из одного флакона в другой. Когда наконец мама застала её за этим занятием, прекрасная коллекция духов была уже безнадёжно утрачена.
К счастью, Оля — аккуратная девочка, поэтому все свои действия она записывала на бумажку. Помогите ей успокоить маму: определите, каков состав духов в первом (мамином любимом) флаконе, чтобы мама смогла придумать этой смеси новое название и рассказывать всем, какие прекрасные духи она смогла сделать вместе с дочерью.
Считайте, что Оля не пролила ни одной капли, а также что она тщательно встряхивала флаконы после каждого переливания. Учтите, что в маминых флаконах порой не видно, есть ли там жидкость, и потому Оля иногда могла пытаться переливать духи из пустого флакона (в результате, естественно, ничего не переливалось). Вы можете также считать, что после каждого переливания в каждом флаконе каждый тип духов либо полностью отсутствует, либо содержится в объеме не меньшем чем \(10^{-10}\).
На первой строке входного файла находятся два числа \(N\) и \(M\) — количество флаконов и число типов маминых любимых духов соответственно (\(2 \leq N \leq 100\); \(1 \leq M \leq 100\)). Далее следуют \(N\) строк, на \(i\)-ой из которых находятся два числа — тип \(L_i\) и объем \(V_i\) духов, находившихся изначально в \(i\)-ом флаконе (\(1\leq L_i \leq M\); \(0 \leq V_i \leq 1000\)). Возможно, что в нескольких флаконах находились духи одного и того же типа; возможно, что какого-то типа вообще не было на полке.
Далее во входном файле следует строка с числом \(K\) — количеством совершённых переливаний (\(1 \leq K \leq 1000\)). За ней следуют \(K\) строк, на \(k\)-ой из которых находятся три числа \(S_k\), \(T_k\) и \(A_k\) — номера флаконов, откуда и куда переливала Оля при \(k\)-ом переливании, и количество перелитой жидкости (в процентах от количества жидкости в \(S_k\)-ом флаконе перед переливанием). Гарантируется, что \(1\leq S_k,T_k\leq N\), что \(S_k\neq T_k\), и что \(0\leq A_k\leq 100\). Все числа во входном файле целые.
В выходной файл выведите \(M\) чисел — процентное содержание всех видов духов (от первого до \(M\)-ого) в первом флаконе после последнего переливания. Выводите результат с точностью не меньше двух знаков после запятой. Гарантируется, что после последнего переливания первый флакон оказался непустым.
1... but does anybody really need a 6\(1\over7\)-point font that is one fourth of the way between Baskerville and Helvetica? — Donald E. Knuth, The Concept of a Meta-Font
3 2 1 100 2 200 1 500 2 3 2 20 2 1 50
60.00 40.00
 Фирма, в которой всё ещё работает ваш друг, собирается расширяться на новые маршруты, и потому приобрела
новую площадку для ночного отстоя автобусов. Площадка раньше относилась к военной части, поэтому
она имеет необычную форму — форму треугольника, огороженного забором.
Фирма, в которой всё ещё работает ваш друг, собирается расширяться на новые маршруты, и потому приобрела
новую площадку для ночного отстоя автобусов. Площадка раньше относилась к военной части, поэтому
она имеет необычную форму — форму треугольника, огороженного забором.
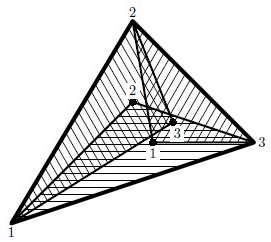
Для того, чтобы освещать площадку ночью, на ней надо установить несколько прожекторов. К счастью, у фирмы как раз в наличие есть три регулируемых прожектора, а на территории площадки обнаружились три высоких столба. Было решено на каждый столб повесить по прожектору и отрегулировать их так, чтобы каждый прожектор освещал ровно одну из трёх сторон забора: один прожектор должен освещать одну сторону забора, другой — другую, третий — третью. Никакой прожектор не должен освещать ни миллиметра “чужой” стены.
Конечно, прожекторы должны освещать не только забор, но вообще всю территорию площадки, поэтому возникла проблема: надо определить, какой прожектор на какую сторону забора направить. Зная ваши высокие навыки в решении подобных задач, фирма обратилась к вам за помощью. Напишите программу, которая будет решать эту задачу.
Естественно, каждый прожектор освещает не только стену, но и всю соответствующую часть двора — треугольник с вершиной в месте, где находится столб, на котором висит прожектор, и основанием, совпадающим с соответствующей стороной забора. Будем считать, что стороны этого треугольника тоже освещены прожектором. Тенью от столбов пренебрегайте.
Первая строка входного файла содержит одно число \(T\) — количество тестовых примеров, которые идут дальше (\(1\leq T\leq 1000\)).
Далее следуют описания \(T\) примеров. В каждом сначала идут шесть чисел \(x_1\), \(y_1\), \(x_2\), \(y_2\), \(x_3\), \(y_3\) — координаты вершин площадки, после чего идут шесть чисел \(X_1\), \(Y_1\), \(X_2\), \(Y_2\), \(X_3\), \(Y_3\) — координаты столбов. Гарантируется, что все столбы находятся строго внутри площадки. Гарантируется, что площадь площадки строго больше нуля. Гарантируется, что никакие два столба не совпадают. Все координаты во входном файле целые и не превосходят по модулю \(800\).
Выведите в выходной файл \(T\) строк по три числа в каждой: для каждого примера выведите номер стороны забора, на которую должен светить прожектор, находящийся на первом столбе, потом номер стороны, на которую должен светить прожектор со второго столба, и наконец номер стороны, на которую должен светить прожектор с третьего столба.
Первая сторона — та, которая соединяет вершины \((x_1, y_1)\) и \((x_2, y_2)\), вторая — \((x_2, y_2)\) и \((x_3, y_3)\), третья — \((x_3, y_3)\) и \((x_1, y_1)\).
Если решения не существует, выведите в соответствующую строку выходного файла три минус единицы:
“-1 -1 -1”.
Первый пример соответствует рисунку.
Среди тестов будут такие, в которых \(T\leq 10\); суммарная стоимость таких тестов будет 70 баллов.
2 0 0 6 10 12 4 7 4 6 6 8 5 -10 -10 0 10 10 -10 0 1 0 -1 1 1
2 3 1 3 2 1
Миша часто ездит в маршрутках. Миша законопослушный, поэтому он всегда покупает билет. Каждый билет в маршрутке имеет номер — \(2N\)-значное десятичное число, возможно, с ведущими нулями. После покупки билета Миша всегда проверяет, счастливый ли достался ему билет. Счастливым Миша считает такой билет, у которого сумма первых \(N\) цифр номера равна сумме последних \(N\) цифр. Если билет оказывается несчастливым, Миша ищет расстояние до ближайшего счастливого, т.е. минимальное число \(x\) такое, что если к номеру билета, полученного Мишей, прибавить или отнять \(x\) (при этом, разумеется, полученный номер должен быть корректным номером билета, т.е. должен быть не меньше нуля и не больше \(10^{2N}-1\)), то получившийся номер должен быть номером счастливого билета.
Билеты, у которых это расстояние максимально среди всех возможных, Миша называет совершенно несчастливыми. Мише очень интересно, сколько всего существует совершенно несчастливых билетов и какие номера у этих билетов. Но так как Миша плохо учился в школе, он не знает, как решать такую задачу, поэтому он обратился за помощью к вашему другу, специалисту по маршруткам. Он же перенаправил Мишу к вам.
Во входном файле содержится единственное число \(N\) (\(1 \leq N \leq 100\,000\)) — половина длины номера билетов.
В первой строке выходного выведите одно число \(k\) — количество совершенно несчастливых билетов. В последующих \(k\) строках выведите номера билетов в порядке возрастания. Номера нужно выводить с ведущими нулями, если таковые есть.
В примере расстояние от билета с номером 0050 до ближайшего счастливого равно 50: если из этого номера вычесть 50,
получится 0000 — счастливый номер. Аналогично, от билета 0051 расстояние до ближайшего счастливого тоже
равно 50: если к номеру прибавить 50, получится 0101. У билетов 9948 и 9949 расстояние до ближайшего
счастливого также равно 50; других билетов с таким расстоянием нет. Билетов с большим расстоянием тоже нет, поэтому эти четыре
билета и только они являются совершенно несчастливыми.
2
4 0050 0051 9948 9949