Темы --> Информатика --> Алгоритмы --> Алгоритмы на графах
    Кратчайшие пути в графе(116 задач)
    Обход в глубину(100 задач)
    Способы задания графа(54 задач)
    Минимальный каркас(12 задач)
    Потоки(21 задач)
    Паросочетания(17 задач)
    Эйлеров цикл(9 задач)
    Деревья(16 задач)
---> 74 задач <---
Источники --> Личные олимпиады
    Олимпиады сайта(17 задач)
    Школьная личная олимпиада ФМШ №2007 г. Москвы(7 задач)
    Золотая середина (Новосибирск)(10 задач)
    Нижегородская олимпиада школьников(42 задач)
    Московская олимпиада школьников(168 задач)
    Индивидуальная олимпиада по информатике и программированию (ИОИП)(22 задач)
    Открытая олимпиада школьников(173 задач)
    Украинские олимпиады(61 задач)
    Республиканская олимпиада школьников (Беларусь)(6 задач)
    Жаутыковские олимпиады(8 задач)
    Всероссийская олимпиада школьников(304 задач)
    Международные олимпиады(32 задач)
    Central European Olympiad in Informatics (4 задач)
    Интернет-олимпиады(2 задач)
    COCI(36 задач)
    Турнир Архимеда(36 задач)
    Baltic Olympiad in Informatics(10 задач)
Страница: 1 2 3 4 5 6 7 >> Отображать по:
#14
Сталкер
  
Темы: [0-1 BFS]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
128 megabytes

В городе Н при невыясненных обстоятельствах территория одного из заводов превратилась в аномальную зону. Все подъезды к территории были перекрыты, а сама она получила название промзоны. В промзоне находятся N зданий, некоторые из них соединены дорогами. По любой дороге можно перемещаться в обоих направлениях.

Начинающий сталкер получил задание добраться до склада в промзоне. Он нашел в электронном архиве несколько карт территории промзоны. Так как карты составлялись разными людьми, то на каждой из них есть информация только о некоторых дорогах промзоны. Одна и та же дорога может присутствовать на нескольких картах.

В пути сталкер может загружать из архива на мобильный телефон по одной карте. При загрузке новой карты предыдущая в памяти телефона не сохраняется. Сталкер может перемещаться лишь по дорогам, отмеченным на карте, загруженной на данный момент. Каждая загрузка карты стоит 1 рубль. Для минимизации расходов сталкеру нужно выбрать такой маршрут, чтобы как можно меньшее число раз загружать карты. Сталкер может загружать одну и ту же карту несколько раз, при этом придется заплатить за каждую загрузку. Изначально в памяти мобильного телефона нет никакой карты.

Требуется написать программу, которая вычисляет минимальную сумму расходов, необходимую сталкеру, чтобы добраться от входа в промзону до склада.

Входные данные

В первой строке входных данных содержатся два натуральных числа N и K (2 ≤ N ≤ 2000; 1 ≤ K ≤ 2000) — количество зданий промзоны и количество карт соответственно. Вход в промзону находится в здании с номером 1, а склад — в здании с номером N.

В последующих строках находится информация об имеющихся картах. Первая строка описания i-ой карты содержит число ri — количество дорог, обозначенных на i-ой карте. Затем идут ri строк, содержащие по два натуральных числа a и b (1 ≤ a, b ≤ N; a ≠ b), означающих наличие на i-ой карте дороги, соединяющей здания a и b. Суммарное количество дорог, обозначенных на всех картах, не превышает 300 000 (r1 + r2 + … + rK ≤ 300 000).

Выходные данные

Выведите одно число — минимальную сумму расходов сталкера. В случае, если до склада добраться невозможно, выведите число –1.

Примеры
Входные данные
12 4
4
1 6
2 4
7 9
10 12
3
1 4
7 11
3 6
3
2 5
4 11
8 9
5
3 10
10 7
7 2
12 3
5 12
Выходные данные
3
#15
Файловый менеджер
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Петя работает над очень большим проектом. Проект содержит N файлов. В процессе работы Пете часто приходится просматривать и редактировать файлы. Для ускорения работы Петя использует файловый менеджер Fur Manager, который отображает список имен файлов проекта в некотором порядке.

В текущей версии Fur Manager’a для перемещения по списку имен файлов есть следующие возможности:

  1. можно нажать клавишу вниз, при этом курсор перемещается на следующий файл в списке, для последнего файла следующим считается первый;

  2. можно нажать клавишу вверх, при этом курсор перемещается на предыдущий файл в списке, для первого файла предыдущим считается последний;

  3. можно нажать клавишу Alt и, удерживая ее, набрать последовательность латинских букв. После этого клавишу Alt следует отпустить, и в этот момент курсор переместится на ближайший файл, имя которого начинается c заданной последовательности символов. Ближайший файл — это файл, на который можно переместиться за наименьшее количество нажатий клавиши вниз. Если заданная последовательность является началом имени текущего файла, или файла, имя которого начинается с этой последовательности, не существует, то курсор останется на месте.

Первая и вторая из описанных возможностей файлового менеджера требуют по одному нажатию клавиши, а третья — одного нажатия (нажатие клавиши Alt) плюс количество нажатий, равное длине набранной последовательности латинских букв.

Файлы пронумерованы от 1 до N в порядке их следования. После загрузки Fur Manager’а курсор находится на первом файле.

Петя знает, что ему сначала придется редактировать файл с номером a1, затем с номером a2 и так далее, а последним — файл с номером ak. В последовательности a1, a2, ..., ak один и тот же номер может встречаться несколько раз. При каждом перемещении от одного файла к другому Петя хочет нажимать как можно меньше клавиш.

Требуется написать программу, которая выдает искомую последовательность нажатий клавиш.

Входные данные

В первой строке входных данных содержится целое число N (1 ≤ N ≤ 1000) — количество файлов в проекте.

В следующих N строках записаны имена файлов, по одному в каждой строке. Файлы перечислены в том порядке, в котором они отображаются файловым менеджером. Имена состоят только из строчных латинских букв. Длина каждого имени не превосходит 2000 символов. Все имена файлов различны.

Далее в следующей строке записано целое число k (1 ≤ k ≤ 10).

Последняя строка входных данных содержит k целых чисел a1, a2, ..., ak (1 ≤ ai ≤ N) — номера редактируемых файлов. Редактирование файлов выполняется в том порядке, в котором они встречаются в последовательности a1, a2, ..., ak.

Выходные данные

Выведите описание искомой последовательности нажатий клавиш в виде k блоков информации:

  • первый блок информации описывает перемещение от файла с номером 1 к файлу с номером a1;
  • второй блок информации описывает перемещение от файла с номером a1 к файлу с номером a2;
  • …
  • k-ый блок информации описывает перемещение от файла с номером ak–1 к файлу с номером ak.

Каждый блок информации выглядит следующим образом.

В первой строке блока записывается число L — наименьшее количество нажатий клавиш, необходимое для перемещения от очередного файла последовательности к следующему.

Следующие L строк блока описывают нажимаемые клавиши. Каждая из строк содержит описание одной клавиши:

  • если нажимается клавиша вниз, то в строке записывается слово down;
  • если нажимается клавиша вверх, то в строке записывается слово up;
  • если нажимается клавиша Alt, то в строке записывается слово Alt;
  • при нажатии клавиши с латинской буквой выводится соответствующая ей латинская буква.

Если существует несколько оптимальных способов перемещения, то требуется вывести любой из них.

Система оценки
  • Подзадача 1. Решения, верно работающие при \(n \leqslant 30\), оцениваются в 28 баллов. Баллы ставятся при прохождении всех тестов.
  • Подзадача 2. Решения, верно работающие при больших ограничениях, оцениваются по 4 балла за тест..
Примеры
Входные данные
6
a
b
c
d
e
f
4
4 3 1 6
Выходные данные
2
Alt
d
1
up
2
Alt
a
1
up
#21
Электрички на перегонах не меняют
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes

На пригородной железной дороге N станций и M соединяющих их перегонов. Любые две станции соединены не более чем одним перегоном. Сеть перегонов устроена так, что, отправившись от любой станции, можно вернуться на нее, только проехав хотя бы один перегон дважды. На железной дороге организовано движение электричек. Каждая электричка ходит в обоих направлениях по своему маршруту между двумя конечными станциями и останавливается на всех промежуточных станциях

Для удобства пассажиров руководство железной дороги решило ввести новую систему оплаты проезда. По этой системе каждой станции присваивается некоторое целое число, называемое тарифным номером этой станции. Стоимость проезда между двумя станциями без пересадок определяется модулем разности тарифных номеров этих станций. Тарифные номера станций вдоль маршрута каждой электрички должны изменяться монотонно, то есть при движении в каком-либо направлении строго возрастать и, следовательно, строго убывать при движении в обратном направлении. Это обеспечивает рост стоимости проезда с увеличением количества пройденных перегонов.

Требуется написать программу, которая назначит каждой станции тарифный номер.

1

4 станции, 3 перегона: 1-4, 2-4, 3-4

Маршруты: 1-4-2, 2-4-3, 3-4-1.


Ответ: решения нет

2

5 станций, 4 перегона: 1-5, 2-5, 3-5, 4-5

Маршруты: 1-5-2, 2-5-3, 3-5-4, 4-5-1.


Ответ: решение есть; например, следующее: номер станции: 1 2 3 4 5

тарифный номер: 1 4 1 5 3


Замечание: тарифные номера разных станций могут совпадать.
Входные данные

В первой строке входных данных содержатся два целых числа: N — количество станций (2 ≤ N ≤ 100 000), и M — количество перегонов между ними (1 ≤ M ≤ N – 1). В последующих M строках записаны пары целых чисел a, b (a ≠ b, 1 ≤ a ≤ N, 1 ≤ b ≤ N), означающие наличие перегона между станциями a и b. За ними в отдельной строке записано единственное целое положительное число K — количество маршрутов электричек. В последующих K строках идут описания маршрутов электричек, по одному на строке. Каждое описание представляет собой последовательность целых чисел — номеров всех станций маршрута в порядке одного из двух возможных направлений следования электрички. Описание маршрута заканчивается числом 0.

Все номера станций в описании маршрута различны. Количество станций в каждом маршруте не менее двух. Любые две последовательные станции в маршруте каждой электрички соединены перегоном. Суммарное количество станций в описаниях всех маршрутов не превосходит 200 000. Могут быть станции и перегоны, через которые не проходит ни одна электричка.

Выходные данные

В первую строку  выведите «NO», если искомого назначения тарифных номеров не существует. В противном случае в первую строку выведите «YES», а в следующей строке — N целых положительных чисел, где i-е число — тарифный номер i-й станции. Тарифный номер каждой станции должен находиться в диапазоне от 1 до N.

Если существует несколько решений, необходимо вывести любое из них.

Система оценивания

Тесты к этой задаче состоят из четырёх групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.

  • Группа 1 (20 баллов): N, K <= 20
  • Группа 2 (30 баллов): N, K <= 2000
  • Группа 3 (50 баллов): без дополнительных ограничений
Примеры
Входные данные
6 5
1 2
5 2 
5 6
4 5
3 2
6
1 2 0
5 6 0
3 2 1 0
5 2 3 0
4 5 2 0
6 5 4 0
Выходные данные
YES
2 3 4 1 2 3
#487
Монополия
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

В Тридесятом государстве есть N фирм, занимающихся разработкой программного обеспечения. Однажды известный олигарх Тридесятого государства Иванушка решил монополизировать эту отрасль. Для этого он хочет купить максимальное число программистских фирм Тридесятого государства.

Он разослал предложения всем N компаниям и через некоторое время получил от каждой их них согласие или отказ. Однако он знает, что в бизнесе очень многое зависит от взаимного доверия партнеров.

В результате небольшого исследования Иванушка установил, между какими компаниями существует взаимное доверие (причем всегда если компания доверяет компании B, то компания B доверяет компании A).

Теперь, при желании, Иванушка может повторно разослать предложения всем компаниям, включив в письма список компаний, давших согласие участвовать в его проекте. При этом каждая компания, независимо от своего первоначального мнения дает согласие, если в списке есть хотя бы одна компания, которой она доверяет, и отказ в противном случае. Таким образом, некоторые компании, которые изначально не согласились участвовать в проекте, могут теперь дать свое согласие, а некоторые из давших согласие — наоборот отказаться. В результате этого у Иванушки формируется новый список, который он опять может разослать фирмам. Он может сколь угодно долго повторять операцию, каждый раз рассылая текущий список. Иванушка может остановить процесс в любой момент и заключить договора с теми, кто после последней рассылки дал согласие.

Напишите программу, которая определит, какое максимальное число компаний может объединить Иванушка под своим началом.

Будем считать, что Иванушка — честный предприниматель и он никогда не подтасовывает рассылаемые им списки.

Входные данные

В первой строке входных данных содержится число N — количество фирм (1≤N≤2000). Далее идут N чисел, описывающих ответ фирмы на первое предложение Иванушки (1 — согласие, 0 — отказ). Далее задается число M (0≤M≤200000) — количество пар компаний, между которыми существует доверие. Далее следуют M пар чисел, задающих номера фирм, между которыми существует взаимное доверие (числа в паре не могут быть одинаковыми). Любая пара компаний упоминается в этом списке не более одного раза.

Выходные данные

Выведите  одно число — максимальное число фирм, которое сможет купить Иванушка.

Примеры
Входные данные
7
1 0 0 0 0 0 1
6
1 2
1 3
1 4
4 5
5 6
2 5
Выходные данные
4
Входные данные
3
0 0 0
0
Выходные данные
0
#493
Формула - 3
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Топологическая сортировка

В ежегодном чемпионате Флатландии (которая, естественно, является плоским миром) по космическим гонкам "Формула-3" участвуют N космических скутеров, имеющие форму треугольников. До начала гонок скутеры занимают положение в стартовой зоне согласно результатам жеребьевки.

1

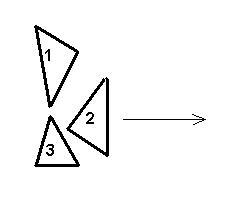
Скутеры стартуют строго по порядку. Каждый скутер,получив команду «старт», уезжает в положительном направлении оси Ox. Следующий скутер стартует лишь тогда, когда предыдущий покинет стартовую зону. Скутеры уезжают строго параллельно оси Ox, скутеры в стартовой зоне не поворачивают и не разворачиваются.

Естественно, что если в момент старта на пути скутера окажется другой скутер, то произойдет авария (даже если скутер заденет лишь угол другого скутера своим углом).

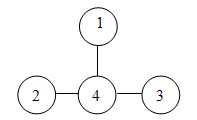
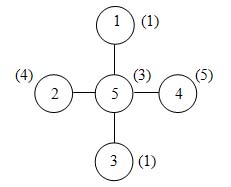
Для уменьшения опасности столкновения скутеров на старте строго соблюдается следующее правило: прямые, параллельные оси Ox и пересекающие какой-то скутер, должны в совокупности пересекать не более 100 других скутеров (прямая, проходящая через одну точку скутера также считается прямой, пересекающей скутер). Например, на приведенном рисунке прямые, параллельные Ox и пересекающие скутер 2, проходят через 2 других скутера (1 и 3), а прямые, проходящие через скутер 1, проходят только через один другой скутер (номер 2).

Главный Судья гонок хочет определить порядок, в котором должны стартовать скутеры, чтобы аварии не произошло. Например, в ситуации, приведенной на рисунке, сначала должен стартовать скутер номер 2 (если попытается стартовать скутер номер 1 или 3, то он столкнется со скутером номер 2). После этого скутеры 1 и 3 могут стартовать в любом порядке (они друг другу не мешают).

Помогите Главному Судье — напишите программу, которая определит какой-нибудь порядок старта скутеров, чтобы аварии не произошло.

Входные данные

В первой строке вводится натуральное число N( 1 ≤ N ≤ 30 000).

В каждой из следующих N строк содержится по 6 чисел: x1, y1, x2, y2, x3, y3 – координаты трех вершин скутера на старте, целые числа, не превосходящие по модулю 106. В начальный момент скутеры не задевают друг друга.

Выходные данные

Выведите через пробел N чисел – номера скутеров в том порядке, в котором они могут стартовать. Если решений несколько, выведите одно любое из них. Если решений нет, выведите одно число -1.

Примечание: первый тест соответствует приведенному рисунку. Ответ 2 3 1 в этом тесте также является правильным

Примеры
Входные данные
3
1 19 3 9 6 15
5 6 10 2 10 12
1 1 6 1 3 7
Выходные данные
Входные данные
3
0 1 -2 1 -1 -1
5 6 10 2 10 12
1 1 6 1 3 7


Выходные данные

                            
                                


                        

                    

                

                
        

            Страница: 
                    1
                    2
                    3
                    4
                    5
                    6
                    7
                >>
            Отображать по:
            
        

    
            

        

        
    
    

    

        

            
Выбрано
:
            
Отменить
|
            
Добавить в контест