Темы --> Информатика --> Алгоритмы --> Вычислительная геометрия
    Градиентный спуск(1 задач)
    Элементарная геометрия(144 задач)
    Многоугольники. Выпуклые оболочки(38 задач)
    Клеточная геометрия(8 задач)
    Квадродерево(3 задач)
---> 55 задач <---
Источники --> Личные олимпиады
    Олимпиады сайта(17 задач)
    Школьная личная олимпиада ФМШ №2007 г. Москвы(7 задач)
    Золотая середина (Новосибирск)(10 задач)
    Нижегородская олимпиада школьников(42 задач)
    Московская олимпиада школьников(168 задач)
    Индивидуальная олимпиада по информатике и программированию (ИОИП)(22 задач)
    Открытая олимпиада школьников(173 задач)
    Украинские олимпиады(61 задач)
    Республиканская олимпиада школьников (Беларусь)(6 задач)
    Жаутыковские олимпиады(8 задач)
    Всероссийская олимпиада школьников(304 задач)
    Международные олимпиады(32 задач)
    Central European Olympiad in Informatics (4 задач)
    Интернет-олимпиады(2 задач)
    COCI(36 задач)
    Турнир Архимеда(36 задач)
    Baltic Olympiad in Informatics(10 задач)
Страница: << 5 6 7 8 9 10 11 >> Отображать по:
#3209
Дом у дороги
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Пересечение полуплоскостей за O(NlogN)

Министерство дорожного транспорта решило построить себе новый офис. Поскольку министр регулярно выезжает с инспекцией наиболее важных трасс, было решено, что офис министерства не должен располагаться слишком далеко от них.

Наиболее важные трассы представляют собой прямые на плоскости. Министерство хочет выбрать такое расположение для своего офиса, чтобы максимум из расстояний от офиса до трасс был как можно меньше.

Требуется написать программу, которая по заданному расположению наиболее важных трасс определяет оптимальное расположение дома для офиса министерства дорожного транспорта.

Входные данные

Первая строка входного файла содержит одно целое число \(n\) — количество наиболее важных трасс (\(1 \le n \le 10^4\)).

Последующие \(n\) строк описывают трассы. Каждая трасса описывается четырьмя целыми числами \(x_1\), \(y_1\), \(x_2\) и \(y_2\) и представляет собой прямую, проходящую через точки \((x_1, y_1)\) и \((x_2, y_2)\). Координаты заданных точек не превышают по модулю \(10^4\). Точки \((x_1, y_1)\) и \((x_2, y_2)\) ни для какой прямой не совпадают.

Выходные данные

Выходной файл должен содержать два разделенных пробелом вещественных числа: координаты точки, в которой следует построить офис министерства дорожного транспорта. Координаты по модулю не должны превышать \(10^9\), гарантируется, что хотя бы один такой ответ существует. Если оптимальных ответов несколько, необходимо выведите любой из них.

Ответ должен иметь абсолютную или относительную погрешность не более \(10^{-6}\), что означает следующее. Пусть максимальное расстояние от выведенной точки до некоторой трассы равно \(x\), а в правильном ответе оно равно \(y\). Ответ будет засчитан, если значение выражения \(|x - y| / max(1, |y|)\) не превышает \(10^{-6}\).

Примечание

Правильные решения для тестов, в которых \(n \le 100\) и все прямые параллельны, оцениваются из 20 баллов.

Правильные решения для тестов, в которых \(n \le 100\) и все прямые параллельны осям координат, оцениваются из 20 баллов.

Правильные решения для тестов, в которых \(n \le 100\), оцениваются из 70 баллов (в эти баллы включаются также по 20 баллов за случаи, описанные в предыдущих двух абзацах).

Примеры
Входные данные
4
0 0 0 1
0 0 1 0
1 1 2 1
1 1 1 2
Выходные данные
0.5000000004656613 0.4999999995343387
Входные данные
7
376 -9811 376 -4207
6930 -3493 6930 -8337
1963 -251 1963 -5008
-1055 9990 -684 9990
3775 -348 3775 1336
7706 -2550 7706 -8412
-9589 8339 -4875 8339
Выходные данные
4040.9996151750674 12003.999615175067
#3294
Параллелограмм (6-9)
  

На уроке геометрии семиклассники Вася и Петя узнали, что такое параллелограмм. На перемене после урока они стали играть в игру: Петя называл координаты четырех точек в произвольном порядке, а Вася должен был ответить, являются ли эти точки вершинами параллелограмма.

Вася, если честно, не очень понял тему про параллелограммы, и ему требуется программа, умеющая правильно отвечать на Петины вопросы.

Напомним, что параллелограммом называется четырехугольник, противоположные стороны которого равны и параллельны.

Входные данные

В первой строке входного файла записано целое число \(N\) (\(1 \leq N \leq 10\)) - количество заданных Петей вопросов. Каждая из \(N\) последующих строк содержит описание четырех точек - четыре пары целых чисел \(X\) и \(Y\) (\(-100 \leq X\leq 100\), \(-100\leq Y \leq 100\)), обозначающих координаты точки. Гарантируется, что четыре точки, о которых идет речь в одном вопросе, не лежат на одной прямой.

Выходные данные

Для каждого из вопросов выведите "YES", если четыре заданные точки могут образовать параллелограмм, и "NO" в противном случае. Ответ на каждый из запросов должен быть в отдельной строке без кавычек.

Примеры
Входные данные
3
1 1 4 2 3 0 2 3
1 1 5 2 2 3 3 0
0 0 5 1 6 3 1 2
Выходные данные
YES
NO
YES
#3337
Забор
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

На одну Очень Известную Планету упал метеорит. Метеорит в атмосфере распался на \(N\) кусков, каждый из которых упал в свою точку.

Чтобы куски метеорита не были испорчены любопытными туристами, для проведения научных исследований решили построить один забор, которым огородить не менее \(K\) кусков метеорита. Естественно, что забор должен быть минимально возможной длины, и внутри него должны оказаться любые \(K\) (или больше) кусков метеорита (кусок считается лежащим внутри забора как когда он лежит строго внутри, так и когда забор проходит непосредственно через него).

Конечно, ученые хотят огородить как можно больше кусков, но как всегда, все упирается в деньги. Главный бухгалтер решил составить такую таблицу: для каждого \(K\) от 1 до \(N\) определить, какой минимальной длины нужно построить забор, чтобы внутри него оказалось не менее \(K\) кусков метеорита. Помогите ему.

Входные данные

В первой строке входного файла записано единственное целое число \(N\). В каждой из следующих \(N\) строк записано по паре целых чисел, по модулю не превосходящих \(1\,000\) - координаты точек, куда упали куски метеорита. Никакие два куска не упали в одну и ту же точку.

Выходные данные

Выведите \(N\) чисел, \(i\)-е (\(1 \le i \le N\)) должно быть равно минимальной длине забора, внутри которого окажется не менее \(K\) кусков метеорита. Выведенный ответ будет сравниваться с правильным с точностью до \(10^{-6}\).

Примечания

Тесты состоят из четырёх групп.

  1. Тесты 1--2, из условия, оцениваются в 0 баллов.
  2. В тестах этой группы \(1 \le N \le 16\). Эта группа оценивается в 30 баллов, при этом баллы начисляются только при прохождении всех тестов группы.
  3. В тестах этой группы \(1 \le N \le 30\). Эта группа также оценивается в 30 баллов, баллы начисляются только при прохождении всех тестов группы.
  4. Offline-группа. Баллы за тесты этой группы начисляются только при прохождении всех тестов 1-й и 2-й групп. Тесты объединяются в подгруппы, каждая из которых оценивается в 10 баллов, баллы за каждую подгруппу начисляются только при прохождении всех тестов подгруппы. Подгруппы соответствуют ограничениям \(N \le 40\), \(N \le 60\), \(N \le 80\), \(N \le 100\).

Примеры
Входные данные
4
0 0
0 1
1 0
1 1
Выходные данные
0.000000000
2.000000000
3.414213562
4.000000000
Входные данные
3
1 1
0 0
2 0
Выходные данные
0.000000000
2.828427125
4.828427125
#3400
Распил бревен
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Лесопильный комбинат выполняет заказ на распил брусьев для строительства детского городка. Все готовые брусья должны иметь форму треугольных призм, основаниями которых являются равнобедренные треугольники. Для изготовления брусьев закуплены заготовки в виде половинок продольно распиленных бревен. Заготовки не являются идеальными половинками цилиндров, поэтому при изготовлении бруса необходимо учитывать форму заготовок. Комбинат заинтересован в изготовлении бруса с наибольшей возможной площадью поперечного сечения.

Для каждой заготовки измеряется несколько сечений. Каждое из них задано в виде ломаной, представленной координатами ее вершин (\(x_0, y_0\)), (\(x_1, y_1\)), ..., (\(x_N, y_N\)) в порядке их следования. Координаты вершин ломанной удовлетворяют следующим условиям:

\(x_0 < x_1 < x_2 < \dots < x_N\);

\(x_i = 0\) для некоторого \(0 < i < N\);

\(y_0 = y_N = 0\);

\(y_0 = y_N = 0\);

для всех \(i\) от 1 до (\(N – 1\)) выполнено условие \(y_i > 0\).

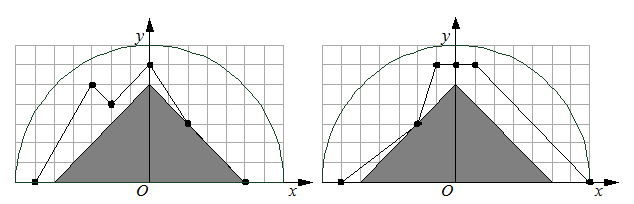
С учетом описанных требований необходимо найти максимально возможную площадь равнобедренного треугольника, удовлетворяющего следующим условиям:

основание треугольника лежит на оси абсцисс;

основание симметрично относительно начала координат;

треугольник полностью лежит внутри каждого из измеренных сечений заготовки.

Требуется написать программу, которая по заданным сечениям заготовки вычислит максимально возможную площадь искомого равнобедренного треугольника.

Входные данные

Первая строка входного файла содержит целое число \(K\) – количество измеренных сечений.

Далее следуют описания каждого из \(K\) сечений. В первой строке описания сечения содержится число \(N_K\) – количество звеньев ломаной. За ней следуют (\(N_K + 1\)) строк, каждая из которых содержит пару целых чисел \(x_i\) и \(y_i\) – координаты вершин ломаной сечения в порядке их следования.

Выходные данные

Выходной файл должен содержать одно вещественное число – наибольшую возможную площадь треугольника. Эта площадь должна иметь абсолютную или относительную погрешность не более \(10^{–6}\), что означает следующее. Пусть выведенное число равно \(x\), а в правильном ответе оно равно \(y\). Ответ будет считаться правильным, если значение выражения \(|x – y| / max(1, |y|)\) не превышает \(10^{–6}\).

Подзадачи и система оценки

Данная задача содержит пять подзадач.

Подзадача 1 (20 баллов)

\(K = 1\), \(N_1 \leq 15\), координаты вершин по модулю не превышают 20.

Для оценки данной подзадачи используется соответствующая группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

Подзадача 2 (10 баллов)

\(1 \leq K \leq 20\), сумма \(N_i \leq 2000\), координаты вершин по модулю не превышают \(10^4\). Гарантируется, что полученный в качестве ответа треугольник является прямоугольным.

Для оценки данной подзадачи используется соответствующая группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

Подзадача 3 (20 баллов)

\(1 \leq K \leq 20\), сумма \(N_i \leq 2000\), координаты вершин по модулю не превышают \(10^4\).

Для оценки данной подзадачи используется соответствующая группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

Подзадача 4 (10 баллов)

\(1 \leq K \leq 1000\), сумма \(N_i \leq 10^5\), координаты вершин по модулю не превышают \(10^9\). Гарантируется, что полученный в качестве ответа треугольник является прямоугольным.

Для оценки данной подзадачи используется соответствующая группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

Подзадача 5 (40 баллов)

\(1 \leq K \leq 1000\), сумма \(N_i \leq 10^5\), координаты вершин по модулю не превышают \(10^9\).

Каждый тест для данной подзадачи оценивается отдельно.

Примеры
Входные данные
2
5
-6 0
-3 5
-2 4
0 6
2 3
5 0
5
-6 0
-2 3
-1 6
0 6
1 6
7 0
Выходные данные
25.0
#3870
Космический кегельбан
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

На планете Плюк открылся новый космический кегельбан. Поле для кегельбана представляет собой бесконечную плоскость, на которой расставлены кегли.

Каждая кегля представляет собой высокий цилиндр с основанием в виде круга радиусом r метров. Все кегли одинаковые. Кегли расставлены по следующим правилам. Кегли образуют n рядов, в первом ряду стоит одна кегля, во втором — две, и так далее. В последнем n-м ряду стоит n кеглей. Введем на плоскости систему координат таким образом, чтобы единица измерения была равна одному километру. Центр единственной кегли в первом ряду находится в точке (0, 0). Центры кеглей во втором ряду находятся в точках (–1, 1) и (1, 1). Таким образом, центры кеглей в i-м ряду находятся в точках с координатами (–(i – 1), i –  1), (–( i – 3), i – 1), …, (i – 1, i – 1).

Игра происходит следующим образом. Используется шар с радиусом q метров. Игрок выбирает начальное положение центра шара (xc,  yc) и вектор направления движения шара (vx, vy). После этого шар помещается в начальную точку и двигается, не останавливаясь, в направлении вектора (vx, vy). Считается, что шар сбил кеглю, если в процессе движения шара имеет место ситуация, когда у шара и кегли есть общая точка. Сбитые кегли не меняют направления движения шара и не сбивают соседние кегли при падении.

На рисунке приведен пример расположения кеглей для r = 500, n = 4 и шара для q = 1000, xc = –2, yc = –2, vx = 1, vy = 1.

Требуется написать программу, которая по заданным радиусу кегли r, количеству рядов кеглей n, радиусу шара q, его начальному положению ( xc, yc) и вектору направления движения (vx,  vy) определяет количество кеглей, сбитых шаром.

Входные данные

Первая строка входного файла содержит два целых числа: r и n, разделенных ровно одним пробелом (1 ≤ r ≤ 700, 1  ≤ n ≤ 200 000).

Вторая строка входного файла содержит целое число q (1  ≤ q ≤ 109).

Третья строка входного файла содержит два целых числа xc и yc, разделенных ровно одним пробелом (–106≤ xc ≤ 106, –10 6≤ yc, 1000 ×yc < –(r + q) ).

Четвертая строка входного файла содержит два целых числа vx и vy, разделенных ровно одним пробелом (–106≤ vx ≤ 106, 0  < vy ≤ 106).

Выходные данные

Выходной файл должен содержать одно целое число — количество сбитых кеглей.

Примечание

Рисунок ниже показывает, какие кегли будут сбиты (такие кегли обозначены «х»).

Система оценки

Потестовая.

Примеры
Входные данные
500 4
1000
-2 -2
1 1
Выходные данные
7
Страница: << 5 6 7 8 9 10 11 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест