Страница: 1 Отображать по:

#571

Реки

Темы: [Динамическое программирование на графах]

Источники: [ Личные олимпиады, Международные олимпиады, 2005, 2 тур, Задача C ]

Почти все Королевство Байтленд покрыто лесами и реками. Малые реки сливаются в более крупные реки, которые, в свою очередь, сливаются друг с другом; в конечном счете, все реки сливаются вместе в одну большую реку. Большая река впадает в море вблизи города Байттаун.

В Байтленде имеется n лесозаготовительных поселков, каждый из которых расположен вблизи какой-либо реки. В настоящее время в Байттауне находится большая пилорама, которая обрабатывает все деревья, срубленные в Королевстве. Деревья сплавляются вниз по рекам от поселков, где они срублены, к пилораме в Байттауне. Король Байтленда решил поставить k дополнительных пилорам в поселках, чтобы уменьшить стоимость сплава деревьев. После установки пилорам деревья не обязательно должны сплавляться в Байттаун, а могут быть обработаны на ближайшей пилораме, находящейся ниже по течению рек. Очевидно, что деревья, срубленные в окрестности поселка с пилорамой, вообще не сплавляются по рекам.

Необходимо отметить, что реки в Байтленде не разветвляются. Из этого следует, что для каждого поселка существует единственный путь сплава деревьев вниз по течению рек от него в Байттаун.

Королевские счетоводы подсчитали количество деревьев, срубаемых в каждом поселке за год. Вам необходимо определить, в каких поселках следует установить пилорамы, чтобы минимизировать общую стоимость сплава деревьев за год. Стоимость сплава одного дерева составляет один цент за каждый километр пути.

Задание

Напишите программу, которая:
<> * читает из стандартного ввода количество поселков, количество дополнительных пилорам, которые будут установлены, количество срубленных в каждом поселке деревьев и описание рек,
*вычисляет минимальную стоимость сплава деревьев после установки дополнительных пилорам,
*выводит результат в стандартный вывод.

Входные данные

Первая строка входных данных содержит два целых числа: $n$ — количество поселков, не считая Байттауна (2 ≤ $n$ ≤ 100), и $k$ — количество дополнительных пилорам, которые будут установлены (1 ≤ $k$ ≤ 50 и $k$ ≤ $n$ ). Поселки нумеруются числами 1 , 2 , ...., n , а Байттаун имеет номер 0.

Каждая из последующих n строк содержит три целых числа, разделенных одним пробелом. Строка i + 1 содержит:

$w_i$ — количество деревьев, срубаемых в поселке $i$ за год (0 ≤ $w_i$ ≤ 10 000),
$v_i$ — ближайший поселок (либо Байттаун) вниз по реке от поселка $i$ (0 ≤ $v_i$ ≤ $n$ ),
$d_i$ — расстояние (в километрах) по реке от поселка $i$ до поселка $v_i$ (1 ≤ $d_i$ ≤ 10 000).
Гарантируется, что суммарная стоимость сплава всех деревьев к пилораме в Байттауне не превосходит 2 000 000 000 центов в год.
В 50% тестов число n не превосходит 20.

Выходные данные

Первая и единственная строка выходных данных должна содержать одно целое число: минимальную стоимость сплава (в центах).

Пояснения

Рисунок сверху иллюстрирует входные данные примера. Номера поселков указаны внутри кругов. Числа под кругами обозначают количество деревьев, срубаемых вблизи данного поселка. Числа над стрелками указывают длины рек.

Пилорамы должны быть установлены в поселках 2 и 3.

Примеры

Входные данные

Выходные данные

#1012

Деревни

Темы: [Динамическое программирование на графах]

Источники: [ Личные олимпиады, Открытая олимпиада школьников, 2002, Задача I ]

В тридесятом государстве есть N деревень. Некоторые пары деревень соединены дорогами. В целях экономии, «лишних» дорог нет, т.е. из любой деревни в любую можно добраться по дорогам единственным образом.

Новейшие исследования показали, что тридесятое государство находится в сейсмически опасной зоне. Поэтому глава государства захотел узнать, какой именно ущерб может принести его державе землетрясение. А именно, он хочет узнать, какое минимальное число дорог должно быть разрушено, чтобы образовалась изолированная от остальных группа ровно изP деревень такая, что из любой деревни из этой группы до любой другой деревни из этой группы по-прежнему можно будет добраться по неразрушенным дорогам (группа изолирована от остальных, если никакая неразрушенная дорога не соединяет деревню из этой группы с деревней не из этой группы).

Вы должны написать программу, помогающую ему в этом.

Входные данные

Первая строка входного файла содержит два числа: N и P (1≤P≤N≤150). Все остальные строки содержат описания дорог, по одному на строке: описание дороги состоит из двух номеров деревень (от 1 до N), которые эта дорога соединяет. Все числа во входном файле разделены пробелами и/или переводами строки.

Выходные данные

В выходной файл выведите единственное число – искомое количество дорог.

Примеры

Входные данные

Выходные данные

#1044

Лотерея

Темы: [Динамическое программирование на графах] [Бор]

Источники: [ Личные олимпиады, Открытая олимпиада школьников, 2005, Задача J ]

На одном из телеканалов каждую неделю проводится следующая лотерея. В течение недели участники делают свои ставки. Каждая ставка заключается в назывании какого-либо $M$-значного числа в системе счисления с основанием $K$ (то есть, по сути, каждый участник называет $M$ цифр, каждая из которых лежит в диапазоне от 0 до $K-1$). Ведущие нули в числах допускаются.

В некоторый момент прием ставок на текущий розыгрыш завершается, и после этого ведущий в телеэфире называет выигравшее число (это также $M$-значное число в $K$-ичной системе счисления). После этого те телезрители, у кого первая цифра их числа совпала с первой цифрой числа, названного ведущим, получают выигрыш в размере $A_1$ рублей. Те, у кого совпали первые две цифры числа — получают $A_2$ рублей (при этом если у игрока совпала вторая цифра, но не совпала первая, он не получает ничего). Аналогично угадавшие первые три цифры получают $A_3$ рублей. И так далее. Угадавшие все число полностью получают $A_m$ рублей. При этом если игрок угадал $t$ первых цифр, то он получает $A_t$ рублей, но не получает призы за угадывание $t-1$, $t-2$ и т.д. цифр. Если игрок не угадал первую цифру, он не получает ничего.

Напишите программу, которая по известным ставкам, сделанным телезрителями, находит число, которое должна назвать телеведущая, чтобы фирма-организатор розыгрыша выплатила в качестве выигрышей минимальную сумму. Для вашего удобства ставки, сделанные игроками, уже упорядочены по неубыванию.

Входные данные

В первой строке задаются числа $N$ (количество телезрителей, сделавших свои ставки, $1\le N\le 100000$), $M$ (длина чисел $1\le M\le 10$) $K$ (основание системы счисления $2\le K\le 10$). В следующей строке записаны $M$ чисел $A_1$, $A_2$, ..., $A_M$, задающих выигрыши в случае совпадения только первой, первых двух,... , всех цифр ($1\le A_1\le A_2\le ... \le A_M\le 100000$). В каждой из следующих $N$ строк записано по одному $M$-значному $K$-ичному числу. Числа идут в порядке неубывания.

Выходные данные

В первой строке выведите искомое число (если решений несколько — выведите любое из них), а во второй строке — сумму, которую при назывании телеведущей первого числа придется выплатить в качестве выигрыша.

Примеры

Входные данные

Выходные данные

011
6

Входные данные

1 1 10
100
0

Выходные данные

1
0

#111495

Столицы

Темы: [Динамическое программирование на графах] [Обход в глубину]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2013, 2 день, Задача D ]

В стране Триландии близятся выборы новых столиц. Столицы в Триландии необычные, поскольку ими являются одновременно сразу три различных города. Такая идея размещения столиц основана на исследованиях эффективности управления страной, выполненных ведущими экономистами Триландии.

Всего в Триландии n городов, из которых некоторые пары городов соединены дорогами, и по каждой из них можно проехать в обе стороны. Время проезда по каждой дороге в одну сторону равно одному часу. При этом все города соединены дорогами таким образом, что из каждого города можно добраться в любой другой, причем это можно сделать единственным способом, если по каждой дороге проезжать не более одного раза и только в одну сторону.

Как показали результаты проведенных триландскими экономистами исследований, управление страной будет наиболее эффективным, если три столицы будут выбраны так, что время кратчайшего пути между каждой парой столиц составит ровно d часов. Перед проведением выборов необходимо знать, сколько существует различных троек городов, удовлетворяющих описанным выше свойствам. Две тройки городов считаются различными, если в первой тройке есть хотя бы один город, которого нет во второй тройке, и наоборот.

Требуется написать программу, которая по количеству городов в Триландии и описанию дорог находит количество троек городов, которые могут быть столицами.

Входные данные

Первая строка входного файла содержит два разделенных пробелом целых числа: количество городов в Триландии n и требуемое время в пути между столицами d ($3 \leq n \leq 10^5$, $1 \leq d < n$). Каждая из последующих (n – 1) строк содержит описание одной дороги: пару разделенных пробелом различных целых чисел $a_i$ и $b_i$ — номера городов, которые соединены двусторонней дорогой ($1 \leq a_i \leq n$, $1 \leq b_i \leq n$, $a_i \ne b_i$). Каждая пара городов соединена не более чем одной дорогой.

Выходные данные

Выходной файл должен содержать одно целое число — количество подходящих троек городов, которые могут быть выбраны столицами. В случае, если нужных троек городов не окажется, выходной файл должен содержать ноль.

Пояснения к тестам

В первом примере существует единственный способ выбрать три столицы: города под номерами 2, 3 и 4. Рисунок, соответствующий первому примеру, приведен ниже.

$\text{[math]}$

Во втором примере существует четыре варианта выбора трёх столиц из четверки городов: 2, 3, 4 и 5. Можно также выбрать столицами города с номерами 1, 6 и 7. Рисунок, соответствующий второму примеру, приведен ниже.

$\text{[math]}$

Система оценивания

Правильные решения для тестов, в которых 3 ≤ n ≤ 50, будут оцениваться из 20 баллов.

Правильные решения для тестов, в которых 3 ≤ n ≤ 500, будут оцениваться из 40 баллов.

Правильные решения для тестов, в которых 3 ≤ n ≤ 5000, будут оцениваться из 60 баллов.

Примеры

Входные данные

Выходные данные

Входные данные

Выходные данные

#111502

Автостанции

Темы: [Обход в глубину] [Динамическое программирование на графах]

Источники: [ Личные олимпиады, Нижегородская олимпиада школьников, 2009, Задача C ]

Фирма, в которой работает ваш друг, решила воспользоваться удобным моментом и купила компанию, занимающуюся пригородными автобусными пассажирскими перевозками. Таким образом, фирма вашего друга расширяет область деятельности и будет теперь обслуживать и некоторые внутриобластные автобусные маршруты.

Сейчас руководство фирмы, и в том числе ваш друг, заняты оптимизацией работы этих маршрутов. Одна из основных проблем, которые были обнаружены, состоит в том, что большинство автобусов, использующихся там, очень старые и изношенные, и поэтому часто выходят из строя. В целях улучшения ситуации было принято решение о создании сети ремонтных подстанций, которые будут располагаться в некоторых населённых пунктах области и обслуживать другие близлежащие населённые пункты.

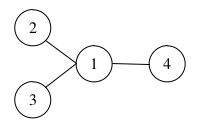
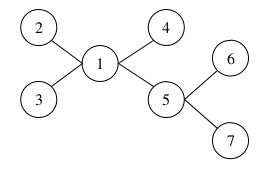
Система дорог в области устроена следующим простым образом. Есть $N$ населённых пунктов, некоторые из которых соединены дорогами. Между каждой парой пунктов существует не более одной дороги, и более того, для каждой пары населённых пунктов есть ровно один способ добраться из одного в другой (возможно, через промежуточные посёлки).

В каждом населённом пункте можно разместить ремонтную подстанцию. В принципе, фирма может размещать как крупные подстанции, которые даже в одиночку смогут обслуживать всю область, но при этом будут требовать больших расходов на содержание, так и небольшие станции, которые будут обслуживать лишь прилегающие населённые пункты, но при этом будут обходиться намного дешевле. Фирма уже определила, что каждую подстанцию можно характеризовать параметром “мощность”, которая может принимать значения, являющиеся целыми положительными числами (равна нулю мощность быть не может). Подстанция с мощностью $k$ будет обслуживать населённый пункт u, в котором она расположена, и все другие населённые пункты, до которых можно добраться из u, использовав не более k дорог (т.е. при $k$=1, например, подстанция обслуживает свой населённый пункт и все, которые напрямую соединены с ним дорогой). Стоимость содержания такой подстанции пропорциональна её мощности.

Теперь перед руководством фирмы и, в частности, вашим другом, стоит задача придумать схему расположения подстанций в населённых пунктах области так, чтобы, во-первых, каждый населённый пункт обслуживался хотя бы одной подстанцией, а во-вторых, суммарная мощность созданных подстанций была минимальна.

Как показывает статистика, автобусы намного реже ломаются на дорогах, чем внутри населённых пунктов, где они вынуждены часто изменять скорость, останавливаться, трогаться с места, заводить двигатель и т.д., поэтому не важно, все ли дороги обслуживаются — главное, чтобы обслуживались все населённые пункты.

Входные данные

В первой строке входного файла находится одно число $N$ — количество населённых пунктов в области (1<=$N$<=300). Далее следуют $N$−1 строка, описывающая дороги. Каждая строка содержит два числа — номера населённых пунктов, которые соединяет эта дорога. Населённые пункты нумеруются от 1 до $N$.

Выходные данные

В первую строку выходного файла выведите одно число — оптимальную суммарную мощность подстанций. Далее выведите $N$ чисел, описывающих какое-нибудь оптимальное решение. $i$-ое из этих чисел должно быть равно мощности подстанции, которую в вашем решении надо расположить в пункте $i$, или 0, если в населённом пункте $i$ не должна находиться подстанция.

Примеры

Входные данные

Выходные данные

1
1 0 0 0 0

Страница: 1 Отображать по:

Выбрано

Отменить

Добавить в контест