Страница: 1 2 3 >> Отображать по:
#600
Цепочка слов
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Будем называть цепочкой слов длины n последовательность слов \(w_1\), \(w_2\), …, \(w_n\), такую, что для всех \(i\) от 1 до \(n\) – 1 слово \(w_i\) является собственным префиксом слова \(w_i\)+1.

Слово \(u\) длины \(k\) называется собственным префиксом слова \(v\) длины \(l\), если \(l\) > \(k\) и первые \(k\) букв слова \(v\) совпадают со словом \(u\). Например, «program» является собственным префиксом слова «programmer».

Задано множество слов \(S\) = {\(s_1\), \(s_2\), …, \(s_m\)} и последовательность чисел \(x\)[1], \(x\)[2], …, \(x\)[\(k\)]. Требуется найти такие числа \(l\) и \(r\) (\(l\) ≤ \(r\)), что \(s_x\)[\(l\)], \(s_x\)[\(l\) + 1], …, \(s_x\)[\(r\) – 1], \(s_x\)[\(r\)] является цепочкой слов, и количество слов в цепочке (число \(r\) – \(l\) + 1) максимально.

Входные данные

Первая строка входного файла содержит целое число \(m\) (1 ≤ \(m\) ≤ 250 000). Каждая из следующих \(m\) строк содержит по одному слову из множества \(S\).

Все слова не пусты, имеют длину, не превосходящую 250 000 символов, и состоят только из строчных букв латинского алфавита. Суммарная длина всех слов не превосходит 250 000.

Следующая строка содержит число \(k\) (1 ≤ \(k\) ≤ 250 000). Последняя строка входного файла содержит \(k\) чисел — последовательность чисел \(x\)[1], \(x\)[2], …, \(x\)[\(k\)] (для всех \(i\) выполнено 1 ≤ \(x\)[\(i\)] ≤ \(m\)).

Выходные данные

Выведите в первой строке выходного файла два числа: \(l\) и \(r\). Если оптимальных ответов несколько, выведите любой из них. Разделяйте числа пробелом.

Примеры
Входные данные
3
zngs
rjzr
zng
3
3 1 1
Выходные данные
1 2
Входные данные
6
gjnuitvaowpy
gjnuitvaowpym
gjnuitvaowp
rjzrociinzeco
tgbotnzepnvm
aigqbzpnerv
9
2 3 1 2 3 1 2 3 1
Выходные данные
2 4
#1390
Симпатичные прямоугольники
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Знаменитый художник Вася только что закончил работу над своим новым шедевром и хочет знать, сколько он сможет получить за свой труд.

Картина представляет собой прямоугольник N на M сантиметров, разделенный на маленькие квадратики 1 на 1 сантиметр со сторонами, параллельными сторонам картины. Для достижения гармонии каждый из этих квадратиков Вася покрасил одним из 26 особых цветов, обозначаемых маленькими латинскими буквами.

Стоимость картины в точности равна количеству «симпатичных» частей в ней. Частью картины называется любой прямоугольник, который может быть вырезан из нее по границам квадратиков. Часть называется «симпатичной», если при выполнении симметрии относительно ее центра получается прямоугольник, раскрашенный также, как и исходная часть. Например, в картине, раскрашенной так:

abc
acb

симпатичными являются все части, состоящие из одного квадратика (их 6), а также части

bc и a

cb и a

Напишите программу, которая по информации о шедевре Васи определит его стоимость.

Входные данные

В первой строке содержатся два числа N и M (1 ≤ N, M ≤ 100). В следующих N строках идут строки, состоящие из M маленьких латинских символов. Символ в i-й строке j-м столбце определяет цвет соответствующего квадратика картины.

Выходные данные

Выведите стоимость шедевра — количество частей, симметричных относительно своего центра.

Комментарии к примерам тестов

Этот пример разобран в условии

Симпатичными являются шесть частей 1x1, одна часть 1x2 и сама картина.

Частичные ограничения

Первая группа состоит из тестов, в которых N, M ≤ 15. Данная группа оценивается в 30 баллов.

Вторая группа состоит из тестов, в которых N, M ≤ 50. Данная группа оценивается в 30 баллов.

Примеры
Входные данные
2 3
abc
acb
Выходные данные
8
Входные данные
3 2
ab
cc
ba
Выходные данные
8
#1750
Подпалиндромы
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Строка называется палиндромом, если она читается одинаково как слева направо, так и справа налево. Например, строки abba, ata являются палиндромами.

Дана строчка. Ее подстрокой называется некоторая непустая последовательность подряд идущих символов. Напишите программу, которая определит, сколько подстрок данной строки является палиндромами.

Входные данные

Вводится одна строка, состоящая из маленьких латинских букв. Длина строки не превышает 100000 символов.

Выходные данные

Выведите одно число — количество подстрок данной строки, являющихся палиндромами

Примеры
Входные данные
aaa
Выходные данные
6
Входные данные
aba
Выходные данные
4
#3395
Снова в космос
  
Темы: [Хеш]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

К 50-летию первого пилотируемого полета в космос решено создать новый тип космического корабля многоразового использования “Восторг”. Прямоугольная часть его корпуса (далее прямоугольник) должна быть облицована квадратными термозащитными плитками разных цветов одного и того же размера. Прямоугольник состоит из \(r\) рядов по \(c\) плиток в каждом. Плитки должны образовывать заданный рисунок.

Облицовка космического корабля отдельными плитками очень трудоемка, поэтому для выкладывания заданного рисунка используются одинаковые прямоугольные панели, состоящие из плиток. Панели крепятся на корпусе одна за другой, заполняя ряд за рядом сверху вниз. Каждый ряд панелей может быть сдвинут относительно предыдущего на одно и то же число плиток. При этом панели могут выходить за пределы прямоугольника. Панели должны быть одинаково ориентированы, то есть при параллельном переносе одной панели на место другой цвета образующих эти панели плиток должны совпадать.

Главный конструктор хочет выбрать такой размер панели \(a\times b\) и сдвиг \(s\), чтобы этими панелями можно было выложить заданный рисунок, и площадь панели была минимальна.


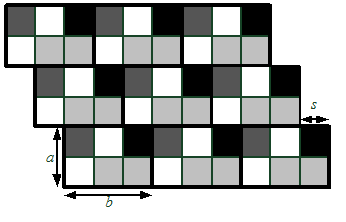
Пример панелей с \(a = 2\), \(b = 3\), \(s = 1\).

Требуется написать программу, которая по заданному расположению плиток в прямоугольнике рассчитывает размеры минимальной по площади панели, которую можно использовать при его облицовке, а также величину сдвига вправо (\(0 \leq s < b\)) каждого следующего ряда относительно предыдущего.

Входные данные

Первая строка входного файла содержит два целых числа: \(r\) и \(c\) – размеры прямоугольника в плитках. В последующих \(r\) строках указаны цвета плиток фрагмента. Каждый из \(k \leq 26\) цветов обозначен одной из первых \(k\) прописных букв латинского алфавита. Гарантируется, что для этого прямоугольника можно подобрать панель размера \(a\times b\), такую, что \(2a \leq r\) и \(2b \leq c\).

Выходные данные

ВВ выходной файл необходимо вывести три целых числа \(a\), \(b\) и \(s\), удовлетворяющих условиям задачи. Если решений несколько, разрешается вывести любое из них.

Комментарий

Во втором примере облицовка прямоугольника соответствуют следующему рисунку (выступающие за границы прямоугольника части панелей не показаны):

Подзадачи и система оценки

Данная задача содержит семь подзадач. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

Подзадача 1 (10 баллов)

В правильном ответе величина сдвига \(s\) равна нулю, \(r\) и \(c\) не превосходят 20.

Подзадача 2 (15 баллов)

В правильном ответе величина сдвига \(s\) равна нулю, \(r\) и \(c\) не превосходят 200.

Подзадача 3 (20 баллов)

В правильном ответе величина сдвига \(s\) равна нулю, \(r\) и \(c\) не превосходят 1961.

Подзадача 4 (10 баллов)

Величина сдвига \(s\) произвольна, \(r\) и \(c\) не превосходят 20.

Подзадача 5 (15 баллов)

Величина сдвига \(s\) произвольна, \(r\) и \(c\) не превосходят 200.

Подзадача 6 (15 баллов)

Величина сдвига \(s\) произвольна, \(r\) и \(c\) не превосходят 500.

Подзадача 7 (15 баллов)

Величина сдвига \(s\) произвольна, \(r\) и \(c\) не превосходят 1961.

Примеры
Входные данные
2 4
ABAB
ABAB
Выходные данные
1 2 0
Входные данные
5 7
DCADCAD
BABBABB
ADCADCA
BBABBAB
CADCADC
Выходные данные
2 3 1
#3871
«Abracadabra»
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Строка s называется супрефиксом для строки t, если t начинается с s и заканчивается на s. Например, «abra» является супрефиксом для строки «abracadabra». В частности, сама строка t является своим супрефиксом. Супрефиксы играют важную роль в различных алгоритмах на строках.

В этой задаче требуется решить обратную задачу о поиске супрефикса, которая заключается в следующем. Задан словарь, содержащий n слов t1, t2, …, tn и набор из m строк-образцов s1, s2, …, sm. Необходимо для каждой строки-образца из заданного набора найти количество слов в словаре, для которых эта строка-образец является супрефиксом.

Требуется написать программу, которая по заданному числу n, n словам словаря t1, t2, …, tn, заданному числу m и m строкам-образцам s1, s2, …, sm вычислит для каждой строки-образца количество слов из словаря, для которых эта строка-образец является супрефиксом.

Входные данные

Первая строка входного файла содержит целое число n (1 ≤ n ≤ 200 000).

Последующие n строк содержат слова t1, t2, …, tn, по одному слову в каждой строке. Каждое слово состоит из строчных букв латинского алфавита. Длина каждого слова не превышает 50. Суммарная длина всех слов не превышает 106. Словарь не содержит пустых слов.

Затем следует строка, содержащая целое число m (1 ≤ m ≤ 200 000).

Последующие m строк содержат строки-образцы s1, s2, …, sm, по одной на каждой строке. Каждая строка-образец состоит из строчных букв латинского алфавита: Длина каждой строки-образца не превышает 50. Суммарная длина всех строк-образцов не превышает 106. Никакая строка-образец не является пустой строкой.

Выходные данные

Выходной файл должен содержать m чисел, по одному на строке.

Для каждой строки-образца в порядке, в котором они заданы во входном файле, следует вывести количество слов словаря, для которых она является супрефиксом.

Система оценки

Решения, работающие при \(n\), \(m\) не превосходящими 100 оцениваются из 30 баллов.

Примеры
Входные данные
4
abacaba
abracadabra
aa
abra
3
a
abra
abac
Выходные данные
4
2
0
Страница: 1 2 3 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест