Страница: 1 Отображать по:

#600

Цепочка слов

Темы: ["Два указателя"] [Хеш]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Окружная олимпиада, 2007, 1 тур, Задача C ]

Будем называть цепочкой слов длины n последовательность слов \(w_1\), \(w_2\), …, \(w_n\), такую, что для всех \(i\) от 1 до \(n\) – 1 слово \(w_i\) является собственным префиксом слова \(w_i\)+1.

Слово \(u\) длины \(k\) называется собственным префиксом слова \(v\) длины \(l\), если \(l\) > \(k\) и первые \(k\) букв слова \(v\) совпадают со словом \(u\). Например, «program» является собственным префиксом слова «programmer».

Задано множество слов \(S\) = {\(s_1\), \(s_2\), …, \(s_m\)} и последовательность чисел \(x\)[1], \(x\)[2], …, \(x\)[\(k\)]. Требуется найти такие числа \(l\) и \(r\) (\(l\) ≤ \(r\)), что \(s_x\)[\(l\)], \(s_x\)[\(l\) + 1], …, \(s_x\)[\(r\) – 1], \(s_x\)[\(r\)] является цепочкой слов, и количество слов в цепочке (число \(r\) – \(l\) + 1) максимально.

Входные данные

Первая строка входного файла содержит целое число \(m\) (1 ≤ \(m\) ≤ 250 000). Каждая из следующих \(m\) строк содержит по одному слову из множества \(S\).

Все слова не пусты, имеют длину, не превосходящую 250 000 символов, и состоят только из строчных букв латинского алфавита. Суммарная длина всех слов не превосходит 250 000.

Следующая строка содержит число \(k\) (1 ≤ \(k\) ≤ 250 000). Последняя строка входного файла содержит \(k\) чисел — последовательность чисел \(x\)[1], \(x\)[2], …, \(x\)[\(k\)] (для всех \(i\) выполнено 1 ≤ \(x\)[\(i\)] ≤ \(m\)).

Выходные данные

Выведите в первой строке выходного файла два числа: \(l\) и \(r\). Если оптимальных ответов несколько, выведите любой из них. Разделяйте числа пробелом.

Примеры

Входные данные

3
zngs
rjzr
zng
3
3 1 1

Выходные данные

1 2

Входные данные

6
gjnuitvaowpy
gjnuitvaowpym
gjnuitvaowp
rjzrociinzeco
tgbotnzepnvm
aigqbzpnerv
9
2 3 1 2 3 1 2 3 1

Выходные данные

2 4

#3395

Снова в космос

Темы: [Хеш]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2011, Задача C ]

К 50-летию первого пилотируемого полета в космос решено создать новый тип космического корабля многоразового использования “Восторг”. Прямоугольная часть его корпуса (далее прямоугольник) должна быть облицована квадратными термозащитными плитками разных цветов одного и того же размера. Прямоугольник состоит из \(r\) рядов по \(c\) плиток в каждом. Плитки должны образовывать заданный рисунок.

Облицовка космического корабля отдельными плитками очень трудоемка, поэтому для выкладывания заданного рисунка используются одинаковые прямоугольные панели, состоящие из плиток. Панели крепятся на корпусе одна за другой, заполняя ряд за рядом сверху вниз. Каждый ряд панелей может быть сдвинут относительно предыдущего на одно и то же число плиток. При этом панели могут выходить за пределы прямоугольника. Панели должны быть одинаково ориентированы, то есть при параллельном переносе одной панели на место другой цвета образующих эти панели плиток должны совпадать.

Главный конструктор хочет выбрать такой размер панели \(a\times b\) и сдвиг \(s\), чтобы этими панелями можно было выложить заданный рисунок, и площадь панели была минимальна.

Пример панелей с \(a = 2\), \(b = 3\), \(s = 1\).

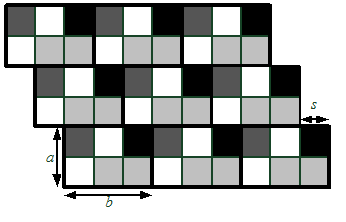
Требуется написать программу, которая по заданному расположению плиток в прямоугольнике рассчитывает размеры минимальной по площади панели, которую можно использовать при его облицовке, а также величину сдвига вправо (\(0 \leq s < b\)) каждого следующего ряда относительно предыдущего.

Входные данные

Первая строка входного файла содержит два целых числа: \(r\) и \(c\) – размеры прямоугольника в плитках. В последующих \(r\) строках указаны цвета плиток фрагмента. Каждый из \(k \leq 26\) цветов обозначен одной из первых \(k\) прописных букв латинского алфавита. Гарантируется, что для этого прямоугольника можно подобрать панель размера \(a\times b\), такую, что \(2a \leq r\) и \(2b \leq c\).

Выходные данные

ВВ выходной файл необходимо вывести три целых числа \(a\), \(b\) и \(s\), удовлетворяющих условиям задачи. Если решений несколько, разрешается вывести любое из них.

Комментарий

Во втором примере облицовка прямоугольника соответствуют следующему рисунку (выступающие за границы прямоугольника части панелей не показаны):

Подзадачи и система оценки

Данная задача содержит семь подзадач. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

Подзадача 1 (10 баллов)

В правильном ответе величина сдвига \(s\) равна нулю, \(r\) и \(c\) не превосходят 20.

Подзадача 2 (15 баллов)

В правильном ответе величина сдвига \(s\) равна нулю, \(r\) и \(c\) не превосходят 200.

Подзадача 3 (20 баллов)

В правильном ответе величина сдвига \(s\) равна нулю, \(r\) и \(c\) не превосходят 1961.

Подзадача 4 (10 баллов)

Величина сдвига \(s\) произвольна, \(r\) и \(c\) не превосходят 20.

Подзадача 5 (15 баллов)

Величина сдвига \(s\) произвольна, \(r\) и \(c\) не превосходят 200.

Подзадача 6 (15 баллов)

Величина сдвига \(s\) произвольна, \(r\) и \(c\) не превосходят 500.

Подзадача 7 (15 баллов)

Величина сдвига \(s\) произвольна, \(r\) и \(c\) не превосходят 1961.

Примеры

Входные данные

2 4
ABAB
ABAB

Выходные данные

1 2 0

Входные данные

5 7
DCADCAD
BABBABB
ADCADCA
BBABBAB
CADCADC

Выходные данные

2 3 1

#3871

«Abracadabra»

Темы: [Хеш] [Бор] [Бинарный поиск в массиве] [Строки]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2012, 2 день, Задача D ]

Строка s называется супрефиксом для строки t, если t начинается с s и заканчивается на s. Например, «abra» является супрефиксом для строки «abracadabra». В частности, сама строка t является своим супрефиксом. Супрефиксы играют важную роль в различных алгоритмах на строках.

В этой задаче требуется решить обратную задачу о поиске супрефикса, которая заключается в следующем. Задан словарь, содержащий n слов t₁, t₂, …, t_n и набор из m строк-образцов s₁, s₂, …, s_m. Необходимо для каждой строки-образца из заданного набора найти количество слов в словаре, для которых эта строка-образец является супрефиксом.

Требуется написать программу, которая по заданному числу n, n словам словаря t₁, t₂, …, t_n, заданному числу m и m строкам-образцам s₁, s₂, …, s_m вычислит для каждой строки-образца количество слов из словаря, для которых эта строка-образец является супрефиксом.

Входные данные

Первая строка входного файла содержит целое число n (1 ≤ n ≤ 200 000).

Последующие n строк содержат слова t₁, t₂, …, t_n_, по одному слову в каждой строке. Каждое слово состоит из строчных букв латинского алфавита. Длина каждого слова не превышает 50. Суммарная длина всех слов не превышает 10⁶. Словарь не содержит пустых слов.

Затем следует строка, содержащая целое число m (1 ≤ m ≤ 200 000).

Последующие m строк содержат строки-образцы s₁, s₂, …, s_m, по одной на каждой строке. Каждая строка-образец состоит из строчных букв латинского алфавита: Длина каждой строки-образца не превышает 50. Суммарная длина всех строк-образцов не превышает 10⁶. Никакая строка-образец не является пустой строкой.

Выходные данные

Выходной файл должен содержать m чисел, по одному на строке.

Для каждой строки-образца в порядке, в котором они заданы во входном файле, следует вывести количество слов словаря, для которых она является супрефиксом.

Система оценки

Решения, работающие при \(n\), \(m\) не превосходящими 100 оцениваются из 30 баллов.

Примеры

Входные данные

4
abacaba
abracadabra
aa
abra
3
a
abra
abac

Выходные данные

4
2
0

#111226

Театр начинается с актеров

Темы: [Хеш]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2012, Задача F ]

Участники олимпиады пришли в казанский театр на спектакль, где играют N неизвестных для них актеров. В фойе театра висят портреты всех актеров труппы, которая в полном составе задействована в спектакле. Портреты не подписаны. Зрителям раздали программки, в которых для каждого действия спектакля приводится список фамилий участвующих в нем актеров, но не указаны их роли. Театрал Виталий решил узнать, как выглядит каждый из актеров, упомянутых в программке. Для этого в антракте после каждого действия он выходил в фойе и сопоставлял портреты с увиденными актерами. Требуется написать программу, которая по заданному числу актеров N и списку фамилий актеров, участвующих в каждом из M действий, определяет номер действия, после которого впервые становится возможным установить соответствие между фамилией актера из программки и его портретом.

Входные данные

Первая строка входного файла содержит два натуральных числа N – число актеров и M – количество действий в спектакле (1 < N ≤ 100000, 1 ≤ M ≤ 100 000). В каждой из следующих M строк сначала записано количество актеров K_i, участвующих в i–ом действии (1 ≤ K_i ≤ N, K₁ + K₂ + ... + K_M ≤ 100 000), а затем K_i различных натуральных чисел, не превосходящих N, обозначающих фамилии этих актеров. Соседние числа в каждой строке разделены пробелом.

Выходные данные

Выходной файл должен содержать одну строку, состоящую из N записанных через пробел чисел. i-е число этой строки – это номер действия, после которого впервые становится возможным установить соответствие между i–м актером и его портретом. Если к концу спектакля установить соответствие между каким-либо актером и его портретом так и не удалось, то соответствующее число в строке должно быть равно нулю.

Примечание

В первом примере три актера участвуют в спектакле с тремя действиями. В первом действии участвуют два актера с номерами 1 и 2. Так как актеров всего трое, то после первого акта становится понятно, какой портрет соответствует актеру с номером 3, поэтому третье число строки выходного файла равно 1. Во втором действии участвуют два актера с номерами 3 и 2. Поскольку только второй актер участвовал и в первом, и во втором действиях, то его портрет можно определить после второго действия. А так как портретов всего три, то после второго действия можно установить, что последний портрет соответствует актеру номер 1. Третье действие на ответ не влияет.

Данная задача содержит три подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

(оценивается в 30 баллов) Количество актеров N не превосходит 100, количество действий M не превосходит 100, K₁ + K₂ + ... + K_M ≤ 100.
(оценивается в 30 баллов) Количество актеров N не превосходит 10 000, количество действий M не превосходит 10 000, K₁ + K₂ + ... + K_M ≤ 10 000.
(оценивается в 40 баллов) Количество актеров N не превосходит 100 000, количество действий M не превосходит 100 000, K₁ + K₂ + ... + K_M ≤ 100 000.

Примеры

Входные данные

Выходные данные

2 2 1

Входные данные

Выходные данные

0 3 0 0 0

Входные данные

Выходные данные

1 3 2 3

Страница: 1 Отображать по:

Выбрано

Отменить

Добавить в контест