Турнир Архимеда(52 задач)
Кировские командные турниры(8 задач)
Барнаульские командные турниры(10 задач)
Московская командная олимпиада(246 задач)
Командные чемпионаты школьников Санкт-Петербурга по программированию(167 задач)
ВКОШП(180 задач)
В одном феодальном государстве средневековой Европы было n городов и m дорог, каждая из которых соединяла некоторые два города. Каждая дорога принадлежала правителю одного из городов (не обязательно одного из тех, которые она соединяла). Однажды правитель города S решил объявить войну правителю города T. Перед ним сразу же встала нелегкая задача: как довести армию до города T.
Правитель каждого города требует плату за проход войск через его город. Кроме того, правитель города S может перемещать войска только по дорогам, которые принадлежат ему. При этом он может купить любую дорогу у ее владельца за определенную плату (даже если владелец – правитель города T). К сожалению, все деньги из казны города S были потрачены на предыдущий неудачный военный поход, поэтому сначала правителю придется продать некоторые свои дороги (разумеется, после этого он не сможет провести по ним войска).
Помогите правителю выяснить, какие дороги следует продать, а какие купить, чтобы довести войска от города S до города T и оплатить проход через все промежуточные города. Все операции продажи и покупки дорог надо осуществить до начала похода, пока правители других городов не догадались о воинственных намерениях правителя города S.
В первой строке вводятся целые числа n и m – количество городов и дорог соответственно ( 2![]() n
n![]() 2 000, 1
2 000, 1![]() m
m![]() 50 000). Города нумеруются от 1 до n, города S и T имеют номера 1 и n соответственно.
50 000). Города нумеруются от 1 до n, города S и T имеют номера 1 и n соответственно.
Следующие n строк содержат под одному целому числу ri – плату за проезд через город i ( 0![]() ri
ri![]() 10 000, r1 = rn = 0).
10 000, r1 = rn = 0).
Далее идут m строк, задающих описания дорог. Дорога описывается четырьмя целыми числами: ai, bi, pi и ci. Здесь ai и bi – номера городов, которые соединяет дорога, pi – номер города, правителю которого она принадлежит, ci – ее стоимость ( ai![]() bi, 1
bi, 1![]() ci
ci![]() 10 000). По дороге можно перемещаться в обоих направлениях. Любые два города соединены не более, чем одной дорогой.
10 000). По дороге можно перемещаться в обоих направлениях. Любые два города соединены не более, чем одной дорогой.
В первой строке выведите список дорог, которые нужно продать в следующем формате: сначала число дорог, а затем их номера. Дороги нумеруются с единицы в том порядке, в котором они заданы во входных данных. Во второй строке выведите список дорог, которые нужно купить, в том же формате. В третьей строке выведите маршрут похода – номера городов в порядке следования войска. Если решений несколько, выведите любое.
Если решения нет, выведите число -1.
3 3 0 1 0 1 2 1 10 2 3 1 10 3 1 2 2
2 1 2 1 3 1 3
Максимальное время работы на одном тесте: 2 секунды
Телевидение Флатландии готовится показать в вечернем эфире выступление одного известного политика. Поскольку политик известен своей несдержанностью, решено было написать специальную программу, которая вырезала бы из речи политика некоторые фразы, запуская в этот момент рекламу.
Поскольку ввести все неполиткорректные слова в программу представляется довольно сложным, решено было использовать эвристический алгоритм определения адекватности фразы.
Речь политика в реальном времени оцифровывается, распознается и подается на вход программе как последовательность фраз. Каждая фраза состоит из слов, записанных в одну строку. Слово представляет собой последовательность символов, ограниченную с обеих сторон границами фразы, пробелами или знаками препинания (символами «.», «!», «?», «:», «-», «,», «;», «(» или «)»).
Слово считается подозрительным, если в него входит не более трех различных букв (любой символ, кроме пробелов и знаков препинания считается буквой, большие и маленькие буквы считаются различными). Например, слова «дом», «мама» или «шалаш» являются подозрительными, а слова «привет», «Шалаш» или «hello» – нет.
Фраза считается подозрительной, если не менее половины слов в ней подозрительны (каждое вхождение слова во фразу считается отдельно).
Напишите программу, которая процензурирует речь политика, удалив из нее все подозрительные фразы.
Формат входных данных
Вводится не более 1000 фраз, каждая из которых представляет собой строку не длиннее 250 символов. Фраза содержит только символы с ASCII кодами от 32 до 255.
Формат выходных данных
Выведите все фразы из входных данных, которые не являются подозрительными. Фразы следует выводить в том же порядке, в котором они поступали на вход программы.
Примеры
| Входные данные | Выходные данные |
Наша система власти достаточно стабильна. | Наша система власти достаточно стабильна. |
Ваня очень любит шахматы. Причем он не только любит просто играть в шахматы, но часто придумывает разные головоломки и просто забавные задачки с использованием шахматных фигур. Также вместо стандартной шахматной доски 8×8 Ваня часто использует в своих задачах доски другого размера.
Недавно он придумал новую головоломку и рассказал ее своим друзьям. Суть головоломки заключается в следующем. На одно из полей доски размером m×n записывается некоторое положительное целое число и затем на него ставится ферзь.
После этого Ваня делает k ходов ферзем, каждый раз перемещая его по шахматным правилам на одно из полей, на котором он еще не был. При этом каждый раз, перед тем как поставить ферзя на некоторое поле, он записывает на это поле целое число, причем это число всегда больше всех чисел, уже записанных на доске.
Задача друзей Вани – по числам, записанным на доске, восстановить маршрут ферзя или выяснить, что Ваня где-то ошибся. Поскольку Ваня часто выбирает достаточно большие m, n и k, друзья устали решать эту головоломку вручную и решили написать для ее решения программу. Помогите им
Напомним, что по шахматным правилам ферзь может пойти на любое поле доски, находящееся на одной вертикали, горизонтали или диагонали с тем полем, на котором он находится.
В первой строке вводятся числа m, n и k ( 1![]() m, n
m, n![]() 300, 0
300, 0![]() k < mn). Следующие m строк содержат по n целых чисел и описывают поля доски (пустому полю соответствует число 0, а полю, на котором записано число – это число). Все числа, записанные на доске, положительные, целые и не превышают 109.
k < mn). Следующие m строк содержат по n целых чисел и описывают поля доски (пустому полю соответствует число 0, а полю, на котором записано число – это число). Все числа, записанные на доске, положительные, целые и не превышают 109.
Если Ваня ошибся при построении головоломки, выведите сообщение «Wrong Board».
В противном случае выведите m строк по n чисел – для каждого поля выведите номер хода, перед которым ферзь побывал на этом поле, а для последнего поля, на котором он оказался – число k + 1. Для полей, на которые ферзь не попадал, выведите число 0.
4 4 7 10 20 0 100 30 0 0 40 0 0 0 0 45 42 0 70
1 2 0 8 3 0 0 4 0 0 0 0 6 5 0 7
2 4 4 10 20 30 40 0 50 0 0
Wrong Board
2 2 2 1 2 4 3
Wrong Board
Год назад Флатландию потряс серьезный экономический кризис, после которого, с целью снижения издержек, фермер Джон и фермер Билл решили объединить свои фермы. За год совместной продуктивной работы на объединенной территории было построено четыре сарая.
Однако последствия кризиса в последнее время ощущаются все меньше, да и совместное ведение хозяйства – дело непростое. Поэтому фермеры решили снова разделить свои фермы.
Для раздела ферм решено было построить забор. Разумеется, прежде чем приступить к строительству, фермеры взяли карту совместного хозяйства и стали обсуждать возможное положение забора. Забор должен представлять собой прямую линию. Поскольку по закону границы участков должны быть направлены либо с севера на юг, либо с запада на восток, забор на карте должен представлять собой прямую, параллельную краю карты – вертикальную либо горизонтальную.
Единственная проблема – четыре построенных за год совместной работы сарая. Разумеется, каждому фермеру в результате раздела должно достаться по два сарая. Поэтому после постройки забора два сарая должны оказаться с одной стороны от него, а два других – с другой.
Помогите фермерам найти такое положение для забора. Забор может проходить непосредственно вдоль стены сарая.
На вход программы поступают четыре четверки целых чисел. Каждая четверка описывает один сарай. Первые два числа в описании сарая – это координаты на карте его левого нижнего угла, следующие два числа – координаты правого верхнего угла.
Система координат размещена таким образом, что ось OX направлена слева направо, а ось OY – снизу вверх. Оси координат параллельны краям карты. Стороны сараев также параллельны краям карты. Сараи не имеют общих точек. Каждый сарай имеет ненулевую площадь. Все координаты неотрицательны и не превышают 109.
Если построить забор, удовлетворяющий всем условиям, невозможно, выведите слово «Impossible».
В противном случае в первой строке выведите слово «Vertical», если забор следует построить параллельно вертикальному краю карты, или слово «Horizontal», если забор следует построить параллельно горизонтальному краю карты.
В следующей строке выведите координату x всех точек забора, если он должен быть вертикальным, либо координату y всех точек забора, если он должен быть горизонтальным. Выведенная координата должна быть целым числом (несложно показать, что если забор можно построить, то его можно построить так, чтобы искомая координата была целой).
Приведенные ниже рисунки соответствуют примерам входных данных.
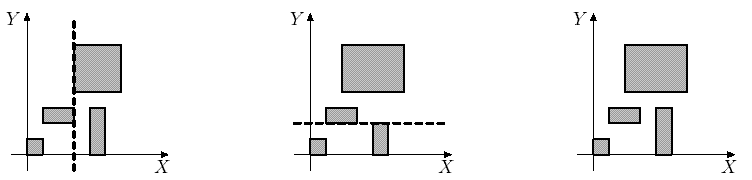
0 0 1 1 1 2 3 3 4 0 5 3 3 4 6 7
Vertical 3
0 0 1 1 1 2 3 3 4 0 5 2 2 4 6 7
Horizontal 2
0 0 1 1 1 2 3 3 4 0 5 3 2 4 6 7
Impossible
Сережа очень любит старые игры. Недавно он нашел у себя на компьютере одну старую приключенческую игру. Управляя героем, надо перемещаться по карте и собирать различные предметы.
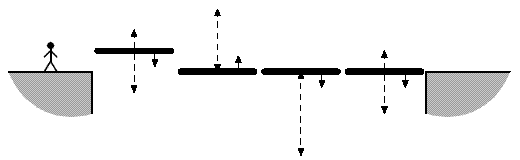
На определенном этапе игры Сережа столкнулся с неожиданной проблемой. Для продолжения приключений герою надо перебраться через пропасть. Для этого можно использовать последовательно расположенные лифты, которые имеют вид горизонтальных платформ. Каждый лифт вертикально перемещается туда-сюда между некоторыми уровнями. Герой может переходить между соседними платформами, однако это можно сделать только в тот момент, когда они находятся на одном уровне. Аналогично, с края пропасти на лифт и обратно можно перейти лишь в тот момент, когда лифт окажется на уровне края.
Каждый лифт имеет ширину, равную четырем метрам. В начале герой находится на расстоянии два метра от края пропасти. Он должен закончить свое путешествие в двух метрах от противоположного края пропасти. Герой перемещается со скоростью два метра в секунду. Таким образом, если герой находится в начальном положении или в центре лифта и хочет перейти на соседний лифт (или сойти с последнего лифта на противоположный край пропасти), он должен начать движение ровно за одну секунду до того момента, когда они окажутся на одном уровне. Через две секунды герой оказывается в центре соседнего лифта (или в конечном положении).
Края пропасти находятся на одном уровне. Для каждого лифта задан диапазон высот, между которыми он перемещается, начальное положение и направление движения в начальный момент. Все лифты перемещаются со скоростью один метр в секундy. Выясните, сможет ли герой перебраться на противоположный край пропасти, и если да, то какое минимальное время ему для этого понадобится.
В первой строке вводится целое число n – количество лифтов ( 1![]() n
n![]() 100). Следующие n строк содержат описания лифтов.
100). Следующие n строк содержат описания лифтов.
Каждое описание состоит из четырех целых чисел: l, u, s – самое нижнее, самое верхнее и начальное положение лифта относительно края пропасти в метрах ( -100![]() l
l![]() s
s![]() u
u![]() 100, l < u), и d – направление движения лифта в начальный момент (d = 1 означает, что лифт двигается вверх, d = - 1 – вниз).
100, l < u), и d – направление движения лифта в начальный момент (d = 1 означает, что лифт двигается вверх, d = - 1 – вниз).
Выведите минимальное время в секундах, необходимое для того, чтобы перебраться на противоположный край пропасти. Если перебраться на противоположный край пропасти невозможно, выведите число -1.
4 -1 2 1 -1 0 3 0 1 -4 0 0 -1 -2 1 0 -1
29