Страница: << 1 2 3 >> Отображать по:
#563
Парты
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Сколько понадобится парт, чтобы рассадить \(A\) школьников, если за одну парту можно посадить одного или двух человек? За каждой партой должен сидеть хотя бы один человек. Укажите все варианты.

Входные данные

Вводится одно натуральное число — \(A\) ( 1 ≤ \(A\) ≤ 10000)

Выходные данные

Выведите упорядоченный по возрастанию набор чисел – все возможные значения количества необходимых парт.

Примеры
Входные данные
6
Выходные данные
3 4 5 6
#773
Excel
  
Темы: [Цикл for]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

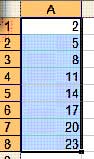Задача А, рис.1Если в Microsoft Excel выделить две соседние клетки с числами, а потом “потянуть” за правый нижний уголок мышью, то следующие клетки заполнятся числами, образуя арифметическую прогрессию.

Входные данные

Вводятся сначала два натуральных числа, по модулю не превышающие 100 – числа в первых двух клетках, а затем число N (натуральное, 2 ≤ N ≤ 100) – общее количество чисел в арифметической прогрессии (включая два первых числа). Числа вводятся через пробел. 

Выходные данные

Выведите N членов арифметической прогрессии, разделяя их пробелом.

Примеры
Входные данные
2 5 8
Выходные данные
2 5 8 11 14 17 20 23
#777
Шулер
  
Темы: [Цикл for]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Колоду карт раздают по кругу, по одной карте каждому за раз, пока колода не кончится. Известен порядок карт в колоде. С кого должен начинать сдающий, чтобы первый игрок получил себе как можно больше тузов?

Входные данные

В первой строке вводятся два числа: количество игроков и количество карт в колоде (оба числа натуральные и не превосходят 100, количество карт делится на количество игроков).

Во второй строке через пробел перечислены достоинства карт в том порядке, в котором они идут в колоде (6 – шестерка, 7 – семерка, 8 – восьмерка, 9 – девятка, 10 – десятка, 11 – валет, 12 – дама, 13 – король, 14 – туз). В колоде может быть произвольное число карт каждого достоинства.

Выходные данные

Выведите одно число – номер игрока, с которого следует начинать сдавать, чтобы первый игрок получил как можно больше тузов (игроки нумеруются числами 1, 2, 3, ...; сдача происходит по возрастанию номеров начиная с некоторого до последнего, и затем продолжается с первого). Если вариантов ответа несколько, выведите любой из них.

Примеры
Входные данные
5 10
9 9 9 14 8 7 11 6 14 6
Выходные данные
3
Входные данные
3 3
14 14 14
Выходные данные
1
#792
Число
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Вводится натуральное число. Требуется разделить запятыми тройки его цифр (считая справа).

Входные данные

Вводится одно натуральное число, не превышающее 10100.

Выходные данные

Вывести то же число, разделяя тройки цифр запятыми.

Примеры
Входные данные
1000
Выходные данные
1,000
Входные данные
12345678
Выходные данные
12,345,678
Входные данные
999
Выходные данные
999
#867
Заполните массив
  
Темы: [Цикл for]
Требуется заполнить массив числами от 2 до N+1 так, чтобы каждое из них делилось на индекс элемента (нумерация элементов с 1).

Требуется заполнить N элементов массива, пронумерованных числами от 1 до N (A[1]…A[N]), натуральными числами от 2 до N+1, использовав каждое число ровно один раз, так, чтобы значение каждого элемента массива делилось бы нацело на его номер (т.е. для каждого i A[i] делилось бы на i).

Напишите программу, которая для заданного N заполнит массив согласно описанному правилу.

Входные данные

Вводится одно натуральное число N (1≤N≤1000).

Выходные данные

Выведите заполненный массив. Если вариантов заполнения несколько, выведите любой из них. Если заполнить массив невозможно, выведите одно число 0.

Пример

Входные данные

Выходные данные

2

3 2
Страница: << 1 2 3 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест