 Если в Microsoft Excel выделить две соседние клетки с числами, а потом “потянуть” за правый нижний уголок мышью, то следующие клетки заполнятся числами, образуя арифметическую прогрессию.
Если в Microsoft Excel выделить две соседние клетки с числами, а потом “потянуть” за правый нижний уголок мышью, то следующие клетки заполнятся числами, образуя арифметическую прогрессию.
Вводятся сначала два натуральных числа, по модулю не превышающие 100 – числа в первых двух клетках, а затем число N (натуральное, 2 ≤ N ≤ 100) – общее количество чисел в арифметической прогрессии (включая два первых числа). Числа вводятся через пробел.
Выведите N членов арифметической прогрессии, разделяя их пробелом.
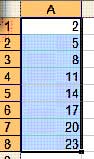
2 5 8
2 5 8 11 14 17 20 23
Шпион Коля зашифровал и послал в центр радиограмму. Он использовал такой способ шифровки: сначала выписал все символы своего сообщения (включая знаки препинания и т.п.), стоявшие на четных местах, в том же порядке, а затем – все символы, стоящие на нечетных местах. Напишите программу, которая расшифровывает сообщение.
Вводится одна непустая строка длиной не более 250 символов – зашифрованное сообщение. Строка может состоять из любых символов, кроме пробельных.
Выведите одну строку – расшифрованное сообщение.
rvt!Pie!
Privet!!
Какую наибольшую площадь может иметь прямоугольник периметра P, нарисованный на клетчатой бумаге по линиям сетки (сторона клетки равна 1)?
Вводится одно четное натуральное число P (4 ≤ P ≤ 600).
Выведите одно число – наибольшую возможную площадь.
4
1
6
2
Вы сидите на первом сидении в маршрутном такси. Проезд в маршрутке стоит 10 рублей. Вам передают купюры достоинством в 10, 50 и 100 рублей (с каждой купюры – на билет за одного пассажира). Часть из них вы можете сразу раздать в качестве сдачи (её можно выдать полностью или частично). Остальные купюры вы передаете водителю. Какое наименьшее количество купюр вам придется передать водителю?
Вводится три целых неотрицательных числа (каждое не превосходит 100) – количество 10-, 50- и 100-рублевых купюр, которые вам передали.
Выведите одно число – наименьшее возможное количество купюр, которое придется передать водителю.
1 1 1
1
9 0 2
2
Колоду карт раздают по кругу, по одной карте каждому за раз, пока колода не кончится. Известен порядок карт в колоде. С кого должен начинать сдающий, чтобы первый игрок получил себе как можно больше тузов?
В первой строке вводятся два числа: количество игроков и количество карт в колоде (оба числа натуральные и не превосходят 100, количество карт делится на количество игроков).
Во второй строке через пробел перечислены достоинства карт в том порядке, в котором они идут в колоде (6 – шестерка, 7 – семерка, 8 – восьмерка, 9 – девятка, 10 – десятка, 11 – валет, 12 – дама, 13 – король, 14 – туз). В колоде может быть произвольное число карт каждого достоинства.
Выведите одно число – номер игрока, с которого следует начинать сдавать, чтобы первый игрок получил как можно больше тузов (игроки нумеруются числами 1, 2, 3, ...; сдача происходит по возрастанию номеров начиная с некоторого до последнего, и затем продолжается с первого). Если вариантов ответа несколько, выведите любой из них.
5 10 9 9 9 14 8 7 11 6 14 6
3
3 3 14 14 14
1