Страница: << 1 2 3 4 5 >> Отображать по:
#423
В школу на велосипеде
  
Источники: [ Командные олимпиады, ВКОШП, 2004, Задача A ]
Даны две пересекающихся окружности. Необходимо найти кратчайший путь от точки до точки по окружностям.

Петя любит ездить в школу на велосипеде. Но ездить на велосипеде по тротуарам запрещено, а ездить по дороге опасно. Поэтому Петя ездит только по специальным велосипедным дорожкам. К счастью, и Петин дом, и Петина школа находятся в непосредственной близости от таких дорожек.

В городе, где живет Петя, есть ровно две велосипедных дорожки. Каждая дорожка имеет форму окружности. В точках их пересечения можно переехать с одной дорожки на другую.

Петя знает точку, в которой он заезжает на дорожку, и точку, в которой следует съехать, чтобы попасть в школу. Петю заинтересовал вопрос: какое минимальное расстояние ему следует проехать по дорожкам, чтобы попасть из дома в школу.

Входные данные

Будем считать, что в городе введена прямоугольная декартова система координат.

Первые две строки входных данных описывают велосипедные дорожки. Каждая из них содержит по три целых числа – координаты центра окружности, которую представляет собой соответствующая дорожка, и ее радиус. Координаты и радиус не превышают 200 по абсолютной величине, радиус – положительное число. Гарантируется, что дорожки не совпадают.

Следующие две строки содержат по два вещественных числа – координаты точки, где Петя заезжает на дорожку, и точки, в которой Петя съезжает с дорожки. Гарантируется, что каждая из точек с высокой точностью лежит на одной из дорожек (расстояние от точки до центра одной из окружностей отличается от ее радиуса не более, чем на 10-8). Точки могут лежать как на одной дорожке, так и на разных.

Выходные данные

Выведите  минимальное расстояние, которое следует проехать Пете по велосипедным дорожкам, чтобы попасть из дома в школу. Ответ должен отличаться от правильного не более, чем на 10-4.

Если доехать из дома до школы по велосипедным дорожкам невозможно, выведите  число -1.

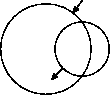
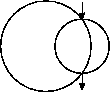
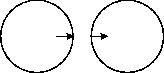
includegraphics{pics/bike.1} includegraphics{pics/bike.2} includegraphics{pics/bike.3}
Примеры
Входные данные
0 0 5
4 0 3
3.0 4.0
1.878679656440357 -2.121320343559643
Выходные данные
8.4875540166
Входные данные
0 0 5
4 0 3
4.0 3.0
4.0 -3.0
Выходные данные
6.4350110879
Входные данные
0 0 4
10 0 4
4.0 0.0
6.0 0.0
Выходные данные
-1
#519
Свет
  
Источники: [ Командные олимпиады, ВКОШП, 2003, Задача D ]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Дан точечный источник света и многоугольник. Необходимо пройти от заданной точки до ближайшей освещенной точки, не проходя через дом.

В точке (0, 0) координатной плоскости расположена лампочка, которая представляет собой точечный источник света. Неподалеку от лампочки находится дом Пети, который представляет собой выпуклый многоугольник с \(N\) вершинами. Сам Петя находится в точке с координатами (\(x\), \(y\)).

Петя хочет увидеть свет. Для этого ему необходимо оказаться в такое точке, что отрезок, соединяющей ее с началом координат, не пересекается с домом Пети (но может его касаться, в частности, проходить вдоль стороны многоугольника дома).

Петя может перемещаться по плоскости со скоростью \(v\). Разумеется, Петя не может проходить сквозь дом (хотя он может двигаться по его границе).

Выясните, какое минимальное время требуется Пете, чтобы оказаться в освещенной точке.

Входные данные

В первой строке вводятся координаты Пети – два неотрицательных вещественных числа, не превышающих 1000, и его скорость v – вещественное число, 10-2\( \le\) v\( \le\) \(10^4\).

Вторая строка содержит \(N\) – число вершин в многоугольнике, задающем Петин дом ( 3\( \le\)N\( \le\)100). Далее в \(N\) строках вводится по два вещественных числа – координаты вершин многоугольника в порядке их обхода против часовой стрелки. Все координаты неотрицательны и не превышают 1000.

Гарантируется, что входные данные корректны, в частности, многоугольник выпуклый, и никакие три его последовательные вершины не лежат на одной прямой. Также гарантируется, что и Петя, и лампочка находятся снаружи от многоугольника, в частности, не находятся на его границе. Расстояние от точки, где находится Петя, до многоугольника и от начала координат до многоугольника не меньше 10-2, расстояние от Пети до начала координат не меньше 10-2.

Выходные данные

Выведите минимальное время, за которое Петя сможет попасть в освещенную точку. Ваш ответ должен отличаться от правильного не более чем на 10-4.

Примеры
Входные данные
3.5 3.5 1.0
4
2.0 0.0
4.0 2.0
2.0 4.0
0.0 2.0
Выходные данные
3.58113883008418967000
#549
Триангуляция Делоне
  
Источники: [ Командные олимпиады, ВКОШП, 2001, Задача E ]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Требуется разбить данный многоугольник на треугольники с вершинами, совпадающими с вершинами многоугольников или находящимися внутри многоугольника, так, чтобы внутри окружностей, описанных вокруг треугольников не лежала ни одна вершина многоугольника.

Триангуляцией некоторого набора точек на плоскости называется набор невырожденных треугольников, удовлетворяющий следующим свойствам:

1) Вершинами треугольников являются только точки исходного набора. Каждая точка исходного набора является вершиной хотя бы одного треугольника.
2) Два различных треугольника либо не имеют общих точек, либо имеют общую вершину, либо имеют общую сторону (но площадь их пересечения всегда равна 0).
3) Любая точка, лежащая внутри выпуклой оболочки исходного набора точек, принадлежит хотя бы одному треугольнику (она может принадлежать нескольким треугольникам, если является их общей вершиной или принадлежит их общей стороне). (Выпуклой оболочкой некоторого набора точек называется наименьший выпуклый многоугольник, содержащий все эти точки).
Триангуляция называется триангуляцией Делоне, если кроме того для нее выполняется следующее условие:

Внутри окружности, описанной около любого треугольника из триангуляции, не лежит ни одна из исходных точек (точки могут лежать на окружности, в частности на ней, очевидно, лежат вершины рассматриваемого треугольника).

Для заданного набора точек найдите количество его триангуляций Делоне (две триангуляции считаются различными, если они отличаются хотя бы одним треугольником).

Входные данные

В первой строке вводится число \(N\) - количество точек (3 <= \(N\) <= 30) исходного набора. Следующие \(N\) строк содержат по одной паре вещественных чисел - координаты соответствующей точки. Никакие три точки не лежат на одной прямой.

Выходные данные

Выведите количество различных триангуляций Делоне указанного набора точек.

Примеры
Входные данные
4
0.0 0.0
1.0 0.0
0.0 1.0
1.0 1.0
Выходные данные
2
#585
Фонтан
  
Источники: [ Командные олимпиады, ВКОШП, 2000, Задача C ]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
В прямоугольном зале с круглыми колоннами (координаты и радиусы колонн заданы) необходимо разместить круглый фонтан максимального радиуса.

Администрация одного института решила построить в холле фонтан. По плану администрации, фонтан должен иметь форму круга с максимально возможным радиусом. Дизайнеру сообщили, что холл института имеет вид прямоугольника, размером \(X\)×\(Y\) метров. Однако когда дизайнер стал выбирать место для фонтана, он столкнулся с серьезной проблемой: в холле института обнаружилось \(N\) круглых колонн, снести которые не представляется возможным.

Таким образом, у него появилась проблема: где следует поместить фонтан, чтобы он имел максимально возможный радиус и не имел ненулевого по площади пересечения с колоннами. Вам предстоит помочь ему в решении этой нелегкой задачи.

Входные данные

В первой строке входных данных содержатся вещественные числа \(X\) и \(Y\), 1 <= \(X\), \(Y\) <= \(10^4\) . Будем считать, что прямоугольник холла расположен на координатной сетке так, что его углы имеют координаты (0, 0), (\(X\), 0), (\(X\), \(Y\)) и (0, \(Y\)).

Во второй строке задается число \(N\) (0 <= \(N\) <= 10) - количество колонн. Следующие \(N\) строк содержат параметры колонн - \(i\)-я строка содержит три вещественных числа \(X_i\), \(Y_i\) и \(R_i\) - координаты центра и радиус \(i\)-й колонны (\(R_i\) <= \(X_i\) <= \(X\)-\(R_i\), \(R_i\) <= \(Y_i\) <= \(Y\)-\(R_i\), 0.1 <= \(R_i\) <= min(\(X\) / 2, \(Y\) / 2); для любых \(i\) ≠ \(j\) sqrt( (\(X_i\) - \(X_j\))2 + (\(Y_i\) - \(Y_j\))2 )>= \(R_i\) + \(R_j\)). Все вводимые числа разделены пробелами.

Выходные данные

Выведите три вещественных числа: \(X_F\), \(Y_F\) и \(R_F\) - координаты центра и радиус фонтана. Фонтан должен быть полностью расположен внутри холла (допускается касание стен) и не иметь ненулевого пересечения ни с одной из колонн (допускается касание). Радиус фонтана должен быть максимален. Разделяйте числа пробелами и/или переводами строки. Если решений несколько, выведите любое из них.

Примеры
Входные данные
10 10
0
Выходные данные
5.000 5.000 5.000
Входные данные
1 1000
0
Выходные данные
0.500 0.500 0.500
Входные данные
10 10
4
1 1 1
9 9 1
1 9 1
9 1 1
Выходные данные
5.000 5.000 4.657
#860
Путь через горы
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Поверхность Земли в горной местности можно представить в виде ломаной линии. Вершины ломаной расположены в точках (x1, y1), (x2, y2),…,(xN, yN), при этом xi<xi+1.

Обычный горный маг находится в точке (x1, y1) и хочет попасть в точку (xN, yN). При этом он может перемещаться только пешком. Он может ходить по поверхности Земли (т.е. вдоль ломаной). А может сотворить в воздухе мост и пройти по нему. Мост может соединять две вершины ломаной: мост не может начинаться и заканчиваться не в вершине ломаной, и мост не может проходить под землей (в том числе не может быть туннелем в горе), но мост может каким-то своим участком проходить по поверхности земли. Длина моста не может быть больше R. Суммарно маг может построить не более K мостов.

Какое наименьшее расстояние придется пройти магу, чтобы оказаться в точке (xN, yN).

Входные данные

Вводится сначала натуральное число N (2≤N≤100). Затем водится натуральное число K (1≤K≤100) — максимальное количество мостов. Далее вводится целое число R (0≤R≤10000) — максимальная возможная длина моста. Далее вводятся координаты (x1, y1), (x2, y2),…,(xN, yN). Все координаты – целые числа, не превышающие по модулю 10000, для всех i от 1 до N–1: xi<xi+1.

Выходные данные

Выведите одно число — минимальную длину пути, которую придется пройти магу (как по земле, так и по мостам). Ответ выведите не менее чем с 5 цифрами после десятичной точки.

Примеры

Входных данные

Выходные данные

5 2 5

0 0

2 2

3 -1

4 1

5 0

6.47871

9 2 3

1 2

2 1

3 3

5 -1

6 2

7 0

8 1

9 0

10 1

14.93498
Страница: << 1 2 3 4 5 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест