Как вы помните, Джонни работает в министерстве финансов одной небольшой страны. По роду службы ему приходится инспектировать отечественные авиакомпании и изучать маршруты, которые те предлагают.
В стране есть n городов. По государственным законам авиакомпания должна предоставлять услуги двустороннего перелёта между некоторыми парами городов, причём в целях унификации и стандартизации продолжительность любого полёта должна составлять ровно один день.
Авиакомпания называется крупной, если с помощью рейсов этой компании можно добраться из любого города страны до любого другого. Крупная авиакомпания называется экономной, если при этом количество маршрутов, ею предлагаемое, минимально возможное, которое может быть у крупной компании.
Государственная антимонопольная служба возбудила расследование против крупной авиакомпании «Aero-float». Ей предъявлено обвинение в излишней неэкономности. Джонни было поручено проинспектировать «Aero-float» в целях обнаружения финансовых махинаций, но авиакомпания отказалась раскрывать полный список предоставляемых ею прямых рейсов. После продолжительных переговоров руководство компании согласилось сообщить Джонни информацию о минимально возможном количестве перелётов между каждой парой городов, если использовать только прямые рейсы «Aero-float».
Используя эту информацию, помогите Джонни установить, может ли компания «Aero-float» быть экономной или нет? Более формально, установите, существует ли набор рейсов, при котором число рейсов в кратчайших маршрутах именно такие, как было сообщено Джонни, и при котором компания является экономной?
В первой строке содержится единственное целое число n (2 ≤ n ≤ 250) — количество городов в стране.
Далее идёт n строк, содержащих по n целых чисел Ti, j: j-е число в i-й строке равняется минимальному количеству перелётов, требуемому на перемещение из i-го города в j-й.
Гарантируется, что предоставленная информация корректна, то есть существует некоторый набор рейсов, который соответствует данному набору чисел Ti, j.
Выведите «YES», если компания «Aerofloat» может являться экономной, или «NO» в противном случае.
5
0 2 1 1 1
2 0 1 3 3
1 1 0 2 2
1 3 2 0 2
1 3 2 2 0
YES
4
0 1 1 1
1 0 2 2
1 2 0 1
1 2 1 0
NO
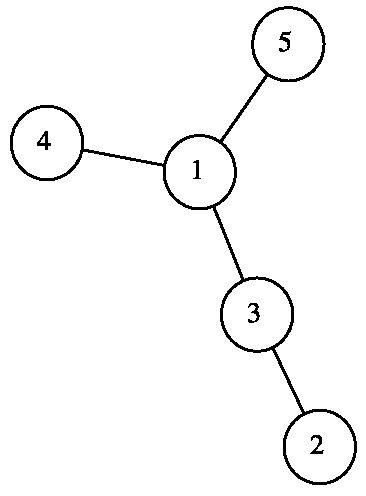
Для первого примера ниже приведён возможный вариант предлагаемых компанией маршрутов, при котором она является экономной. На рисунке соединены те пары городов, между которыми есть прямые рейсы.
Будущие программисты Андрей и Борис вчера впервые поехали кататься с родителями по новой кольцевой дороге. Каждый из них выехал на дорогу в определённом месте, сделал полный круг и вернулся домой. От скуки они оба считали фонарные столбы, расположенные посередине дороги между встречными полосами движения, так что все N фонарных столбов у каждого из мальчиков получили номера от 1 до N . Но само значение N они не запомнили. При этом два столба обоим мальчикам запомнились особенно: на одном из них висел яркий плакат ко Дню города, а на другом — флаг Москвы. Каждый из мальчиков записал себе в тетрадку номер каждого из этих двух столбов.
Сегодня обе семьи, Андрея и Бориса, пошли на выставку кошек, и там мальчики, обсудив свои поездки, задались вопросом: сколько же всего фонарных столбов на новой кольцевой дороге? Единственное, что они смогли выяснить, в одном ли направлении ехали они по дороге.
Так сложилось, что Андрей — ваш младший брат, поэтому именно вам предстоит ответить на вопрос мальчиков. У вас есть серьёзное подозрение, что может не получиться однозначно найти ответ, а мальчики боятся больших чисел, поэтому вы решили сказать им лишь минимальное из возможных значений числа N .
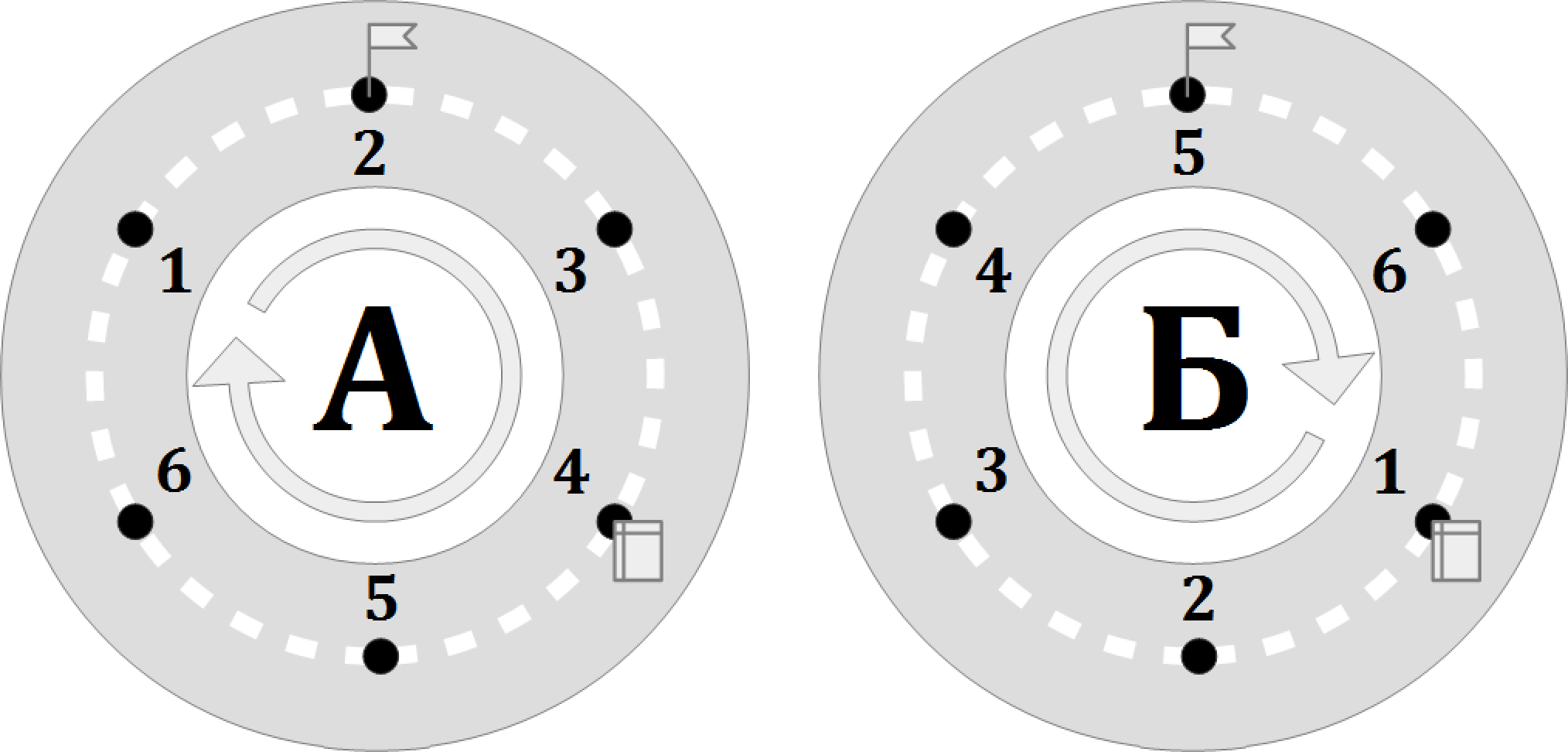
В этом примере N = 6 , A p = 4 , A f = 2 , B p = 1 , B f = 5 .
Первая строка входного файла содержит единственное целое число D , которое равно 1 , если мальчики ехали в одном направлении, и - 1 , если в разных. Вторая строка содержит 4 натуральных числа A p , B p , A f , B f , каждое из которых не превосходит 10 9 : A p — номер столба с плакатом в нумерации Андрея, B p — номер этого столба в нумерации Бориса, A f — номер столба с флагом в нумерации Андрея, B f — номер этого столба в нумерации Бориса. Соседние числа в строке разделены одним пробелом. Плакат и флаг могли оказаться на одном столбе — в этом случае каждый из мальчиков должен был бы получить два одинаковых числа, т. е. A p = A f и B p = B f .
Выведите единственное натуральное число N — минимально возможное количество столбов. Если мальчики где-то ошиблись, и таких чисел, как у них, не могло получиться ни при каком зна-че-нии N , выведите число - 1 .
1 4 1 2 5
6
-1 4 9 4 7
-1
Команда туристического клуба «В гору пойдёт!» только что вернулась из очередного похода. Прямо сейчас участники экспедиции с жаром спорят о том, какой же горный хребет они покорили.
Достоверно известно, что на маршруте было N стоянок, причём все — на разной целочисленной высоте от 1 до N над уровнем моря. Альпинисты заблаговременно прибыли на место первой стоянки, а потом шли по маршруту в течении N - 1 дня: в первый день они шли от 1 -й стоянки до 2 -й, во второй — от 2 -й до 3 -й и так далее, пока в последний день не совершили переход от стоянки под номером N - 1 до стоянки под номером N , завершив этим свой маршрут.
Участники экспедиции пытаются понять, на какой высоте находилась каждая стоянка. В их распоряжении имеются записи в журнале, содержащие информацию о том, в какой день они шли в гору, а в какой — спускались.
Помогите альпинистам! Подскажите им хоть какой-нибудь вариант маршрута, не противоречащий записям в журнале.
В первой строке входного файла содержится натуральное число N — количество стоянок на маршруте ( 2 ≤ N ≤ 1 000 000 ). Во второй строке входного файла содержится последовательность длины N - 1 , состоящая из знаков « < » и « > ». Если на i -м месте в этой последовательности стоит знак « < », то в i -й день альпинисты шли в гору, а знак « > » означает, что в i -й день они спускались.
Выведите строку, содержащую N различных целых чисел от 1 до N , разделённых пробелами, — маршрут, по которому могли пройти альпинисты. Маршрут описывается высотами стоянок в том порядке, в котором их посетили участники экспедиции.
5 >><>
3 2 1 5 4
Что может быть проще простого числа? Казалось бы, объяснить, что такое простое число, можно даже человеку, совершенно далёкому от математики: целое число называется простым, если оно не меньше двух и не делится ни на какое целое положительное число, кроме единицы и самого себя. Это определение будет понятно даже третьекласснику, только-только познакомившемуся с делением. Что может быть проще? Но, как часто случается в математике, за кажущейся простотой определения скрывается очень глубокая теория с множеством нетривиальных фактов, многие из которых остаются недоказанными и по сей день.
Прочитав популярную книгу Д. Дербишира
«Простая одержимость»
, Леопольд узнал следующий занятный факт. Оказывается, существует
Теорема о распределении простых чисел
, гласящая, что количество простых чисел, не превышающих
N
, можно очень точно оценить как
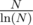 . Например, начиная с
N
> 5000
, эта формула даёт ошибку, не более чем в 15% от реального значения. Более того, с ростом
N
относительная погрешность такой оценки падает, стремясь к нулю.
. Например, начиная с
N
> 5000
, эта формула даёт ошибку, не более чем в 15% от реального значения. Более того, с ростом
N
относительная погрешность такой оценки падает, стремясь к нулю.
Леопольд крайне заинтересовался простыми числами и связанной с ними теорией. Он решил выдвинуть какую-нибудь не менее важную и серьёзную гипотезу, а потом доказать её, и назвать полученный факт теоремой Леопольда. Для этого ему нужна помощь в отыскании закономерностей, описывающих простые числа. Он просит вас написать для него программу, которая ищет для него Q отрезков, i -й из которых состоит из L i последовательных натуральных чисел и содержит определённое количество K i простых чисел. Для простоты анализа он просит вас ограничиться в поисках первыми десятью миллионами чисел. Помогите ему, и, возможно, вам с ним удастся оставить след в истории!
В первой строке входного файла задано целое число Q ( 1 ≤ Q ≤ 100 000 ) "— количество отрезков, которые требуются Леопольду.
В каждой из последующих Q строк задано по два целых числа L и K ( 7000 ≤ K ≤ L ≤ 100 000 ). Обратите внимание , подобные ограничения даны не случайно: Леопольд знает, что нередко закономерности начинают проявляться только при больших значениях.
На каждый запрос Леопольда выведите в отдельной строке начальное и конечное число требуемого отрезка, либо - 1 , если его не существует среди первых десяти миллионов чисел. Если требуемых отрезков несколько, выведите любой.
3 8000 8000 80000 7654 100000 7000
-1 3632 83631 1482488 1582487
Склад завода по изготовлению матрёшек переполнен! Нужно как-то освобождать место, поэтому директор завода принял волевое решение продать абсолютно всё, что там лежит. Больше всего места на складе занимают заготовки для матрёшек — нераскрашенные статуэтки целых положительных размеров, которые можно вставлять друг в друга. Увы, в таком неприглядном виде покупать их никто не хочет.
К счастью, завод сотрудничает с союзом художников по матрёшкам. В частности, был заключён договор, позволяющий заводу заказывать роспись матрёшек. В договоре указано, что матрёшка — это упорядоченный набор из M статуэток ( 1 ≤ M ) размеров a 1 , a 2 , ..., a M , где a 1 + 1 = a 2 , a 2 + 1 = a 3 , ..., a M - 1 + 1 = a M . Там же прописано, что стоимость раскрашивания одной матрёшки равна одному тугрику, при этом количество статуэток, входящих в матрёшку, значения не имеет.
Получается, что для того чтобы продать всё содержимое склада, нужно сначала собрать заготовки в матрёшки и заказать роспись полученных матрёшек у художников. Помогите директору завода сделать это, потратив как можно меньше тугриков!
В первой строке входного файла содержится число N — количество заготовок на складе ( 1 ≤ N ≤ 2·10 5 ). Во второй строке содержатся N целых чисел s 1 , s 2 , ..., s N , где s i — это размер i -й заготовки ( 1 ≤ s i ≤ 2·10 5 ).
В первой строке выходного файла выведите целое число T — минимальное количество тугриков, которое нужно заплатить художникам.
В следующих T строках выведите описания матрёшек, которые завод закажет у союза художников. Описание матрёшки состоит из строки, содержащей два разделённых пробелом числа, где первое число — размер самой маленькой статуэтки в матрёшке, а второе число — размер самой большой статуэтки в матрёшке.
5 3 2 1 2 5
3 2 2 1 3 5 5