Тимофей — настоящий сладкоежка. Сегодня он купил большой и вкусный круглый торт с клубникой, чтобы полакомиться самому и угостить друзей.

Однако Тимофей угощает друзей очень изощренным способом. А именно, он отрезает кусочки с краев торта прямолинейными разрезами ножа. При этом, чтобы разрезы получились красивыми, нож нужно вести непрерывно, разрезы не должны друг друга пересекать, а закончить процесс отрезания нужно в начальной его точке. Более того, так как Тимофей — большой любитель клубники, то он хочет, чтобы все ягоды оказались внутри центрального куска тортика, который, конечно же, достанется ему самому.

Однако оказалось, что разрезать торт таким образом весьма непросто. Помогите Тимофею! Быть может, в награду он и вас угостит кусочком этого замечательного тортика.

Будем считать, что торт является кругом на плоскости, а ягоды представляют собой точки. Необходимо построить любой выпуклый многоугольник, вершины которого лежат на окружности, ограничивающей круг, а все заданные точки находятся внутри него или на его границе.

Будущие программисты Андрей и Борис вчера впервые поехали кататься с родителями по новой кольцевой дороге. Каждый из них выехал на дорогу в определённом месте, сделал полный круг и вернулся домой. От скуки они оба считали фонарные столбы, расположенные посередине дороги между встречными полосами движения, так что все N фонарных столбов у каждого из мальчиков получили номера от 1 до N . Но само значение N они не запомнили. При этом два столба обоим мальчикам запомнились особенно: на одном из них висел яркий плакат ко Дню города, а на другом — флаг Москвы. Каждый из мальчиков записал себе в тетрадку номер каждого из этих двух столбов.

Сегодня обе семьи, Андрея и Бориса, пошли на выставку кошек, и там мальчики, обсудив свои поездки, задались вопросом: сколько же всего фонарных столбов на новой кольцевой дороге? Единственное, что они смогли выяснить, в одном ли направлении ехали они по дороге.

Так сложилось, что Андрей — ваш младший брат, поэтому именно вам предстоит ответить на вопрос мальчиков. У вас есть серьёзное подозрение, что может не получиться однозначно найти ответ, а мальчики боятся больших чисел, поэтому вы решили сказать им лишь минимальное из возможных значений числа N .

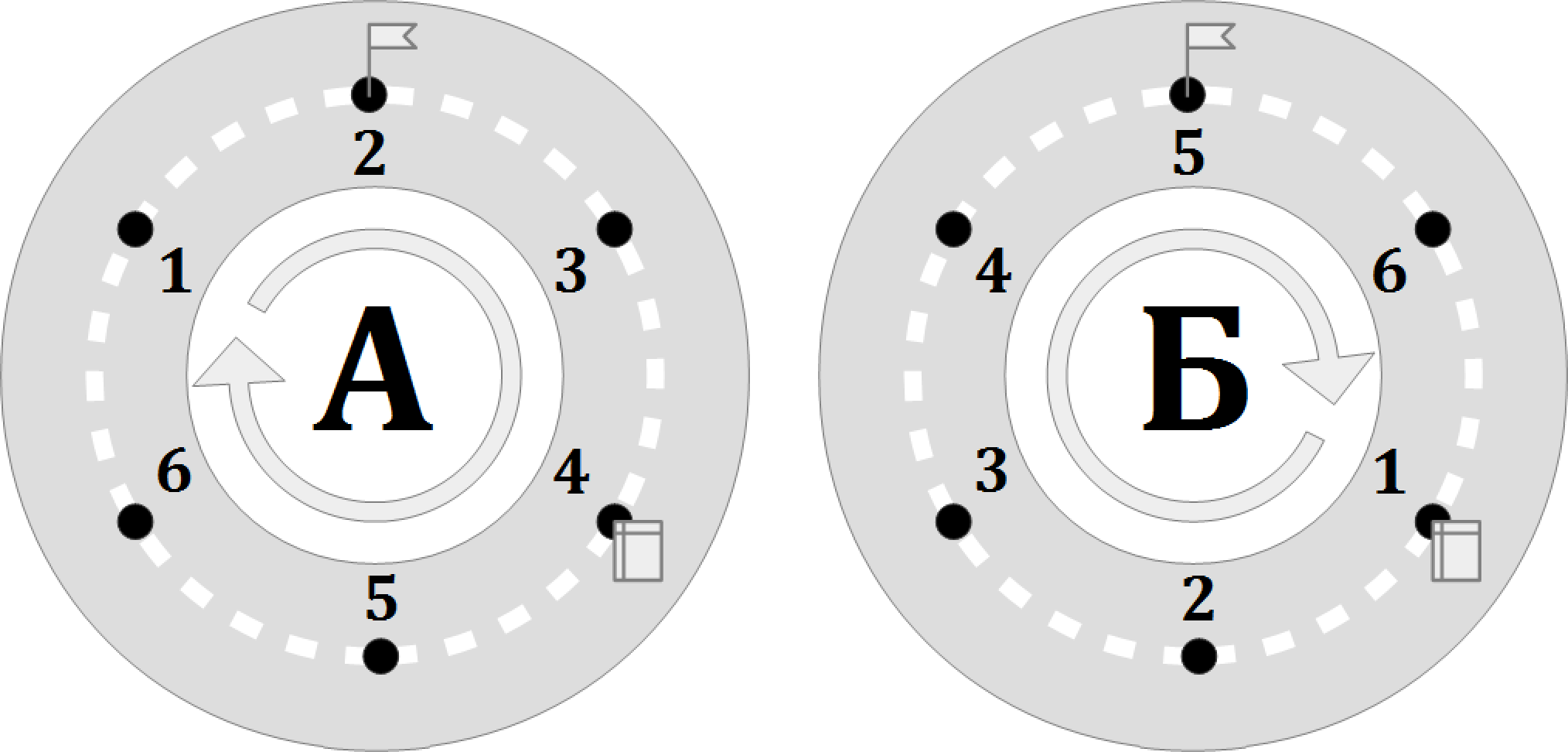
В этом примере N = 6 , A _p = 4 , A _f = 2 , B _p = 1 , B _f = 5 .

Команда туристического клуба «В гору пойдёт!» только что вернулась из очередного похода. Прямо сейчас участники экспедиции с жаром спорят о том, какой же горный хребет они покорили.

Достоверно известно, что на маршруте было N стоянок, причём все — на разной целочисленной высоте от 1 до N над уровнем моря. Альпинисты заблаговременно прибыли на место первой стоянки, а потом шли по маршруту в течении N - 1 дня: в первый день они шли от 1 -й стоянки до 2 -й, во второй — от 2 -й до 3 -й и так далее, пока в последний день не совершили переход от стоянки под номером N - 1 до стоянки под номером N , завершив этим свой маршрут.

Участники экспедиции пытаются понять, на какой высоте находилась каждая стоянка. В их распоряжении имеется запись в журнале, содержащая информацию о том, сколько дней они шли в гору, а сколько — спускались.

Помогите альпинистам! Подскажите им хоть какой-нибудь вариант маршрута, не противоречащий записи в журнале.

Что может быть проще простого числа? Казалось бы, объяснить, что такое простое число, можно даже человеку, совершенно далёкому от математики: целое число называется простым , если оно не меньше двух и не делится ни на какое целое положительное число, кроме единицы и самого себя. Это определение будет понятно даже третьекласснику, только-только познакомившемуся с делением. Что может быть проще? Но, как часто случается в математике, за кажущейся простотой определения скрывается очень глубокая теория с множеством нетривиальных фактов, многие из которых остаются недоказанными и по сей день.

Леопольд очень интересуется всем, что связано с простыми числами. Недавно он узнал про Постулат Бертрана — оказывается, на отрезке между N и 2 N всегда найдётся хотя бы одно простое число! Несмотря на простую формулировку и интуитивную очевидность этого утверждения, сформулированного французским математиком Жозефом Луи Франсуа Бертраном, оно было доказано только в середине 19 века русским математиком Пафнутием Львовичем Чебышёвым.

Впечатлённый тем, как можно увековечить своя имя на страницах истории математики, Леопольд решил выдвинуть какую-нибудь не менее важную и серьёзную гипотезу, а потом доказать её, и назвать полученный факт теоремой Леопольда. Для этого ему нужна помощь в отыскании закономерностей, описывающих простые числа. Он просит вас написать для него программу, которая ищет отрезок из L последовательных натуральных чисел, содержащий ровно K простых чисел. Чтобы результаты было легче анализировать, он просит вас ограничиться в поисках первыми тридцатью тысячами натуральных чисел. Помогите ему, и, возможно, и вам удастся оставить след в истории!

Склад завода по изготовлению матрёшек переполнен! Нужно как-то освобождать место, поэтому директор завода принял волевое решение продать абсолютно всё, что там лежит. Больше всего места на складе занимают заготовки для матрёшек — нераскрашенные статуэтки целых положительных размеров, которые можно вставлять друг в друга, если размер одной меньше чем размер другой. Увы, в таком неприглядном виде покупать их никто не хочет.

К счастью, завод сотрудничает с союзом художников по матрёшкам. В частности, был заключён договор, позволяющий заводу заказывать роспись матрёшек. В договоре указано, что матрёшка — это упорядоченный набор из M статуэток ( 1 ≤ M ) размеров r ₁ < r ₂ < r ₃ < ... < r _M . Там же прописано, что стоимость раскрашивания одной матрёшки равна одному тугрику, при этом количество статуэток, входящих в матрёшку, значения не имеет.

Получается, что для того чтобы продать всё содержимое склада, нужно сначала собрать заготовки в матрёшки и заказать роспись полученных матрёшек у художников. Помогите директору завода сделать это, потратив как можно меньше тугриков!