Игорь работает младшим лаборантом в НИИ ихтиологии. Ему вверены \(n\) аквариумов, стоящих в ряд, в каждом из которых живет колония рыбок гуппи. Про каждую колонию заранее известна ее численность.
В лабораторных условиях НИИ ихтиологии колония рыбок гуппи растет по следующему правилу: достигнув популяции в \(f\) рыбок, колония живет в течении \(max(1000 - f, 1)\) секунд, после чего на свет появляется новая рыбка. От начального момента времени до рождения первой рыбки колония размера \(f\) также ждет \(max(1000 - f, 1)\) секунд.
Например, колония с начальным размером 996 будет размножаться следующим образом:
| момент времени | размер колонии | время до очередной рыбки |
|---|---|---|
| 0 | 996 | 4 |
| 4 | 997 | 3 |
| 7 | 998 | 2 |
| 9 | 999 | 1 |
| 10 | 1000 | 1 |
| 11 | 1001 | 1 |
| 12 | 1002 | 1 |
| ... | ... | ... |
Появление на свет каждой новой рыбки Игорь должен фиксировать в специальном журнале. Будем считать, что запись он делает мгновенно, но при этом он должен в момент рождения новой рыбки находиться рядом с аквариумом, в котором это произошло.
На перемещение от одного аквариума к соседнему у Игоря уходит одна секунда. В начальный момент времени Игорь стоит около первого аквариума.
Вычислите, в течение какого наибольшего периода времени Игорь сможет добросовестно выполнять свою работу.
В первой строке входного файла содержится целое число \(n\) (\(2 \le n \le 50\)) - количество аквариумов с рыбками гуппи в НИИ ихтиологии. Каждая из следующих \(n\) строк содержит одно целое число \(a_i\) (\(1 \le a_i \le 2007\)) - численность \(i\)-й колонии.
В выходной файл выведите момент времени, когда родится первая рыбка гуппи, запись о рождении которой Игорь сделать не сможет.
В приведенном примере Игорь сначала ждет у первого аквариума появления рыбки на 4-й секунде. После этого он бежит к третьему аквариуму (на это у него уходит 2 секунды) и как раз успевает к рождению рыбки на 6-й секунде. Однако вернуться к первому аквариуму, где следующая рыбка родится на 7-й секунде, он уже не успевает.
3 996 1 994
7
Антон - большой любитель компьютерных игр. Совсем недавно вышла новая игра Heroes of Keyboard and Mouse, и он, конечно же, сразу ее купил и установил на свой компьютер. Эта игра относится к жанру квестов, и поэтому ее прохождение сводится к последовательному выполнению ряда заданий (квестов).
Один из квестов, над которым Антон бьется уже не первый день состоит в том, что требуется открыть замок. Замок состоит из \(n\) шестеренок, стоящих в ряд - \(i\)-ая из шестеренок имеет \(s_i\) зубцов, на каждом из которых написано число от \(0\) до \(s_i - 1\). Первая шестеренка зацеплена только со второй, вторая зацеплена с первой и третьей, третья - со второй и четвертой, ..., \((n-1)\)-ая - с \((n-2)\)-ой и \(n\)-ой, \(n\)-ая только с \((n-1)\)-ой.
На замке имеется \(n\) окошечек и \(n\) ручек - в \(i\)-ое окошко можно видеть число, написанное на одном из зубцов \(i\)-ой шестеренки, а с помощью \(i\)-ой ручки можно поворачивать \(i\)-ую шестеренку. При этом числа на шестеренках расположены таким образом, что если до поворота \(i\)-ой из них по часовой стрелке на одно деление в \(i\)-ом окошке было видно число \(x\), то после поворота будет видно число \((x+1) \bmod s_i\). Аналогично, после поворота против часовой стрелки на одно деление вместо числа \(x\) будет видно число \((x-1+s_i) \bmod s_i\). Разумеется, если шестеренку повернуть по часовой стрелке, то непосредственно зацепленные с ней шестеренки повернутся против часовой стрелки, и наоборот, если шестеренку повернуть против часовой стрелки, то они повернутся по часовой стрелке. Слева на рис.1 показано положение шестеренок до поворота первой из них по часовой стрелке, справа на рис. 1 показано положение шестеренок после указанного поворота. Более толстыми линиями нарисован тот зубец шестеренки, число на котором видно в соответствующее окошко замка.
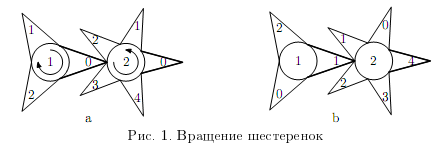
Изначально замок находится в состоянии, в котором в \(i\)-ое окошко видно число \(a_i\). Для того, чтобы его открыть, необходимо перевести его в состояние, в котором в \(i\)-ое окошко видно число \(b_i\).
С помощью \(i\)-ой ручки можно поворачивать \(i\)-ую шестеренку. Разумеется, если повернуть \(i\)-ую шестеренку, то придут в движение и все шестеренки, с которыми она соединена - напрямую или через другие шестеренки. Поворот любой шестеренки на одно деление занимает одну секунду. Кроме этого, если \(i\)-ая шестеренка находится в таком состоянии, что в \(i\)-ое окошко видно число \(b_i\) (то есть, она находится в положении, соответствующем требуемому состоянию замка), то ее можно вдавить, нажав на ее ручку. В результате этого \(i\)-ая шестеренка перестает быть соединенной с \((i-1)\)-ой и \((i+1)\)-ой (если, конечно, они существуют). Вдавленная шестеренка остается в таком состоянии навсегда. На то, чтобы нажать на ручку и вдавить шестеренку требуется \(k\) секунд. На рис. 2 слева показано положение шестеренок до вдавливания второй из них, а справа - после вдавливания и после поворота первой по часовой стрелке, а третьей - против. Отметим, что после вдавливания второй шестеренки первая и третья вращаются независимо друг от друга.
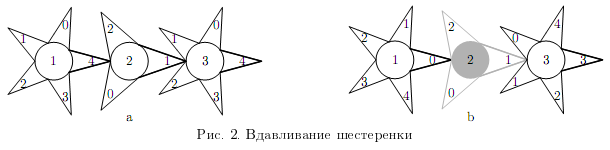
Для того, чтобы выполнить квест, Антону необходимо открыть замок как можно быстрее. Напишите программу, которая по описанию замка, его начального состояния и требуемого состояния, вычислит минимальное время, за которое Антон может открыть замок.
Первая строка входного файла содержит два целых числа: \(n\) и \(k\) (\(1 \le n \le 25\), \(1 \le k \le 100\)). Вторая строка входного файла содержит \(n\) чисел: \(s_1\), \(s_2\), ..., \(s_n\) - размеры шестеренок. Все \(s_i\) - целые числа от 3 до 10. Третья строка входного файла содержит \(n\) целых чисел \(a_1\), \(a_2\), ..., \(a_n\) - начальные положения шестеренок (для всех \(a_i\) выполняются неравенства \(0 \le a_i < s_i\)). Четвертая строка входного файла содержит \(n\) целых чисел \(b_1\), \(b_2\), ..., \(b_n\) - требуемые положения шестеренок (для всех \(b_i\) выполняются неравенства \(0 \le b_i < s_i\)).
В выходной файл выведите минимальное количество времени, которое необходимо для того, чтобы открыть замок.
2 2 3 5 0 0 1 1
4
3 2 3 3 3 0 0 0 1 1 1
5
На день рождения юному технику Мише подарили машинку с радиоуправлением. Мише быстро наскучило гонять машинку туда-сюда по комнате, и он соорудил специальную трассу. Для этого он разбил комнату на квадратные ячейки, некоторые из них оставив пустыми, а в некоторые поставив препятствия. Целую неделю Миша каждый день улучшал свой рекорд по прохождению трассы. Но каково же было разочарование Миши, когда к нему в гости пришел Тима со своей машинкой и побил его рекорд. Стало понятно, что машинку необходимо модернизировать.
На пробных испытаниях, которые были произведены через день, Миша обнаружил, что машинка действительно ездит лучше, однако ее поведение несколько изменилось. На пульте теперь функционируют только четыре кнопки: вперед, назад, вправо, влево. При нажатии на них машинка едет по направлению к соответствующей стене комнаты, являющейся одновременно границей трассы, точно перпендикулярно ей. Машинка разгоняется до такой скорости, что перестает реагировать на другие команды, врезается в ближайшее препятствие или стену и отскакивает от нее на половину пройденного расстояния, то есть если между машинкой и стеной было x пустых клеток, то после отскока она остановится на клетке, от которой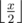 
клеток до стены (⌊ x⌋ означает округление вниз, например 
, 
).
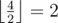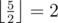Теперь Мише интересно, какое минимальное количество раз необходимо нажать на кнопку пульта, чтобы машинка, начав в клетке старта, остановилась в клетке финиша.
Первая строка входного файла содержит два целых числа n и m — размеры трассы (2 ≤ m, n ≤ 20). Следующие n строк содержат по m символов каждая: символ «.» соответствует пустой клетке, «#» — препятствию, а «S» и «T» — клетке старта и клетке финиша соответственно.
В выходной файл выведите минимальное количество нажатий на кнопки пульта для проведения машинки по трассе от старта до финиша.
Если доехать от старта до финиша невозможно, выведите - 1.
5 5 S#..T .#.## ..... .##.# .#...
6
Петя и Вася играют в забавную игру с карточками. Игра очень простая. Есть колода карт, на каждой из которых написана буква латинского алфавита. Карты перемешиваются, выдаются участникам и они составляют из них слова.
Вася хочет немножко смухлевать. Он знает, в каком порядке лежат карты в колоде и как Петя их мешает. По этим данным он хочет узнать, как будут лежать карты после перемешивания.
Перемешивание карт происходит в несколько этапов. На каждом этапе Петя сначала по очереди берет карты из колоды от верхней к нижней и раскладывает их на две стопки: одну налево, одну направо, одну налево, одну направо. После этого он кладет левую стопку на правую. Эти действия повторяются k раз.
Помогите Васе определить, как будут лежать карты в колоде после перемешивания.
Первая строка входного файла содержит строку, описывающую состояние колоды до перемешивания. Строка состоит из заглавных латинских букв. i-я буква строки соответствует i-й карте от низа колоды. Длина строки не превышает 100 символов.
Вторая строка содержит целое число k (1 ≤ k ≤ 100).
В выходной файл выведите состояние колоды после перемешивания в том же формате, что и во входном файле.
ABCDEFG 1
FDBGECA
Кальпас — обычный говорящий пес, который живет в зоопарке на Марсе. К сожалению, условия содержания животных там не самые лучшие. Кальпаса выпускают на прогулку только раз в день, да и то, «выпускают» — не самое лучшее слово. Двое охранников: Вася и К-20071027, надевают на Кальпаса специальный ошейник и выводят его во двор. Ошейник полностью контролирует перемещения пса: в любой момент Кальпас находится в точности на середине отрезка между своими охранниками.
К сожалению, тот, кто изобрел этот ошейник, совершенно не думал о собаках. Как любому псу, Кальпасу хочется за время своей прогулки пробежать по строго определенному пути. Как же ему это сделать? Кальпас решил договориться со своими охранниками. Поскольку Вася — робот, который движется каждый день по заданному в его программе маршруту с постоянной скоростью, договориться с ним нет никакой возможности. Единственное, что остается Кальпасу — договориться с К-20071027.
Для того, чтобы подготовиться к переговорам, Кальпас хочет выяснить, путь какой длины должен пройти К-20071027, чтобы Кальпас двигался по намеченному пути с постоянной скоростью.
Входной файл содержит описание двух маршрутов, являющихся ломаными линиями: пути, по которому хочет пройти Кальпас и маршрута, по которому ежедневно ходит Вася.
Первая строка описания каждого из маршрутов содержит количество вершин ломаной, а последующие задают координаты этих вершин. Количество вершин в каждой ломаной не превышает 100, координаты точек целые и по модулю не превышают 1000.
В выходной файл выведите длину пути, который должен будет пройти К-20071027 с точностью не менее 10 - 6.
4 0 0 0 6 6 6 6 0 3 0 0 3 3 6 0
30.59411708155670700000