Джон работает на огромной парковке. Парковка представляется собой прямоугольное поле \(n \times m\), разбитое на \(n \times m\) квадратных позиций размера \(1 \times 1\). Одну из угловых позиций занимает выезд с парковки.

Машин на парковке много и вывести машину не так уж просто. Единственное, что Джон может сделать — это переместить один из автомобилей на соседнюю позицию, если она свободна. Соседними считаются позиции, имеющие общую сторону. Однако задача усложняется наличием на парковке столбов. На позиции, где стоят столбы, нельзя поставить машину. Парковка вся занята машинами и столбами и единственное свободное место — выезд с парковки. Задача Джона — вывести с парковки один из автомобилей. Помогите ему узнать, какое минимальное число действий ему придется совершить.

Директор школы «Лицей Программистов» города Линейска сумел привить ученикам этой школы хорошую дисциплину, но, несмотря на это, многие ученики продолжают опаздывать на уроки.

В Линейске есть всего одна главная улица, на которой расположен и сам лицей, и живут все его ученики. Дисциплинированные школьники выходят из своих домов в одно и то же время. Но, к сожалению, все они живут на разном расстоянии от школы и добираются с разной, но постоянной скоростью (среди учеников есть как весьма неторопливые, так и будущая чемпионка мира по бегу на 100 метров Маша Гайка).

Для улучшения ситуации с опозданиями школа купила один веломобиль, который взялся водить сторож школы. Веломобиль способен помимо водителя перевозить одного школьника. Веломобиль перемещается с постоянной скоростью \(v\).

Ночь веломобиль проводит в школьном гараже, а утром, ровно в тот момент, когда все ученики выходят из своих домов, отправляется им навстречу, чтобы подвезти какого-нибудь школьника. Конечно же, ему приходится подвозить школьника прямо до ворот школы, потому как никто не хочет быть высаженным посреди пути. После того, как веломобиль помог одному ученику быстрее добраться в учебное заведение, он снова может ехать навстречу следующему опаздывающему человеку.

Директор хочет начинать занятия как можно раньше, но для этого нужно, чтобы все ученики добрались до лицея. Он поручил вам помочь составить план, по которому должен действовать водитель веломобиля, чтобы время прибытия последнего школьника в школу было минимальным.

Новый мэр крупного города Флатбурга Иван Котянин начал свою работу с решения проблем с пробками в городе. Как и в любом крупном городе, во Флатбурге есть кольцевая автодорога. Во Флатбурге она представляет собой монотонный многоугольник. Монотонным называется многоугольник, с которым каждая прямая, проходящая строго с севера на юг, имеет не более двух общих точек.

После совещания с правительством города было принято решение построить новую магистраль — скоростной диаметр, который вел бы строго с севера на юг и соединял две точки кольцевой автодороги.

Помимо борьбы с пробками решено было обновить рекорд по протяженности самой длинной магистрали, проложенной с севера на юг. Для того чтобы обновить рекорд необходимо построить магистраль длиной хотя бы \(d\) километров, а поскольку лишних денег в бюджете Флатбурга не так уж и много, решено было построить дорогу длиной ровно \(d\).

Министр транспорта Флатбурга решил предоставить мэру все варианты строительства новой дороги. Для начала он решил подсчитать, сколько существует способов построить магистраль. Помогите министру.

Сергей работает системным администратором в очень крупной компании. Естественно, в круг его обязанностей входит резервное копирование информации, хранящейся на различных серверах и «откат» к предыдущей версии в случае возникновения проблем.

В данный момент Сергей борется с проблемой недостатка места для хранения информации для восстановления. Он решил перенести часть информации на новые сервера. К сожалению, если что-то случится во время переноса, он не сможет произвести откат, поэтому процедура переноса должна быть тщательно спланирована.

На данный момент у Сергея хранятся \(n\) точек восстановления различных серверов, пронумерованных от 1 до \(n\). Точка восстановления с номером \(i\) позволяет произвести откат для сервера \(a_i\). Сергей решил разбить перенос на этапы, при этом на каждом этапе в случае возникновения проблем будут доступны точки восстановления с номерами \(l, l + 1, \ldots, r\) для некоторых \(l\) и \(r\).

Для того, чтобы спланировать перенос данных оптимальным образом, Сергею необходимо научиться отвечать на запросы: для заданного \(l\), при каком минимальном \(r\) в процессе переноса будут доступны точки восстановления не менее чем \(k\) различных серверов.

Помогите Сергею.

Погостив пару недель у Темного Властелина и прослушав истории о всех его похождениях за последние годы, сэр Петрейн понял, что он уже давно не совершал никаких подвигов. Посидев за чашкой чая и тщательно обсудив будущий подвиг, они решили, что Петрейну нужно победить ужасного дракона, который уже давно терроризирует западные окраины Личного королевства. И вот он отправился готовиться к великому походу.

Но какой рыцарь идет на дракона без рыцарского обмундирования? Поэтому Петрейну нужны доспехи, щит и меч. Всем известно, что чем щит больше, тем эффективней будет он в бою. Сейчас у Петрейна есть два треугольных щита, но он считает их недостаточно надежными и хочет сделать из них один.

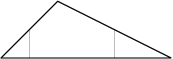
Королевский оружейник, взявшийся за изготовление щита, предложил следующий способ: два имеющихся щита кладутся рядом так, чтобы они соприкасались сторонами и фиксируются в таком положении. Сэр Петрейн заметил, что как бы оружейник не старался, у полученного в результате щита всегда будет одинаковая площадь, а значит его эффективность в бою с драконом будет зависеть только от того, какие щиты дал Петрейн оружейнику, но не от того, как они скреплены.

Но ему нужен не просто кусок металла, а щит с символикой его рода: золотым обрамлением по периметру. Однако золото сейчас дорого, поэтому Петрейну хочется, чтобы периметр полученного щита был как можно меньше. Помогите ему выяснить, какой минимальный периметр может иметь щит.