2390 год. В заброшенном метрополитене города N-ска завелась громадная змея-мутант. Она ползает вдоль перегонов между станциями, повергая в ужас случайно забредающих под землю потомков людей. Размеры змеи настолько велики, что иногда голова появляется на той станции, вдоль которой еще ползет какая-то другая часть тела, и змея повергает в ужас сама себя. Чтобы избавиться от этой проблемы, змея поймала вас и потребовала написать для нее программу, которая может ей прокладывать кратчайший маршрут для головы от одной станции до другой, не проползая при этом по станциям, где находятся участки ее тела.
Будем называть маршрутом последовательность станций, каждые две последовательные из которых соединены перегоном.
Все перегоны в метрополитене имеют одинаковую длину, а змея имеет длину в \((l - 0.5)\) перегонов. Змея может ползти вдоль перегонов, переползая с одного на другой на станциях. Змея может ползти вдоль перегона только в один слой, а ее голова не может появляться на станции, если в этот момент по станции проползает другая часть ее тела. Змея умеет ползать только головой вперед.
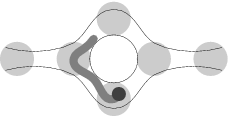
С точки зрения теории графов метрополитен города N-ска является вершинным кактусом. Это означает, что ни одна станция не лежит на двух различных циклических маршрутах и никакие два перегона не соединяют одну и ту же пару станций, никакой перегон не соединяет станцию саму с собой, от каждой станции до любой другой до появления змеи можно было добраться по перегонам.
По заданным карте метрополитена, начальному положению змеи и станции, на которую змея хочет поместить свою голову, выясните, какое минимальное количество перегонов придется проползти змее.
В первой строке ввода записано два числа \(n\) и \(k\) — количество станций и количество перегонов в метрополитене (\(1 \le n, k \le 100\,000\)). В следующих \(k\) строках записано по два различных целых числа \(a\) и \(b\) — номера станций, соединенных соответствующим перегоном.
В следующей строке записано единственное число \(l\), характеризующее длину змеи. В следующей строке записано \(l + 1\) число: номера станций, на которых лежат последовательные части змеи, начиная с головы, а также номер станции, в перегоне к которой лежит хвост змеи длиной в \(0.5\) перегона. Исходно змея расположена таким образом, что ни в каком перегоне не находится одновременно две различных части змеи и змея не пересекает себя ни на какой станции.
В последней строке записано единственное целое число — станция, на которую змея хочет поместить свою голову.
Если змея сможет выполнить свою задачу, выведите длину пути — количество перегонов, через которые необходимо проследовать голове змеи.
Если задача невыполнима, выведите единственное число \(-1\).
У Коли сегодня день рождения! По этому случаю он решил после олимпиады сходить с друзьями в парк аттракционов. И какая удача — можно купить групповой билет сразу на всех, всего за \(S\) рублей!
Конечно, скидываться придется всем поровну. То есть, если Коля позовет \(k\) своих друзей, то каждому придется заплатить \(S/(k + 1)\) рублей (да, сам Коля тоже должен внести свою долю). При этом \(S\) не обязательно должно делиться на \(k + 1\): главное — купить билет, а между собой друзья уж как-нибудь договорятся.
Всего у Коли \(n\) друзей, при этом \(i\)-й из них готов пойти с Колей в парк, если доля, которую ему придется заплатить не больше \(b_i\) (больше денег у него просто с собой нет) и не меньше \(a_i\) (иначе он решит, что Колин день рождения — это скучно, и пойдет играть в волейбол с Сережей).
Так что может так получиться, что всех позвать не удастся. Ну и ладно. Для каждого своего друга Коля знает число \(f_i\) — количество веселья, который тот произведет, если его позвать.
Помогите Коле выбрать подмножество друзей, которых Коля должен позвать с собой, чтобы максимизировать суммарное веселье.
В первой строке входного файлы содержится два целых числа: \(n\) и \(S\) (\(1 \le n \le 100\,000\), \(0 \le S \le 10^9\)) — количество друзей Коли и стоимость билета. В следующих \(n\) строках содержится по три целых числа: в \(i\)-й из этих строк находятся числа \(a_i\), \(b_i\) и \(f_i\) (\(0 \le a_i \le b_i \le S\), \(0 \le f_i \le 10^9\)). Они означают, что \(i\)-го друга можно позвать на вечеринку, если доля, которую ему придется заплатить, лежит между \(a_i\) и \(b_i\), и он произведет \(f_i\) веселья.
В первой строке выходного файла выведите два числа: \(k\) (количество приглашенных на вечеринку друзей) и \(F\) (максимальное суммарное веселье, которое можно получить). Во второй строке выведите \(k\) чисел — номера друзей, которых нужно пригласить.
Когда Петя учился в младших классах, он любил заниматься выпиливанием лобзиком из фанеры различных фигурок. Чтобы можно было заново выпилить наиболее интересные варианты, каждый раз делая распил, он записывал в свою тетрадку, какую фигуру он распилил на какие части.
Недавно Петя нашел у себя в тетрадке запись, из которой следовало, что он распилил n-угольник вдоль прямой, проходящей через две его вершины. В результате распила образовалось ровно две части, одна из которых — k-угольник, а другая — m-угольник. Петя заинтересовался, каким образом такое могло получиться.
Помогите Пете, постройте n-угольник и укажите в нем две различные вершины A и B таким образом, чтобы при распиле n-угольника вдоль прямой AB, получилось ровно два многоугольника, один из которых является k-угольником, а другой — m-угольником.
Входной файл содержит три целых числа: n, m и k (3 ≤ n, m, k ≤ 200).
Если описанная в условии ситуация могла иметь место, выведите на первой строке выходного файла слово «Yes». В этом случае затем следует вывести пример многоугольника и распила. Следующие n строк должны содержать по два целых числа — координаты вершин многоугольника в порядке обхода. Координаты не должны превышать 104 по модулю. Граница многоугольника не должна иметь самопересечений и самокасаний. Никакие три подряд идущие вершины многоугольника не должны лежать на одной прямой.
Будем считать вершины пронумерованными от 1 до n в порядке, в котором они выведены. Последняя строка должна содержать два числа: номера вершин, через которые был проведен распил.
Если описанная в условии ситуация невозможна, выведите на первой строка выходного файла слово «No».
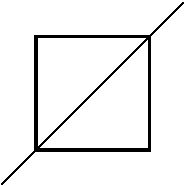
Рисунок ко второму примеру 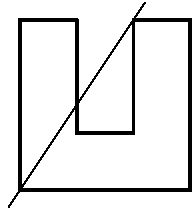
4 3 3
Yes 0 0 1 -4 1000 0 999 4 1 3
8 4 7
Yes 0 0 1 -4 1 -5 999 1 1000 0 999 4 999 5 998 4 1 5
В одной сельской школе решили начать преподавание информатики. Начали с создания кабинета информатики. Так как специального помещения для этих целей в школе нет, то было решено переоборудовать кабинет математики.
Было закуплено n устройств: системные блоки, мониторы, проектор и т. д. Однако, когда начался процесс подключения, неожиданно выяснилось, что в кабинете есть только одна электрическая розетка.
Решение было найдено достаточно быстро — были куплены k сетевых фильтров. После этого выяснилось, что как устройства, так и сетевые фильтры обладают различными характеристиками — это делает процесс подключения нетривиальным. Для каждого сетевого фильтра известно число Ai розеток в нем и максимальная суммарная мощность Bi устройств, которые могут быть в него подключены, а для каждого устройства известна потребляемая им мощность Ci.
Теперь необходимо составить схему подключения устройств с использованием сетевых фильтров такую, что суммарная мощность устройств, включенных в каждый сетевой фильтр (как напрямую, так и через другие сетевые фильтры) не превосходит соответствующего значения Bi, а число устройств и других сетевых фильтров, напрямую включенных в этот, не превосходит Ai. При этом, в соответствии с правилами пожарной безопасности, в каждый сетевой фильтр можно подключать не более одного другого сетевого фильтра.
Можно считать, что единственная в классе розетка рассчитана на достаточно большую мощность — она выдержит подключение всех имеющихся устройств. Отметим также, что при необходимости в розетку можно включить не сетевой фильтр, а устройство напрямую.
Напишите программу, которая найдет требуемую схему подключения устройств.
Первая строка входного файла содержит k — число имеющихся в наличии сетевых фильтров (1 ≤ k ≤ 100 000). Далее следуют k строк, описывающих эти сетевые фильтры: каждая из них содержит по два целых числа: Ai и Bi — количество розеток в нем и максимальную суммарную мощность приборов, которые можно включить в него, соответственно (2 ≤ Ai ≤ 100 000, 1 ≤ Bi ≤ 109).
Следующая строка содержит n — число приборов, которые нужно подключить (1 ≤ n ≤ 100 000). Последняя строка входного файла содержит мощности этих приборов: C1, ..., Cn (1 ≤ Ci ≤ 109).
В выходной файл выведите слово «Yes», если все приборы можно подключить с использованием имеющихся в наличии сетевых фильтров, и слово «No» — в противном случае.
Если ответ на задачу положительный, то далее выведите описание схемы подключения. Оно должно состоять из двух строк. Первая из этих строк должна описывать подключение сетевых фильтров: для каждого из них выведите номер фильтра, в который он подключен (если он подключен в единственную розетку в классе, то выведите число 0, а если он вообще не используется, то число - 1). Вторая из этих строк должна описывать подключение приборов: для каждого из приборов выведите номер сетевого фильтра (если прибор следует подключить непосредственно в розетку, то выведите число 0), в который он подключен.
Учитывайте, что в каждый сетевой фильтр может быть подключен не более чем один другой сетевой фильтр, а подключать фильтр сам к себе не разрешается. Если в сетевой фильтр не включены (напрямую или через другие сетевые фильтры) никакие устройства, то он также не должен быть никуда включен. Кроме этого, если фильтр не включен (напрямую или через другие сетевые фильтры) в розетку, то он также не должен быть никуда включен.
Сетевые фильтры нумеруются, начиная с единицы, в порядке их перечисления во входном файле. Порядок вывода описания подключения фильтров и приборов должен совпадать с порядком их перечисления во входном файле.
2 2 20 2 10 3 10 5 5
Yes 0 1 1 2 2
1 2 10 1 20
Yes -1 0
Сегодня на уроке математики шестиклассник Петя изучил понятие наибольшего общего делителя. Петя тут же решил применить полученные знания на практике.
Петя выписал на листке бумаги \(n\) чисел \(a_1, \ldots, a_n\) --- номера домов, в которых живут его друзья. Теперь он хочет выбрать такое подмножество этих чисел, чтобы их наибольший общий делитель был равен его любимому числу \(d\).
Помогите Пете выбрать из выписанных чисел искомое подмножество.
Первая строка входного файла содержит два целых числа \(n\) и \(d\) (\(1 \le n \le 1000\), \(1 \le d \le 10^9\)). Вторая строка содержит \(n\) целых чисел: \(a_1, a_2, \ldots, a_n\) (\(1 \le a_i \le 10^9\)).
Если существует искомое подмножество, выведите на первой строке выходного файла число \(k\) --- количество чисел в нем. На второй строке выведите числа, входящие в это подмножество.
Если решения не существует, выведите на первой строке выходного файла число \(-1\).
Если возможных ответов несколько, выведите любой из них.
4 3 6 8 12 9
2 6 9
3 3 2 4 8
-1