В Берляндии готовятся к проведению очередного этапа по гонкам машин класса I2011.
Известно, что машины этого класса не могут двигаться со скоростью, превышающей \(v\) м/с, при разгоне мощности двигателя хватает, чтобы развить любое ускорение, не превышающее \(a\) м/с\(^2\), а при торможении абсолютная величина ускорения не превышает \(b\) м/с\(^2\).
Трасса в Берляндии устроена следующим образом. Сначала идет длинная прямая, на которой машины могут разогнаться до любой скорости от 0 до \(v\). Затем следует линия старта, после которой следует отрезок длиной \(x\) м, поворот на 90\(^\circ\) и отрезок длины \(y\) м, после которого находится линия финиша. Линию финиша машина может пересечь на любой скорости.
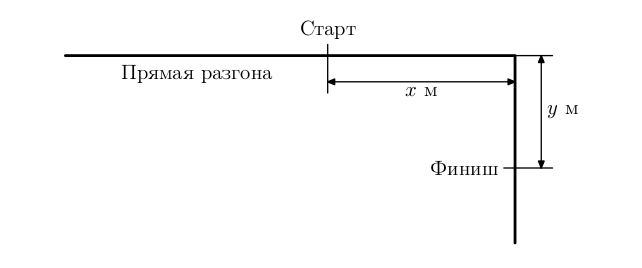
Для прохождения поворота рекомендуется использовать управляемый занос. Для этого необходимо затормозить таким образом, чтобы скорость оказалась равна 0 в точности в повороте. После этого, сделав резкое движение рулем по направлению поворота и резко нажав газ, можно, не теряя времени, уйти на второй отрезок трассы.
Виталий планирует участвовать в соревнованиях. Он решил рассчитать, за какое минимальное время он сможет пройти трассу. Помогите ему это сделать.
Входной файл содержит пять целых чисел: \(v\), \(x\), \(y\), \(a\), \(b\) (\(1 \leq v, x, y, a, b \leq 10^6\)).
Выведите в выходной файл минимальное время, за которое возможно пройти всю трассу. Ваш ответ должен иметь абсолютную или относительную погрешность не больше \(10^{-8}\).
4 10 12 1 2
8.5
В приведенном примере следует действовать так. На прямой разгона следует разогнаться до максимальной возможной скорости в 4 м/с. После старта следует проехать 6 м на максимальной возможной скорости за 1.5 с, затем за 2 с затормозить до 0, используя максимальное возможное торможение, заодно проехав оставшиеся 4 м до поворота. Войдя с заносом в поворот, следует нажать на газ и с максимальным ускорением разогнаться за 4 с до максимальной скорости в 4 м/с, пройдя за это время 8\,м. После этого оставшиеся 4 м до финиша следует пройти за 1 с на максимальной скорости. Общее время на прохождение трассы равно \(1.5+2+4+1=8.5\) с.
Члены жюри Всероссийской командной олимпиады школьников по программированию очень любят пить чай. Но, к сожалению, в их распоряжении всего один чайник, имеющий объем \(v\) мл. Работа жюри хорошо отлажена, поэтому точно известно, кто и когда отправиться пить чай, и сколько воды ему для этого нужно.
Рассмотрим действия, предпринимаемые членами жюри для получения желанного напитка.
Когда человек из жюри подходит к чайнику, то если никого больше у чайника нет, он смотрит, достаточно ли в чайнике воды. Если в чайнике не хватает воды для этого человека, то он доливает в чайник воды до полного объема в \(v\) мл. Если же воды достаточно, то вода в чайник не доливается. После этого чайник включается и доводит воду до температуры 100 градусов. После этого член жюри наливает себе необходимый объем кипятка для заварки чая и отходит от чайника.
Если в момент прихода к чайнику член жюри обнаруживает других людей, ожидающих кипятка, то он становится в очередь и дожидается, пока все предыдущие люди выполнят свои действия с чайником.
Температура кипения воды составляет 100 градусов Цельсия. Мощность чайника составляет \(N\), что означает, что если в чайнике \(x\) мл воды, то температура воды в чайнике изменяется по формуле \(T(t) = T_0 + \frac{Nt}{x}\), где \(T_0\) — температура воды в момент включения чайника, а \(t\)~— время в секундах, прошедшее с момента включения чайника. Когда температура воды достигает 100 градусов, чайник автоматически выключается.
Когда чайник выключен, вода в нем начинает остывать. Вне зависимости от количества жидкости в чайнике, температура воды падает со скоростью \(k\) градусов в секунду. Когда вода достигает комнатной температуры в 20 градусов, остывание прекращается.
Заливаемая в чайник вода имеет комнатную температуру 20 градусов. При доливании воды в чайник температура воды усредняется, а именно, если в чайнике было \(w\) мл воды температуры \(T\), то температура воды в чайнике после его заполнения станет \(\frac{wT + 20(v-w)}{v}\).
Известны времена, когда члены жюри идут пить чай, а также количество кипятка им необходимое. Требуется для каждого члена жюри вывести в какой момент он начнет пить чай. Считается, что разливают воду по чашкам и заваривают чай члены жюри моментально, при этом всегда наливая себе ровно необходимый им объем. Изначально чайник пуст.
Первая строка входного файла содержит четыре целых числа \(m\), \(v\), \(N\) и \(k\) (\(1 \le m \le 100\,000\), \(1 \le v, N, k \le 1000\)) — количество членов жюри, пьющих чай, объем чайника в мл, мощность чайника и скорость остывания воды в чайнике. Далее следуют \(m\) строк — описания людей, пьющих чай. В каждой строке два целых числа \(t_i\) и \(a_i\) (\(1 \le t_i \le 10^6\); \(1 \le a_i \le v\)) — время в секундах от начала олимпиады, когда член жюри отправиться пить чай, и необходимый ему объем воды в мл. Никакие два члена жюри не отправляются пить чай одновременно.
В выходной файл выведите \(m\) строк по одному числу в каждой — время в секундах от начала олимпиады, когда соответствующий член жюри начнет пить чай. Ответ должен иметь абсолютную или относительную погрешность не более \(10^{-7}\).
3 1000 200 1 1 500 501 300 551 300
401.0 701.0 1021.0
Совсем скоро начнется первый тур очередной всероссийской командной олимпиады школьников по палеонтологии (ВКОШП). На олимпиаду приехали команды из \(n\) школ, от каждой школы приехало ровно по две команды. Команды уже заняли свои места, когда обнаружилось, что некоторые команды из одной школы сидят слишком близко. Перед организаторами олимпиады встала серьезная задача — пересадить участников олимпиады.
Столы, за которыми сидят команды, расставлены в один ряд. Расстояние между рабочими местами соседних команд оказалось равно 10 метрам. Организаторы хотят, чтобы минимальное расстояние между двумя командами из одной школы было как можно больше.
Пересаживая команду, организатором необходимо перенести на новое место все оборудование, приготовленное командой для исследований. Поэтому организаторы хотят пересадить команды так, чтобы сумма расстояний между старыми и новыми рабочими местами команд была как можно меньше.
Например, пусть в соревновании принимают участие по две команды школ 1, 2, 3 и 4. Пусть исходно команды распределены по рабочим местам следующим образом: 1, 3, 2, 2, 1, 4, 4, 3 (для каждой команды указан номер школы, которую она представляет). При таком распределении по рабочим местам команды из школы 2 сидят слишком близко, как и команды из школы 4. Пересадив команды в следующем порядке: 1, 3, 2, 4, 1, 3, 2, 4, жюри может добиться своего: команды из одной школы сидят на местах, расстояние между которыми не меньше 40\,м, большего расстояния добиться нельзя. Сумма расстояний между старыми и новыми позициями для данного примера равна \(0 + 0 + 0 + 20 + 0 + 20 + 30 + 10 = 80\)\,м, для исходного распределения команд она минимальна.
Вам задано исходное распределение команд по рабочим местам. Требуется пересадить их так, чтобы минимальное расстояние между командами из одной школы было как можно больше. При этом среди возможных новых размещений команд следует выбрать такое, чтобы сумма расстояний между старыми и новыми местами рабочими команд была минимально возможной.
В первой строке входного файла задано число \(n\) — количество команд (\(1 \le n \le 100\)). Во второй строке задано исходное распределение команд по рабочим местам — последовательность \(a_1, a_2, \ldots, a_{2n}\). Для каждой команды указан номер школы, которую она представляет. Гарантируется, что последовательность состоит из чисел от одного до \(n\) и каждое число встречается ровно два раза.
В единственную строку выходного файла выведите, каким образом следует пересадить команды, чтобы минимальное расстояние между командами из одной школы было как можно больше. При этом среди возможных новых размещений команд следует выбрать такое, чтобы сумма расстояний между старыми и новыми рабочими местами команд была минимально возможной. Если оптимальных ответов несколько, можно вывести любой из них.
4 1 3 2 2 1 4 4 3
1 3 2 4 1 3 2 4
Маленький Вася очень любит поезда. На день рождения ему подарили игрушечную железную дорогу. В комплект к железной дороге входит поезд, состоящий из \(n\) вагонов, пронумерованных числами от 1 до \(n\).
Любимым занятием Васи стала сортировка поездов с использованием специального сортировочного тупика.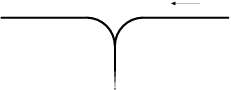
Справа к тупику подъезжает поезд, составленный из всех \(n\) вагонов. Затем вагоны по одному загоняются в сортировочный тупик и выгоняются из него налево. Васе нравится, если ему удается отсортировать поезд с помощью сортировочного тупика — добиться того, чтобы слева от тупика вагоны были расположены по порядку от 1 до \(n\).
Например, пусть в исходном поезде 4 вагона, которые следуют в порядке 3, 1, 2, 4. Его можно отсортировать следующим образом. Загоняем вагон 3 в тупик. Загоняем вагон 1 в тупик. Выгоняем вагон 1 из тупика. Загоняем вагон 2 в тупик. Выгоняем вагон 2 из тупика. Выгоняем вагон 3 из тупика. Загоняем вагон 4 в тупик. Выгоняем вагон 4 из тупика.
Не все поезда можно отсортировать таким образом. Например, поезд из 3 вагонов, следующих в порядке 2, 3, 1, отсортировать нельзя.
Вася выписал на листке в лексикографическом порядке все поезда длины \(n\), которые можно отсортировать с помощью тупика. Поезд \((a_1, a_2, \ldots, a_n)\) идет раньше поезда \((b_1, b_2, \ldots, b_n)\) в лексикографическом порядке, если существует такое \(i\) (\(1 \le i \le n\)), что для всех \(j < i\) выполняется \(a_j = b_j\), а \(a_i < b_i\). Например, все поезда из трех вагонов, которые можно отсортировать с помощью тупика, в лексикографическом порядке выписываются следующим образом: \((1, 2, 3)\), \((1, 3, 2)\), \((2, 1, 3)\), \((3, 1, 2\)), \((3, 2, 1)\).
Вася потерял свой листок, и его интересует вопрос: какой поезд был выписан на его листке под номером \(k\). Помогите ему выяснить это.
Входной файл содержит два целых числа — \(n\) и \(k\) (\(1 \le n \le 30\), \(1 \le k \le 10^{18}\)).
Выведите в выходной файл \(n\) целых чисел: \(k\)-й в лексикографическом порядке поезд из \(n\) вагонов, который можно отсортировать с помощью тупика.
Если с помощью тупика можно отсортировать менее \(k\) поездов из \(n\) вагонов, выведите \(-1\).
4 1
1 2 3 4
4 3
1 3 2 4
4 15
-1
Глеб очень любит историю. Он приходит в полный восторг, когда ему предлагают изучить историю какой-либо конкретной династии. Глеб очень строго относится к чистоте крови, поэтому при анализе династии он включает в рассмотрение только мужчин, которые являются кровными потомками основателя династии по отцовской линии.
Один из главных методов исторического анализа династии — изучение количества сыновей некоторого ее представителя. Глеб же намеревается произвести настоящую революцию в исследованиях — он намерен изучать не просто количество сыновей, а количество внуков, правнуков, праправнуков и так далее. Однако, династии могли тянуться несколько десятков поколений, а значит общее число кровных потомков очень велико, так что Глебу стало очень тяжело работать. Поскольку на дворе сейчас XXI век, Глеб решил обратиться за помощью к квалифицированным программистам.
Династия представляет собой множество людей, один из которых называется основателем династии, а любой другой представитель династии \(U\) имеет отца \(V\), являющегося представителем династии. При этом \(U\) является сыном \(V\), или потомком \(U\) через \(1\) поколение. Потомком \(U\) через \(k+1\) поколение называется сын \(V\) некоторого потомка \(U\) через \(k\) поколений.
Глеба интересует информация о том, сколько у некоторого представителя династии \(V\) существует потомков через \(k\) поколений. Разумеется, Глеба интересует далеко не один такой вопрос.
В первой строке входного файла содержится одно число \(n\) — количество человек в династии, которую исследует Глеб (\(1 \le n \le 10^5\)), представители династии пронумерованы различными натуральными числами от 1 до \(n\). Далее следуют \(n\) чисел, \(i\)-е из которых задает номер отца \(i\)-го представителя династии, или равно \(-1\), если соответствующий представитель является основателем династии.
Гарантируется, что основатель династии ровно один, и что любой упомянутый представитель династии явялется потомком основателя династии.
В следующей строке содержится число \(m\) — количество вопросов, которое интересует Глеба (\(1 \le m \le 10^5\)). Далее следует \(m\) строк, каждая из которых содержит два целых числа \(v\) и \(k\) (\(1 \le v \le n\), \(1 \le k \le 10^9\)) — номер исследоваемого представителя династии и интересущее Глеба число поколений.
Для каждого вопроса выведите одно число — количество потомков через соответсвующее число поколений у заданного представителя династии.
5 -1 1 2 1 4 2 1 2 4 7
2 0