Вова проводит соревнования и тренировки по программированию в своей школе. Для этого он скачал из Интернета много архивов разных соревнований и сборов по программированию. Он разархивировал все, что скачал, на жесткий диск своего компьютера, и теперь не может разобраться в получившемся наборе файлов. Вова хочет понять, сколько описаний соревнований по программированию он скачал.

Пара файлов называется тестом, если они находятся в одном каталоге и имеют полные имена вида «XY» и «XY.a», где «XY» — номер теста (дополненный ведущим нулем, если он меньше десяти). В первом из указанных файлов хранятся входные данные, а во втором — эталонный ответ.

Каталог называется каталогом с тестами, если в нем есть тесты со всеми номерами от \(1\) до \(N\), где \(1 \le N \le 99\), а других файлов нет (но могут быть подкаталоги).

Каталог называется задачей, если в нем есть файл с именем «check» и любым (возможно пустым) расширением и подкаталог «tests», который является каталогом с тестами. В каталоге-задаче помимо этого могут быть другие файлы и подкаталоги.

Каталог называется описанием соревнования, если в нем есть хотя бы один подкаталог, и все его подкаталоги являются задачами.

Задано описание всех файлов, хранящихся на жестком диске Вовиного компьютера. Необходимо найти, сколько описаний соревнований содержится на его жестком диске.

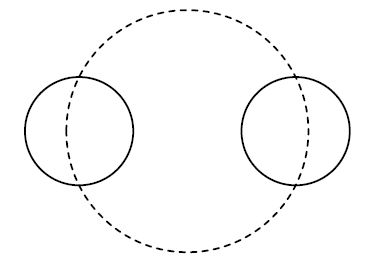
Две страны Байтландия и Флатландия решили объединить свои усилия в исследованиях в области физики высоких энергий и построили \(n\) адронных коллайдеров. Каждый коллайдер имеет форму кольца и находится под землей. При этом можно считать, что толщина каждого из коллайдеров пренебрежимо мала — их можно считать окружностями.

Как известно, адронные коллайдеры — устройства сложные и требующие постоянного внимания. Ни одна из стран не хочет брать на себя обслуживание всех коллайдеров, поэтому было решено поделить обслуживание коллайдеров между странами. Для того чтобы все было честно, было решено, что каждая из стран будет обслуживать ровно половину каждого из коллайдеров. Границу зон ответственности было решено провести в виде окружности. Таким образом, необходимо найти окружность, которая разбивает каждый из коллайдеров на две равные по длине части (то есть пересекает каждый из них в двух диаметрально противоположных точках).

Требуется написать программу, которая по описанию построенных коллайдеров найдет окружность, удовлетворяющую указанным требованиям.

Петя написал свой вариант известной игры «Космические захватчики». Игра состоит в следующем. На землю нападают корабли космических захватчиков. Они выстроены рядами в верхней части экрана. Игрок управляет лазерной пушкой, которая находится у нижнего края экрана в одном из столбцов. За одно действие игрок может передвинуть пушку влево или вправо, либо произвести выстрел вертикально вверх. Если игрок производит выстрел, то он уничтожает ближайший корабль пришельцев в том столбце, в котором находится пушка.

В отличие от оригинальной игры, в Петином варианте корабли пришельцев стоят на месте и не могут стрелять, поэтому игрок не может проиграть. Помогите Пете уничтожить все корабли пришельцев за минимальное число действий.

Дороги Нью-Манхэттена устроены следующим образом. С юга на север через каждые сто метров проходит авеню, с запада на восток через каждые сто метров проходит улица. Авеню и улицы нумеруются целыми числами. Меньшие номера соответствуют западным авеню и южным улицам. Таким образом, можно построить прямоугольную систему координат так, чтобы точка \((x, y)\) лежала на пересечении \(x\)-ой авеню и \(y\)-ой улицы. Легко заметить, что для того, чтобы в Нью-Манхэттене дойти от точки \((x_1, y_1)\) до точки \((x_2, y_2)\) нужно пройти \(|x_2-x_1|+|y_2-y_1|\) кварталов. Эта величина называется манхэттенским расстоянием между точками \((x_1, y_1)\) и \((x_2, y_2)\).

Миша живет в Нью-Манхэттене и каждое утро делает пробежку по городу. Он выбегает из своего дома, который находится в точке \((0, 0)\) и бежит по случайному маршруту. Каждую минуту Миша либо остается на том же перекрестке, что и минуту назад, или перемещается на один квартал в любом направлении. Чтобы не заблудиться Миша берет с собой навигатор, который каждые \(t\) минут говорит Мише, в какой точке он находится. К сожалению, навигатор показывает не точное положение Миши, он может показать любую из точек, манхэттенское расстояние от которых до Миши не превышает \(d\).

Через \(t\cdot n\) минут от начала пробежки, получив \(n\)-е сообщение от навигатора, Миша решил, что пора бежать домой. Для этого он хочет понять, в каких точках он может находиться. Помогите Мише сделать это.

Разбиения числа \(n\) на слагаемые — это набор целых положительных чисел, сумма которых равна \(n\). При этом разбиения, отличающиеся лишь порядком слагаемых, считаются одинаковыми, поэтому можно считать, что слагаемые в разбиении упорядочены по неубыванию.

Например, существует 7 разбиений числа 5 на слагаемые:

В приведенном примере разбиения упорядочены лексикографически — сначала по первому слагаемому в разбиении, затем по второму, и так далее. В этой задаче вам потребуется по заданному разбиению на слагаемые найти следующее в лексикографическом порядке разбиение.