Триангуляцией некоторого набора точек на плоскости называется набор невырожденных треугольников, удовлетворяющий следующим свойствам:
1) Вершинами треугольников являются только точки исходного набора. Каждая точка исходного набора является вершиной хотя бы одного треугольника.
2) Два различных треугольника либо не имеют общих точек, либо имеют общую вершину, либо имеют общую сторону (но площадь их пересечения всегда равна 0).
3) Любая точка, лежащая внутри выпуклой оболочки исходного набора точек, принадлежит хотя бы одному треугольнику (она может принадлежать нескольким треугольникам, если является их общей вершиной или принадлежит их общей стороне). (Выпуклой оболочкой некоторого набора точек называется наименьший выпуклый многоугольник, содержащий все эти точки).
Триангуляция называется триангуляцией Делоне, если кроме того для нее выполняется следующее условие:
Внутри окружности, описанной около любого треугольника из триангуляции, не лежит ни одна из исходных точек (точки могут лежать на окружности, в частности на ней, очевидно, лежат вершины рассматриваемого треугольника).
Для заданного набора точек найдите количество его триангуляций Делоне (две триангуляции считаются различными, если они отличаются хотя бы одним треугольником).
В первой строке вводится число \(N\) - количество точек (3 <= \(N\) <= 30) исходного набора. Следующие \(N\) строк содержат по одной паре вещественных чисел - координаты соответствующей точки. Никакие три точки не лежат на одной прямой.
Выведите количество различных триангуляций Делоне указанного набора точек.
4 0.0 0.0 1.0 0.0 0.0 1.0 1.0 1.0
2
Администрация одного института решила построить в холле фонтан. По плану администрации, фонтан должен иметь форму круга с максимально возможным радиусом. Дизайнеру сообщили, что холл института имеет вид прямоугольника, размером \(X\)×\(Y\) метров. Однако когда дизайнер стал выбирать место для фонтана, он столкнулся с серьезной проблемой: в холле института обнаружилось \(N\) круглых колонн, снести которые не представляется возможным.
Таким образом, у него появилась проблема: где следует поместить фонтан, чтобы он имел максимально возможный радиус и не имел ненулевого по площади пересечения с колоннами. Вам предстоит помочь ему в решении этой нелегкой задачи.
В первой строке входных данных содержатся вещественные числа \(X\) и \(Y\), 1 <= \(X\), \(Y\) <= \(10^4\) . Будем считать, что прямоугольник холла расположен на координатной сетке так, что его углы имеют координаты (0, 0), (\(X\), 0), (\(X\), \(Y\)) и (0, \(Y\)).
Во второй строке задается число \(N\) (0 <= \(N\) <= 10) - количество колонн. Следующие \(N\) строк содержат параметры колонн - \(i\)-я строка содержит три вещественных числа \(X_i\), \(Y_i\) и \(R_i\) - координаты центра и радиус \(i\)-й колонны (\(R_i\) <= \(X_i\) <= \(X\)-\(R_i\), \(R_i\) <= \(Y_i\) <= \(Y\)-\(R_i\), 0.1 <= \(R_i\) <= min(\(X\) / 2, \(Y\) / 2); для любых \(i\) ≠ \(j\) sqrt( (\(X_i\) - \(X_j\))2 + (\(Y_i\) - \(Y_j\))2 )>= \(R_i\) + \(R_j\)). Все вводимые числа разделены пробелами.
Выведите три вещественных числа: \(X_F\), \(Y_F\) и \(R_F\) - координаты центра и радиус фонтана. Фонтан должен быть полностью расположен внутри холла (допускается касание стен) и не иметь ненулевого пересечения ни с одной из колонн (допускается касание). Радиус фонтана должен быть максимален. Разделяйте числа пробелами и/или переводами строки. Если решений несколько, выведите любое из них.
10 10 0
5.000 5.000 5.000
1 1000 0
0.500 0.500 0.500
10 10 4 1 1 1 9 9 1 1 9 1 9 1 1
5.000 5.000 4.657
Власти Флатландии решили построить новый мост через реку Нижний Флат, протекающую с юга на север через территорию страны. В связи с финансовым кризисом средства строителей существенно ограничены, поэтому решено было построить мост минимальной возможной длины. 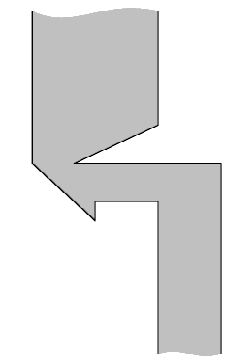
Введем координатную систему таким образом, чтобы ось OY была направлена с юга на север, а ось OX с запада на восток. Берега реки представляют собой ломаные, бесконечные в обе стороны. Левый берег начинается лучом, направленным на юг из точки (x1,1,y1,1), продолжается отрезками (x1,1,y1,1) − (x1,2,y1,2), (x1,2,y1,2)− (x1,3,y1,3), ..., (x1,m−1,y1,m−1) − (x1,m,y1,m) и заканчивается лучом, направленным на север из точки (x1,m,y,m).
Аналогично, правый берег реки начинается лучом, направленным на юг из точки (x2,1,y2,1), продолжается отрезками (x2,1,y2,1) − (x2,2,y2,2), (x2,2,y2,2) − (x2,3,y2,3), ..., (x2,n−1,y2,n−1) − (x2,n,y2,n) и заканчивается лучом, направленным на север из точки (x2,n,y2).
Помогите руководству Флатландии выяснить, мост какой минимальной длины можно построить.
Первая строка входного файла содержит целое число m (2 ≤ m ≤ 100). Следующие m строк содержат по два целых числа координаты вершин ломаной левого берега: x1,1, y1,1, x1,2,y1,2, ...,x1,m, y1,m.
Следующая строка входного файла содержит целое число n (2 ≤ n ≤ 100). Следующие n строк содержат по два целых числа координаты вершин ломаной правого берега: x2,1, y2,1, x2,2, y2,2, ..., x2,n, y2,n.
Известно, что x1,1 < x2,1, каждая из ломаных не имеет самопересечений и самокасаний, ломаные не имеют общих точек. Все отрезки каждой из ломаных имеют положительную длину. Все координаты не превосходят 104 по абсолютной величине
Выведите в выходной файл одно вещественное число: минимальную возможную длину моста. Ваш ответ будет проверяться с точностью 10−5.
Оптимальное положение моста показано на следующем рисунке:
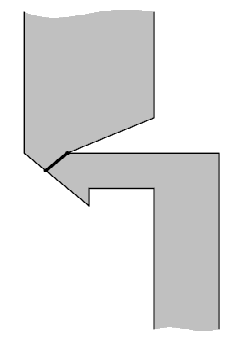
4 6 1 3 1 3 0 0 3 3 9 3 2 3 6 5
1.4142135623730951
Новый мэр крупного города Флатбурга Иван Котянин начал свою работу с решения проблем с пробками в городе. Как и в любом крупном городе, во Флатбурге есть кольцевая автодорога. Во Флатбурге она представляет собой монотонный многоугольник. Монотонным называется многоугольник, с которым каждая прямая, проходящая строго с севера на юг, имеет не более двух общих точек.
После совещания с правительством города было принято решение построить новую магистраль — скоростной диаметр, который вел бы строго с севера на юг и соединял две точки кольцевой автодороги.
Помимо борьбы с пробками решено было обновить рекорд по протяженности самой длинной магистрали, проложенной с севера на юг. Для того чтобы обновить рекорд необходимо построить магистраль длиной хотя бы \(d\) километров, а поскольку лишних денег в бюджете Флатбурга не так уж и много, решено было построить дорогу длиной ровно \(d\).
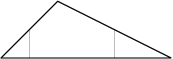
Министр транспорта Флатбурга решил предоставить мэру все варианты строительства новой дороги. Для начала он решил подсчитать, сколько существует способов построить магистраль. Помогите министру.
Первая строка входного файла содержит два целых числа \(n\) — количество вершин у многоугольника, задающего кольцевую автодорогу (\(3 \le n \le 100000\)), и \(d\) — длину новой магистрали (\(1 \le d \le 10^8\)).
Далее следует описание расположения вершин — каждая из следующих \(n\) строк содержит координаты \(x\) и \(y\) (\(-10^8 \le x, y \le 10^8\)) соответствующей вершины. Вершины заданы в порядке их обхода против часовой стрелки.
Направлению с севера на юг соответствуют прямые, задаваемые уравнением \(x = c\) для некоторого \(c\). Заданный многоугольник является монотонным.
В выходной файл выведите количество способов построить дополнительную
магистраль длиной ровно \(d\). Если способов постройки бесконечно много,
выведите в выходной файл «Infinity».