Темы
    Информатика(2656 задач)
---> 10 задач <---
Источники --> Личные олимпиады --> Baltic Olympiad in Informatics
    Baltic Olympiad in Informatics 2018(1 задач)
    Baltic Olympiad in Informatics 2017(0 задач)
    Baltic Olympiad in Informatics 2016(6 задач)
    Baltic Olympiad in Informatics 2015(0 задач)
    Baltic Olympiad in Informatics 2014(2 задач)
    Baltic Olympiad in Informatics 2013(1 задач)
Страница: << 1 2 Отображать по:
#113520
Лабиринт
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes

Уолеви разработал игру, в которой игрок собирает монеты в лабиринте. На данный момент проблема в том, что игра слишком проста. Могли бы вы создать несколько сложных лабиринтов для игры? Каждый лабиринт представляет собой прямоугольную сетку, состоящую из полов (.) И стен (#). Одна из ячеек является базой (x), а некоторые ячейки могут содержать монеты (0). Игрок начинает в базе и может перемещаться влево, вправо, вверх и вниз. Задача игрока - собрать все монеты в лабиринте, а затем вернуться на базу. Трудность лабиринта - это длина кратчайшего пути, который начинается на базе, собирает все монеты и возвращается на базу.

Входные данные

Ввод начинается с целого числа t: количество лабиринтов. После этого следуют t строк. Каждая такая строка содержит три целых числа n, m и k. Это означает, что размер лабиринта должен быть n * m ячеeк, и должно быть ровно k монет.

Выходные данные

Выход должен содержать описания лабиринта, разделенные пустыми строками, в том же порядке, что и на входе. Каждый лабиринт должен быть разрешен.

Входные данные
2
3 3 1
4 7 2
Выходные данные
###
#.x
#o#

.o.####
.#..x.#
...##.#
###o...
Примечание

Трудность первого лабиринта - 4, а трудность второго лабиринта - 18.

Это задача только для вывода, и есть только один входной файл . Вы можете скачать входной файл здесь. Вы должны представить выходной файл, содержащий все лабиринты, указанные во входном файле.

Для каждого лабиринта ваш счет max(0, 100 - 3(d - x)) - где x трудность вашего лабиринта и d сложность самого сложного лабиринта, найденного жюри. Ваш общий балл для задания - это среднее значение всех оценок, округленное до целого.

#114062
Двусторонний ток
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes

Фредерик играет с игрушечной железной дорогой, которую он сам сделал, чем очень гордится. Дорога состоит из \(\)\(N\)\(\) сегментов путей, соединённых по кругу, и пронумерованных \(\)\(1,2,\dots,N\)\(\) по часовой стрелке. Электричество подается локомотиву через M проводов, проложенных арками вдоль круга. Через каждый сегмент дороги проложен как минимум один провод.

Фредерику поднадоел наворачивающий круги поезд, и он решил добавить к каждому сегменту стрелочную развилку, чтобы устраивать поезду аварии и прочим образом злобно развлекаться. Стрелочные развилки, однако, нужно запитать электричеством, причем им подходит только специальный, двусторонний ток.

По каждому проводу, проложенному вдоль путей, ток может течь в одном направлении – либо по часовой, либо против часовой стрелки, причем Фредерик может выбирать направление на своё усмотрение. Двусторонний ток можно получить, если подвести к сегменту ток и в одном, и в другом направлении (по двум разным проводам).

Таким образом, Фредерику нужно придумать, в какую сторону направить ток по каждому проводу, чтобы каждый сегмент путей был бы покрыт как минимум одним проводом с током, текущим по часовой стрелке, и одним проводом с током, текущим против часовой стрелки. Помоги Фредерику решить эту задачу.

Входные данные

На первой строке даны два целых числа \(\)\(N\)\(\) и \(\)\(M\)\(\) – количество сегментов железной дороги и количество проводов, соответственно.

На каждой из следующих \(\)\(M\)\(\) строк даны два числа \(\)\(1 \le a, b \le N\)\(\), указывающих, что имеется провод, покрывающий сегменты \(\)\(a, a+1, \dots , b\)\(\). Если \(\)\(b\)\(\) меньше \(\)\(a\)\(\), это значит что последовательность сегментов перескакивает через \(\)\(N\)\(\), т.е. покрываются \(\)\(a, \dots , N, 1, \dots , b\)\(\). \(\)\(a=b\)\(\), то провод покрывает только один сегмент.

Выходные данные

На единственной строке вывести последовательность символов длиной \(\)\(M\)\(\), состоящую из знаков 0 или 1. \(\)\(i\)\(\)-тый символ должен быть равен 0, если ток в \(\)\(i\)\(\)-том проводе нужно направить по часовой стрелке, и 1, если ток нужно направить против часовой стрелки. Если существует несколько решений, вывести любое из них. Если решений нет, вывести текст "impossible".

Система оценки

Тесты разделены на группы. Очки за группу даются только если корректно решены все тесты в группе.

Группа Очки Ограничения Дополнительные ограничения

1. [13] \(\)\(2\leq N,M\leq 15\)\(\)

2. [20] \(\)\(2\leq N,M\leq 100\)\(\)

3. [22] \(\)\(2\leq N,M\leq 1000\)\(\)

4. [19] \(\)\(2\leq N,M\leq 100000\)\(\) Нет проводов с b<a.

5. [26] \(\)\(2\leq N,M\leq 100000\)\(\)

Примеры
Входные данные
10 5
1 5
6 7
5 1
7 2
2 4
Выходные данные
00101
Входные данные
10 5
1 4
2 5
4 7
6 10
8 1
Выходные данные
impossible
Входные данные
5 2
1 5
3 3
Выходные данные
impossible
Входные данные
5 3
3 3
2 1
4 2
Выходные данные
101
#114085
Три друга
  
ограничение по времени на тест
0.5 second;
ограничение по памяти на тест
256 megabytes

Три друга любят играть в следующую игру. Первый друг выбирает строку \(S\). Затем второй друг создает новую строку \(T\), который состоит из двух копий строки \(S\). Наконец, третий друг вставляет одну букву в начале, в конце или где-то внутри строки \(T\), тем самым создавая новую строку \(U\).

Дана строка \(U\), ваша задача – восстановить исходную строку \(S\).

Входные данные

Первая строка ввода содержит \(N\) (\(2 \leq N \leq 2\,000\,001\)) – длину итоговой строки \(U\). Сама строка \(U\) задается на второй строке. Она состоит из \(N\) заглавных английских букв.

Выходные данные

Ваша программа должна напечатать исходную строку \(S\). Однако есть два исключения:

  1. Если конечная строка \(U\) не могла быть создана с помощью вышеуказанной процедуры, необходимо вывести NOT POSSIBLE .

  2. Если исходная строка \(S\) определяется неоднозначно, следует напечатать NOT UNIQUE .

Система оценки

Решения, правильно работающие на тестах, в которых \(2 \leq N \leq 2001\) будут оцениваться в \(35\) баллов.

Примеры
Входные данные
7
ABXCABC
Выходные данные
ABC
Входные данные
9
ABABABABA
Выходные данные
NOT UNIQUE
Входные данные
6
ABCDEF
Выходные данные
NOT POSSIBLE
#114086
Шаровая машина
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes

У нас есть «шаровая машина», которую можно представить как корневое дерево. Узлы дерева пронумерованы от \(1\) до \(N\). каждый узел либо пуст, либо содержит один шар. Изначально все узлы пусты. В то время работы, машина может выполнить 2 разные операций:

  1. Добавить \(K\) шаров машину: шарики добавляются по одному в узел корня. Если у шара есть пустой узел прямо под ним, он будет скатываться вниз. Если имеется несколько пустых дочерних узлов, шар выберет узел с наименьшим числом в его поддереве. Если же мяч скатывается вниз на несколько уровней, он делает выбор на каждом уровне. Например: если мы добавим два шарики к машине на картинке ниже, они пойдут к узлам \(1\) и \(3\): первый шарик из узла \(4\) к узлу \(3\), потому что узел \(3\) пуст и содержит узел \(1\) в своем поддереве (которое состоит узлов \(3\) и \(1\)); он далее катится от узла \(3\) к узлу \(1\). Второй шарик катится от узла 4 к узлу \(3\) останавливается там.

  2. Удалить шар из указанного узла: этот узел становится пустым и шары сверху (если таковые есть) скатываются вниз. Всякий раз, когда родитель пустого узла содержит шар, этот шар будет скатываться вниз. Если удалить шарики из узлов \(5\), \(7\) и \(8\) (именно в этом порядке) из машины на рисунке ниже, узлы \(1\), \(2\) и \(3\) станут пустыми.

Входные данные

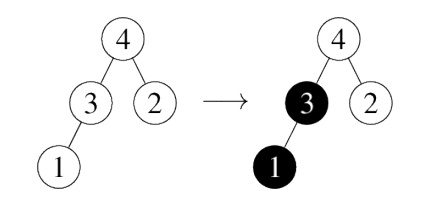
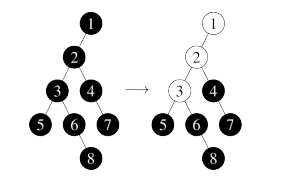
Первая строка содержит два целых числа \(N\) и \(Q\) (\(1 \leq N, Q \leq 100\,000\)) – количество узлов дерева и количество операций соответственно. Следующие \(N\) строк описывают шаровую машину. Каждая из этих строк содержит одно целое число, номер узла: \(i\)-я из этих строк содержит номер родительского узла вершины \(i\) или \(0\), если узел \(i\) является корнем дерева. Каждая из следующих \(Q\) строк содержит по два целых числа и описывает операцию, которую необходимо выполнить. Операция типа \(1\) обозначается \(1 k\) , где \(k\)-количество шариков, добавляемых в машину. Операция типа \(2\) обозначается \(2 x\) , где \(x\)-номер узла, из которого должен быть удален шар. Гарантируется, что все выполняемые операции верны: операции не требуют добавления большего количества шаров, чем есть пустые узлы в шаровой машине, или удаления шара из пустого узла.

Выходные данные

Для каждой операции типа \(1\) выведите номер узла, в котором оказался последний вставленный шар. Для каждой операции типа \(2\) выведите количество шариков, которые скатились вниз после удаления шарика из указанного узла.

Система оценки

Подзадача 1 (25 баллов): каждый узел имеет 0 или 2 дочерних элемента. Кроме того, все узлы с 0 дети находятся на одинаковом расстоянии от корня.

Подзадача 2 (25 баллов): операции будут запрошены таким образом, что никакие шары никогда не скатываются после операции типа 2.

Подзадача 3 (25 баллов): есть ровно одна операция типа 1, и это самая первая операция.

Подзадача 4 (25 баллов): нет доп. ограничений.

Примеры
Входные данные
8 4
0
1
2
2
3
3
4
6
1 8
2 5
2 7
2 8
Выходные данные
1
3
2
2
#114087
Демаркация
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes

Долгое время на острове Байтопия правил справедливый король Байтазар. Но после внезапной смерти царя двое его сыновей-близнецов Битеон и Байтеон не смогли прийти к соглашению, кто из них должен взойти на трон. Поэтому они решили разделить остров на две провинции, чтобы управлять ими самостоятельно. На прямоугольной карте Байтопия имеет форму многоугольника из N вершин.

Каждая сторона многоугольника параллельна одной из сторон карты, а любые две соседние стороны перпендикулярны друг другу. Ни одна из сторон многоугольника не пересекает и не касается любой другой стороны, за исключением общей вершины двух последовательных сторон.

Битеон и Байтеон хотят разделить многоугольник на два конгруэнтных многоугольника, используя один отрезок, содержащийся в полигоне и параллельный одной из сторон карты. (Два многоугольника называются конгруэнтными, если один может быть совмещён с другим с помощью комбинации отражений, поворотов и параллельных переносов). Координаты вершин многоугольника и точки разделяющего отрезка – целые числа.

Сыновья короля просили Вас проверить, возможно ли провести такое разделение.

По данной форме острова, определите, может ли он быть разделен горизонтальным или вертикальным отрезком на две конгруэнтные части. Если это возможно, найдите любой такой отрезок.

Входные данные

Первая строка входных данных содержит одно целое число \(N\) (\(4 \leq N \leq 100\,000\)) – количество вершин. Следующие N\( \)строк содержат по паре целых чисел \(X_i\) и \(Y_i\) (\(0 \leq X_i, Y_i \leq 10^9\)) – координаты \(i\)-й вершины.

Вершины задаются в порядке обхода многоугольника, т. е. отрезки \((X_1, Y_1) - (X_2, Y_2)\), \((X_2, Y_2) - (X_3, Y_3)\), \(\dots\), \((X_{N-1} , Y_{N-1}) - (X_N , Y_N)\) и \((X_N, Y_N) - (X_1, Y_1)\) – все стороны многоугольника. Кроме того, любые два последовательных отрезка перпендикулярны друг другу.

Выходные данные

Ваша программа должна вывести одну строку. Если можно разделить остров на две конгруэнтные части горизонтальным или вертикальным отрезком с конечными точками \((x_1, y_1)\) и \((x_2, y_2)\), выведите \(4\) целых числа \(x_1\), \(y_1\), \(x_2\) и \(y_2\), разделенные пробелами. При этом должно выполняться либо \(x_1 = x_2\), либо \(y_1 = y_2\). Отрезок должен лежать внутри многоугольника и только его конечные точки должны лежать на границе.

Если существует вертикальный разрез – выведите его, иначе выведите горизонтальный. Выводить необходимо отрезок слева направо, либо снизу вверх. Если не удается найти подходящее деление, выведите одно слово NO.

Система оценки

Подзадача 5 (12 баллов). Площадь многоугольника не превосходит 1000.

Подзадача 2 (9 баллов). \(4 \leq N \leq 10 000\). Любая горизонтальная или вертикальная линия, разделяющая многоугольник, делит его ровно на две части.

Подзадача 3 (12 баллов). \(4 \leq N \leq 200\).

Подзадача 4 (20 балла). \(4 \leq N \leq 2 000\).

Подзадача 5 (47 баллов). \(4 \leq N \leq 100 000\).

Примеры
Входные данные
10
0 0
1 0
1 1
3 1
3 5
2 5
2 3
1 3
1 2
0 2
Выходные данные
1 2 3 2
Входные данные
6
0 0
1 0
1 1
2 1
2 2
0 2
Выходные данные
NO
Страница: << 1 2 Отображать по:
Выбрано
:
Отменить
|
Добавить в контест