Теория вероятностей(3 задач)
Конструктив(21 задач)
Формула(17 задач)
Комбинаторика(9 задач)
Мирко нужно купить землю, чтобы построить дом для своей семьи. Он присмотрел K участков. Для простоты будем считать, что участок представляет собой поле с N строками и M столбцами, N × M клеток в сумме.
Мирко знал, что до начала строительства участок надо поддерживать в порядке. По этой причине он приобрёл газонокосилку. Для покоса участка ему нужно проехать по каждой клетке поля хотя бы раз. Он может начать с любой клетки, смотря в одно из четырёх основных направлений (вверх, вниз, влево или вправо). Его газонокосилка может двигаться только вперёд (перемещаться в следующую клетку вдоль текущего направления) или поворачиваться на 90 градусов. К тому же, ради безопасности, Мирко может косить только на своём участке, не выходя за пределы поля.
Так как поворачивать газонокосилку непросто, Мирко хочет минимизировать количество поворотов газонокосилки. Для каждого из K участков земли ему нужно знать минимальное число поворотов для покоса. Помогите Мирко с этой задачей.
В первой строке вводится натуральное число K ( 1 ≤ K ≤ 50 000 ) — число запросов. В каждой из следующих K строк вводятся два натуральных числа N и M ( 1 ≤ N , M ≤ 10 6 ) — размеры поля для каждого запроса.
Для каждого запроса в отдельной стоке выведите минимальное число поворотов газонокосилки, которое потребуется для покоса участка.
Программы, верно работающие на тестах, в которых K = 1 , 1 ≤ N , M ≤ 500 , оцениваются в 50 баллов.
В первом примере первый участок можно покосить без поворотов, если Мирко встанет в первой клетке поля и пойдёт вперёд. Аналогичная идея относится и ко второму участку.
2 1 10 10 1
0 0
3 1 1 3 3 3 4
0 4 4
2 5 8 6 4
8 6
Как известно, в июне во Флатландии будет проходить чемпионат Юпитера по футболу. В турнире примут участие n команд, а сам турнир будет разыгран в один круг, в ходе которого каждая команда сыграет с каждой другой командой.
На Юпитере выпускают футбольную форму m цветов. Каждая команда привезёт с собой два комплекта формы различных цветов. Разумеется, во время матча все игроки одной команды должны быть одеты в форму одного цвета, отличного от цвета формы другой команды.
Для судейства всех матчей этого чемпионата был приглашён глава Фантастической Инопланетной Футбольной Ассоциации Йозеф. Перед началом матча Йозеф назначает каждой из команд цвет футболок, в которых игроки выйдут на поле. Разумеется, выбирать можно только из тех двух цветов футболок, которые привезла с собой команда. После этого Йозеф выбирает себе футболку какого-то цвета, отличного от обоих цветов, в которых будут играть команды. Таким образом, обе команды и судья будут находиться на поле в футболках разного цвета. Любую футболку и команды, и Йозеф могут использовать в неограниченном количестве игр чемпионата.
Футболки для судейства Йозеф закупает непосредственно перед чемпионатом, опираясь на знание о цветах футболок, привезённых командами на турнир. Поскольку Йозеф экономит деньги своей федерации, он хочет купить себе минимальное количество футболок, такое что их хватит для обслуживания всех матчей. Данная задача слишком сложна для обычного футбольного судьи, поэтому он обратился за помощью к вам.
В первой строке входных данных записаны два числа n и m ( 2 ≤ n ≤ 100 000, 2 ≤ m ≤ 10 9 ) — количество команд, участвующих в чемпионате, и количество возможных цветов футболок.
В i -й из следующих n строк записаны два различных целых числа от 1 до m — цвета футболок, которые привезла с собой команда с номером i .
В первой строке выведите минимальное количество футболок, которого хватит Йозефу, чтобы обслужить встречи всех пар команд. Если решения не существует, то выведите одну строку содержащую -1 .
В следующей строке выведите цвета этих футболок.
Если оптимальных решений несколько, разрешается вывести любое из них.
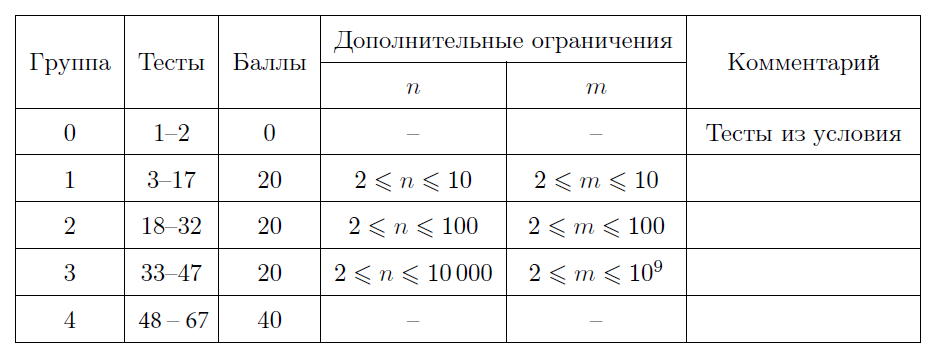
Тесты к этой задаче состоят из пяти групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.
3 4 1 2 2 3 1 4
1 1
5 3 1 2 2 3 2 3 3 1 1 2
2 3 1
Хранители в опасности, и Доктор Манхэттен со своим другом Дэниелом Драйбергом должны срочно их предупредить. Всего в команде хранителей n человек, i -й из которых находится в точке плоскости с координатами ( x i , y i ) .
Как всем известно, доктор Манхэттен вычисляет расстояние между двумя хранителями
i
и
j
по формуле
|
x
i
-
x
j
| + |
y
i
-
y
j
|
. Дэниел, как обычный человек, считает, что расстояние равно
 .
.
Сейчас успех операции зависит от того, сколько существует пар ( i , j ) ( 1 ≤ i < j ≤ n ), таких что расстояние между хранителем i и хранителем j , вычисленное Доктором Манхэттеном, равняется расстоянию между ними, вычисленному Дэниелом. Вычислить эту величину попросили именно вас.
В первой строке входных данных записано число n ( 1 ≤ n ≤ 200 000 ) — количество хранителей.
В каждой из следующих n строк записаны два целых числа x i и y i ( | x i |, | y i | ≤ 10 9 ).
Выведите количество пар хранителей, таких что расстояние между ними, вычисленное доктором Манхэттеном, равно расстоянию, вычисленному Дэниелом.
Тесты к этой задаче состоят из трёх групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.

В первом примере расстояние между хранителем
1
и хранителем
2
равняется
|1 - 7| + |1 - 5| = 10
в понимании Доктора Манхэттена и
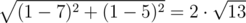 в понимании Дэниела. Для пар
(1, 1)
,
(1, 5)
и
(7, 5)
,
(1, 5)
расстояния, вычисленные Доктором Манхэттеном и Дэниелом, совпадают.
в понимании Дэниела. Для пар
(1, 1)
,
(1, 5)
и
(7, 5)
,
(1, 5)
расстояния, вычисленные Доктором Манхэттеном и Дэниелом, совпадают.
3 1 1 7 5 1 5
2
6 0 0 0 1 0 2 -1 1 0 1 1 1
11
Олег пришел посмотреть на зеркальный лабиринт. Зеркальный лабиринт представляет собой комнату \(n\) на \(n\), у которой каждая клетка или пуста, или содержит зеркало, соединяющее диагональные концы соответствующей клетки. Зеркала в таком лабиринте обладают почти идеальной способностью отражать свет, что создаёт интересные визуальные ощущения и способствует потери ориентации в пространстве.
Олег по натуре очень любопытен, поэтому он решил установить на южной стороне лабиринта \(n\) лазеров, направленных внутрь лабиринта. На северной стороне лабиринта Олег установил \(n\) приёмников, тоже направленных внутрь лабиринта. Пронумеруем лазеры и приёмники с запада на восток от \(1\) до \(n\). Для каждого лазера известен номер приёмника, в который он должен попасть. Так как в один приёмник не могут попасть одновременно два лазера, то эти номера образуют перестановку — каждый из номеров приёмников встречается ровно один раз.
Вы пришли в лабиринт вместе с Олегом. Помогите ему расставить зеркала в изначально пустом лабиринте так, чтобы максимальное количество лазеров попали туда, куда они должны. За пределами лабиринта зеркал нет, так что если лазерный луч покидает пределы лабиринта, то он не сможет вернуться назад.
Первая строка содержит одно целое число \(n\) (\(1 \le n \le 1000\)) — размеры лабиринта.
Во второй строке дана перестановка из \(n\) целых чисел \(a_i\) (\(1 \le a_i \le n\)), где \(a_i\) задаёт номер приёмника, в который должен попасть \(i\)-й лазер.
В первой строке выведите наибольшее возможное количество попавших лазеров.
В следующих \(n\) строчках длины \(n\) выведите расстановку зеркал, приводящую к такому количеству попавших лазеров. Если соответствующая клетка пуста, то выведите « . », иначе выведите « / » или « \ », в зависимости от ориентации зеркала.
В выводе север должен находиться сверху, юг — снизу, а запад и восток — слева и справа соответственно.
Допускается, что некоторые лазеры могут попасть не в свои приёмники, но они не учитываются в подсчёте числа попавших лазеров.
Если существует несколько расстановок зеркал, приводящих к оптимальному ответу — выведите любую из них.
Картинка иллюстрирует расстановку зеркал из первого примера.

4 4 1 3 2
3 .\.. \\.. /../ ...\
Назовём палиндромом непустую строку, которая читается одинаково справа налево и слева направо. Например, « abcba », « a » и « abba » являются палиндромами, а « abab » и « xy » не являются.
Назовём подстрокой строки строку, полученную отбрасыванием некоторого (возможно, нулевого) количества символов с начала и с конца строки. Например, « abc », « ab » и « c » являются подстроками строки « abc », а « ac » и « d » не являются.
Назовем палиндромностью строки количество её подстрок, которые являются палиндромами. Например, палиндромность строки « aaa » равна \(6\), так как все её подстроки являются палиндромами, а палиндромность строки « abc » равна \(3\), так как только подстроки длины \(1\) являются палиндромами.
Вам дана строка \(s\). Вы можете произвольным образом переставлять символы в ней. Требуется получить строку, имеющую максимальную палиндромность.
В первой строке задано целое число \(n\) (\(1 \le n \le 100\,000\)) — длина строки \(s\).
Во второй строке задана строка \(s\), состоящая из \(n\) строчных букв латинского алфавита.
Выведите строку \(t\), которая состоит из тех же символов (с учётом кратностей), что и \(s\), и имеет максимальную палиндромность среди всех строк, которые могут быть получены из \(s\) перестановкой символов.
Если подходящих строк несколько, выведите любую.
В первом примере у строки « ololo » есть \(9\) подстрок-палиндромов: « o », « l », « o », « l », « o », « olo », « lol », « olo », « ololo ». Обратите внимание, что некоторые подстроки совпадают, но учитываются несколько раз.
Во втором примере палиндромность строки « abccbaghghghgdfd » равна \(29\).
5 oolol
ololo
16 gagadbcgghhchbdf
abccbaghghghgdfd