Темы --> Информатика --> Другое
    Разбор случаев(6 задач)
    Теория вероятностей(3 задач)
    Конструктив(21 задач)
    Формула(17 задач)
    Комбинаторика(9 задач)
---> 54 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 1 2 3 4 5 6 7 >> Отображать по:
#990
Праздники
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Нерабочими называются выходные, а также праздники: 23 февраля, 8 марта и K первых дней года. Праздник попавшие на выходные, переносятся. По заданному K требуется определить максимальное количество подряд идущих нерабочих дней.

Парламент некоторой страны принял новый закон о праздничных днях. Согласно этому закону первые K дней года, а также 23 февраля (День олимпиады по информатике) и 8 марта объявляются праздничными, а все остальные праздники отменяются. При этом все выходные (суббота и воскресенье), попавшие на праздничные дни, переносятся на следующие за этими праздниками рабочие дни.

В зависимости от того, на какой день недели приходится 1 января, количество нерабочих дней, которые идут подряд, может меняться.

Требуется определить, какое наибольшее количество нерабочих дней может идти подряд.

Входные данные

На вход подается единственное число K (1≤K≤50).

Выходные данные

Требуется вывести единственное число — наибольшее количество нерабочих дней, идущих подряд.

Примеры
Входные данные
2
Выходные данные
4
Входные данные
10
Выходные данные
16
#1039
Магия Копперфильда
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Дана прямоугольная таблица. Фишка в таблице может перемещаться в любое место на K ходов. Требуется последовательно убрать все ячейки таблицы, кроме одной, задавая количество ходов, на которые должна сходить фишка, и координаты удаляемых клеток. Фишка должна оказаться в единственной оставшейся клетке.

Всемирно известный маг Дэвид Копперфильд любит показывать следующий трюк. Квадрат из N столбцов и N строк, в каждой клетке которого находится какая-нибудь картинка, появляется на экране телевизора. Пусть все картинки пронумерованы следующим образом:

1

2

…

N

N+1

N+2

…

2*N

:

:

…

:

N*(N–1)+1

N*(N–1)+2

…

N*N

Дэвид просит каждого зрителя поставить палец на левую верхнюю картинку (то есть в клетку номер 1), и Магия начинается: маг просит зрителей сдвинуть свой палец K1 раз в произвольном направлении (сдвигать палец разрешается только на соседнюю картинку по горизонтали или по вертикали, оставлять палец на месте запрещено, при этом если, допустим, Дэвид попросил сдвинуть палец 3 раза, то можно, например, сдвинуть палец на одну клетку вправо, затем — на одну клетку вниз, затем — на одну вверх). Затем со словами "Ваш палец не здесь" Дэвид убирает некоторые картинки, и — что удивительно, пальцы телезрителей действительно не указывают на те картинки, которые убирает Дэвид. Затем он просит сделать K2 ходов, и так далее (если Дэвид уже убрал какую-то картинку, то ходить через эту клетку нельзя). В конце, Дэвид убирает все картинки, кроме одной, и, улыбаясь, говорит: "Вы здесь" (аплодисменты).

Дэвиду приходится довольно часто повторять этот трюк, и, чтобы не ошибиться, он попросил написать программу, которая будет ему сообщать, сколько ходов должны делать телезрители, и какие картинки нужно убирать. Напишите такую программу.

Входные данные

Во входном файле записано одно число N — размер квадрата (2N100).

Выходные данные

В выходной файл ваша программа должна печатать следующие строки чисел:

K1 X1,1 X1,2 … X1,m1

K2 X2,1 X2,2 … X2,m2

…

Ke Xe,1 Xe,2 … Xe,me

где Ki — это число ходов, которые должны сделать телезрители, а Xi,1 … Xi,mi — номера картинок, которые Дэвид должен убрать с экрана после этого. При этом все Ki должны удовлетворять условию 2NKi10000 и все Ki должны быть различны. Каждая картинка (кроме той, которая останется) должна убираться ровно один раз. После каждой просьбы зрителей сделать Ki ходов, Дэвид должен убирать хотя бы одну картинку. Каждое Ki должно печататься в начале новой строки. Ситуаций, когда телезритель остался на клетке, у которой нет соседних, а его просят куда-нибудь ходить, возникать не должно.

Примеры
Входные данные
3
Выходные данные
7 1 3 7 9
9 2 4 6 8
#1107
Лягушачьи игры
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Имя входного файла: frogs.in
Имя выходного файла: frogs.out

В тридесятом царстве в новогодние праздники все лягушки собираются на самом большом болоте, чтобы поиграть в замечательную игру. Всего в этом царстве живет N зеленых лягушек и M коричневых. Для игры они выбирают на болоте N + M + 1 кочку, на первые N кочек слева садятся зеленые лягушки, а на последние M — коричневые (т. е. между ними находится одна кочка, на которой никто не сидит). Зеленые лягушки садятся лицом к коричневым лягушкам, а коричневые — к зеленым. Кочки настолько маленькие, что развернуться на них, не свалившись в болото, совершенно не возможно. Поэтому лягушки могут двигаться только вперед и не могут разворачиваться.

На каждом ходе игры одна из лягушек перепрыгивает с той кочки, где она сидит, на свободную кочку. При этом лягушка может прыгнуть на соседнюю кочку вперед, либо перепрыгнуть через одну кочку, если соседняя занята.

Чтобы праздник удался, зеленые лягушки должны оказаться на последних кочках, а коричневые — на первых. Порядок, в котором лягушки окажутся на кочках, не важен. Так как на праздник каждый раз приходит разное количество лягушек, то им каждый год приходится придумывать очередность прыжков. Напишите программу, которая поможет лягушкам составить план прыжков.

Поиграть в эту игру для случая N=M=3 можно по ссылке:

http://olympiads.ru/zaoch/2007/problems/frogs.swf

Входные данные

Во входном файле записаны два числа N и M (1≤N≤1000, 1≤M≤1000) – количество зеленых и коричневых лягушек соответственно.

Выходные данные

Выведите последовательность прыжков лягушек для достижения поставленной цели. Каждый прыжок можно задать одним числом — номером прыгающей лягушки (поскольку свободная кочка всегда ровно одна). Пронумеруем всех лягушек в соответствии с их начальным положением. Зеленые лягушки будут пронумерованы числами от 1 до N, а коричневые — с N+1 до N+M в порядке слева направо.

В первую строку выходного файла выведите число K — количество прыжков. K не должно превышать 107. Далее выведите K чисел — номера лягушек.

Если же достичь требуемой рассадки лягушек нельзя, выведите одно число –1.

Примеры
Входные данные
2 1
Выходные данные
5
2 3 2 1 3
#1707
Рисунки и пустоты
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Представьте себе бесконечную клетчатую бумагу. Изначально все клетки белые, но некоторые из них можно закрасить черным.

Назовем две клетки 8-связными, если у них есть общая сторона или точка. 8-путем назовем последовательность клеток от A до B, так что все клетки в последовательности черные, и две соседние клетки в последовательности являются 8-связными. Набор черных клеток назовем рисунком, если существует 8-путь из каждой клетки набора в любую другую клетку этого набора.

Назовем две клетки 4-связными, если у них есть общая сторона. 4-путем назовем последовательность клеток от A до B, так что все клетки в последовательности белые, и две соседние клетки в последовательности являются 4-связными. Конечный набор белых клеток назовем пустотой, если существует 4-путь из каждой клетки набора в любую другую клетку этого набора и к нему невозможно добавить ни одной белой клетки так, чтобы предыдущее условие не нарушилось.

Будем говорить, что рисунок имеет высоту H и ширину W если он охватывается прямоугольником с высотой H и шириной W и не охватывается никаким прямоугольником меньшего размера. На иллюстрации показан рисунок с высотой 7 и шириной 9. По заданным числа H, W и N постройте рисунок высоты H, ширины W содержащий ровно N пустот.

Входные данные

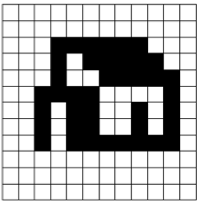
Входной файл содержит несколько тестовых блоков. Первая строка содержит число T (1 ≤ T ≤ 100) – количество тестовых блоков.

Каждая из следующих T строк описывает один тестовый блок. Описание состоит из целых чисел H, W и N (1 ≤ H, W ≤ 20, 1 ≤ N ≤ 200).

Выходные данные

Выходной файл должен содержать следующую информацию для каждого тестового блока:

Если рисунок можно построить, то выведите любую допустимую фигуру, удовлетворяющую условию задачи, состоящую из H строк по W символов в каждой. Выводите символ “.” для обозначения черной клетки и символ “#” для обозначения белой клетки.

Если рисунок построить нельзя, выведите одну строку, содержащую слово “Impossible”.

Вывод данных для разных тестовых блоков разделяйте одной пустой строкой.

Примеры тестов
Входные данные
3
7 9 2
20 20 22
5 5 10
Выходные данные
#......##
#.#.....#
#.##.....
....####.
.#..##.#.
.#..##.#.
.#.......

.#####.######.#####.
..###...####...###..
...#.....##.....#...
....................
....##..##..#...#...
...#.#.#..#.##.##...
...###.#....#.#.#...
...#.#.#..#.#...#...
...#.#..##..#...#...
....................
....................
.###..##..###...##..
..#..#..#.#..#.#..#.
..#..#....###..#....
..#..#..#.#....#..#.
.###..##..#.....##..
....................
...#.....##.....#...
..###...####...###..
.#####.######.#####.

Impossible
#2517
Следующее разбиение на слагаемые
  
Источники: [ Командные олимпиады, ВКОШП, 2009, Задача H ]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Разбиения числа \(n\) на слагаемые — это набор целых положительных чисел, сумма которых равна \(n\). При этом разбиения, отличающиеся лишь порядком слагаемых, считаются одинаковыми, поэтому можно считать, что слагаемые в разбиении упорядочены по неубыванию.

Например, существует 7 разбиений числа 5 на слагаемые:

5 = 1 + 1 + 1 + 1 + 1

5 = 1 + 1 + 1 + 2

5 = 1 + 1 + 3

5 = 1 + 2 + 2

5 = 1 + 4

5 = 2 + 3

5 = 5

В приведенном примере разбиения упорядочены лексикографически — сначала по первому слагаемому в разбиении, затем по второму, и так далее. В этой задаче вам потребуется по заданному разбиению на слагаемые найти следующее в лексикографическом порядке разбиение.

Входные данные

Входной файл содержит одну строку — разбиение числа \(n\) на слагаемые (\(1 \le n \le 100 000\)). Слагаемые в разбиении следуют в неубывающем порядке.

Выходные данные

Выведите в выходной файл одну строку — разбиение числа \(n\) на слагаемые, следующее в лексикографическом порядке после приведенного во входном файле. Если во входном файле приведено последнее разбиение числа \(n\) на слагаемые, выведите «No solution».

Примеры
Входные данные
5=1+1+3
Выходные данные
5=1+2+2
Входные данные
5=5
Выходные данные
No solution
Страница: << 1 2 3 4 5 6 7 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест