Теория вероятностей(3 задач)
Конструктив(21 задач)
Формула(17 задач)
Комбинаторика(9 задач)
Два студента, Адам и Антон, отмечают двухлетний юбилей несдачи их экзамена по математической логике. После тщательного поиска в местном супермаркете они купили прямоугольный торт и две свечи. Позже в университетском городке Адам поставил свечи в различные целочисленные точки пирога и дал нож Антону, чтобы он разрезал торт. Срез должен начинаться и заканчиваться в целочисленных точках на краях пирога, и не должен касаться свеч. Кроме того, каждая часть должна содержать ровно одну свечу. Пожалуйста, помогите Антону найти начальную и конечную точки разреза.
7 3 2 2 3 2
2 0 3 3
Боб нашёл отличную задачу для детей из его старой книги по математике. В ней сказано: Есть 10 детей, стоящих в кругу, 5 из них стоят рядом с мальчиком, и 7 из них стоят рядом с девочкой. Как такое могло быть? Вот решение этой задачи. Если 4 мальчика и 6 девочек стоят следующим образом: BGBGBGBGGG, Здесь 5 детей стоят рядом с мальчиком (здесь они выделены: BGBGBGBGGG), и 7 детей, которые стоят рядом с девочкой (BGBGBGBGGG). Теперь Боб хочет решить расширенную версию этой задачи: Есть n детей, стоящих в кругу, x из них стоят рядом с мальчиком, а y из них стоят рядом с девочкой. Как такое могло быть? Помогите Бобу написать эту программу в расширенной версии.
1
1
10 5 7
GBGGGBGBGB
10 3 8
Impossible
Назовём неподвижной точкой перестановки такой индекс i , что a i = i . Посчитайте число перестановок длины n , в которых нет неподвижных точек. Так как это число может быть воистину огромным, выведите его по модулю 10 9 + 7 .
В единственной строке входного файла задано целое число n ( 1 ≤ n ≤ 10 7 ) — количество элементов в перестановке.
В единственной строке выведите количество перестановок из n элементов без неподвижных точек, взятое по модулю 10 9 + 7 .
n ≤ 10 — 30 баллов.
n ≤ 5000 — 40 баллов.
n ≤ 10 6 — 20 баллов.
n ≤ 10 5 — 10 баллов.
3
2
Миша поспорил с друзьями, что решит N олимпиадных задач по программированию, потратив на это не более M дней. Следующие M дней Миша провел за решением задач и выиграл спор — всего он решил ровно N задач. В день i Миша решил X i задач. При этом Миша оценивал результаты своей работы за день следующим образом. Сначала он вычислял значение Y i — сколько в среднем нужно решать задач в оставшиеся дни (включая текущий), чтобы в итоге решить ровно N задач (с учетом уже решенных задач в предыдущие дни). Разумеется, число Y i не обязательно получалось целым. Если реальное количество задач X i , решенных Мишей в день i , совпадало со значением Y i , то Миша записывал на листочек символ «=». Если получалось так, что Миша решил меньше планируемого числа задач, то он записывал символ «<». Если же Миша решил больше задач, чем Y i , то записывал символ «>». Зная количество решенных в каждый из дней задач, необходимо восстановить записи Миши.
В первой строке содержатся 2 натуральных числа N и M — количество задач, которые должен решить Миша, и количество дней, отведенных для решения ( 1 ≤ N , M ≤ 100 ). Во второй строке записано M целых неотрицательных чисел X i —количество задач, решенных Мишей в соответствующий день. Гарантируется, что сумма всех чисел X i равна N .
Выведите одну строку из M символов — запись Миши (без пробелов).
В первом примере Миша должен решить 4 задачи за 2 дня, то есть в среднем по 2 задачи в день. Поскольку каждый день он так и решал по 2 задачи, то на листочке он записал два раза символ «=». Во втором примере нужно решить 12 задач за 4 дня. Соответственно, к первому дню Миша должен решать в среднем 3 задачи. Решив 3 задачи, он записал символ «=», у него осталось 9 задач и 3 дня. Во второй день Миша осилил только 2 задачи, что меньше среднего необходимого числа, поэтому на листочке он записал символ «<». У Миши осталось 7 задач и 2 дня, то есть в среднем он должен решать по 3.5 задачи в день. Миша решил 5 задач, что больше среднего, поэтому записал символ «>». Далее у Миши осталось 2 задачи и 1 день, то есть в среднем он должен решать по 2 задачи. В итоге, решив эти 2 задачи, Миша записал символ «=».
4 2 2 2
==
12 4 3 2 5 2
=<>=
Программистам Пете и Гене поручили разработать новый план королевства. Они долго рассуждали и сошлись на мнении, что в идеальном королевстве должно быть ровно N городов и ровно M дорог. Каждая из M дорог должна соединять два различных города, при этом между каждой парой городов может проходить не более одной дороги. Однако между какими именно городами будут проходить дороги, программисты не обсуждали. Они решили, что каждый из них нарисует свою карту дорог идеального королевства, а потом они выберут, чья карта лучше. Начинающий программист Миша, задумался, а стоит ли им вообще выбирать? Может быть, все возможные карты, содержащие N городов и M дорог одинаковые? Миша считает две карты дорог одинаковыми, если можно так пронумеровать города первой карты числами от 1 до N и города второй карты (тоже числами от 1 до N ), что дорога между некоторыми городами в первой карте существует тогда и только тогда, когда существует дорога между соответствующими городами второй карты. Например, карты, показанные на рисунке 1, являются одинаковыми, а на рисунке 2 — различными. По заданным числам N и M определите, могут ли существовать две различные карты дорог.
рисунок 1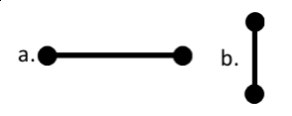 рисунок 2
рисунок 2
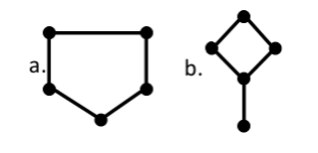
В первой строке содержатся два целых числа — N и M ( 1 ≤ N ≤ 10 , 0 ≤ M ≤ 45 ). Гарантируется, что существует хотя бы одна карта с N городами и M дорогами.
Если существуют две различные карты дорог, то выведите YES. В противном случае — NO.
Все карты из 2 городов и 1 дороги одинаковые (они соответствуют картам, изображенным на рисунке 1), поэтому не существует двух различных карт и ответ в первом примере NO. На рисунке 2 изображены две различные карты с 5 городами и 5 дорогами, поэтому во втором примере ответ YES.
2 1
NO
5 5
YES