#3360

Авиалинии

Темы: [Обход в глубину]

Компоненты сильной связности

В Берляндии скоро появятся свои авиалинии. Комитет по разработке берляндских авиалиний уже предложил свой вариант соединения городов авиарейсами. Каждый авиарейс задается парой различных городов. Рейсы односторонние. Президенту понравился план, однако он показался ему чересчур неэкономным. Требуется разработать новый план, который содержит наименьшее количество авиарейсов и удовлетворяет условию: если из города a можно было попасть в город b (возможно, с пересадками) согласно первоначальному плану, то и в новом плане это должно быть возможным. Если же это было сделать невозможно, то и согласно новому плану это не должно быть возможным. Очевидно, что из любого города можно попасть в него самого.

Входные данные

В первой строке входного файла записаны целые числа \(N\) и \(M\) (\(1 \leq N \leq 1000\), \(0 \leq M \leq 10000\)), где \(N\) – количество городов в стране, а \(M\) – количество авиарейсов в первоначальном плане. Города нумеруются от 1 до \(N\). Далее записано \(M\) пар различных чисел \(a_i\), \(b_i\) обозначающих наличие рейса из \(a_i\) в \(b_i\) в первоначальном плане (\(1 \leq a_i \leq N\), \(1 \leq b_i \leq N\)). Пары разделяются пробелами или переводами строк. Между парой городов может быть более одного авиарейса.

Выходные данные

В первую строку выходного файла выведите количество рейсов в новом плане. Далее выведите авиарейсы в формате, аналогичном формату входных данных. Пары разделяйте пробелами или переводами строк. Пары выводите в любом порядке. Если существует несколько решений, выведите любое.

Примечание

Тесты при \(N \le 20\), \(M \le 40\) оцениваются в 40 баллов и только при прохождении всех тестов группы.

Остальные тесты оцениваются независимо, но только при прохождении всех тестов первой группы.

Примеры

Входные данные

4 5
1 2 2 3 2 1 3 2 2 4

Выходные данные

4
1 3 3 2 2 1 2 4

#3361

Bugs

Темы: [Динамическое программирование по профилю]

Ограничение по времени – 10 секунд.
Ограничение по памяти – 64 мегабайта.
Компания Bugs начинает выпуск планки оперативной памяти Q-RAM размером 6 террабайт. Каждая планка состоит из 6 квадратных микросхем в форме прямоугольника \(3\times 2\). В результате технологического процесса, используемого в компании Bugs, получается прямоугольная область, разделенная на \(N\times M\) квадратных микросхем. После этого микросхемы тщательно проверяются и битые микросхемы помечаются черным маркером.

После этого, область разрезается на отдельные планки размером \(3\times 2\)(или \(2\times 3\)). Естественно, ни одна планка не должна содержать битых микросхем. Может возникнуть такая ситуация, что не все хорошие микросхемы войдут в какую-либо планку. Однако для снижения себестоимости компания хочет изготовить из произведенной области как можно больше планок.
На вход вашей программе будет даваться размер области и список битых микросхем на ней. Для этой области вам необходимо определить максимальное количество планок, которое можно вырезать из нее.

Входные данные

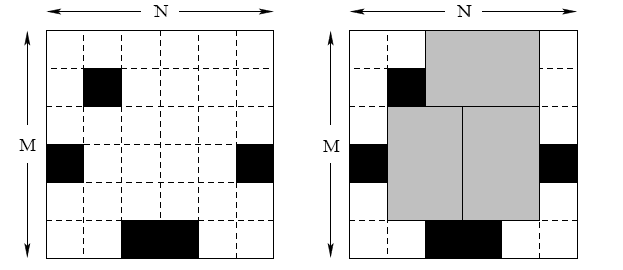
Первая строка содержит три целых числа \(N\), \(M\) и \(K\) (\(1\leq N\leq 150\), \(1 \leq M \leq 10\), \(0 \leq K \leq M\times N\)), где \(N\) – длина области, \(M\) – ее ширина, а \(K\) – количество битых микросхем. Следующие K строк содержат описание битых микросхем. Каждая из них содержит координаты битой микросхемы в виде двух целых чисел \(x\) и \(y\) (\(1 \leq x \leq N\), \(1 \leq y \leq M\)).

Выходные данные

Для каждой области выведите максимальное количество планок, которое может быть вырезано из нее на отдельной строке.

Примеры

Входные данные

Выходные данные

Входные данные

Выходные данные

#3362

Максимальный квадрат

Темы: [Дерево отрезков, RSQ, RMQ] ["Два указателя"]

На плоскости задан прямоугольник размером \(W\times H\), и \(N\) отмеченных точек внутри него. Требуется найти квадрат максимального размера:
со сторонами, параллельными сторонам прямоугольника;
не содержащий отмеченных точек строго внутри себя (но, возможно, содержащий отмеченные точки на границе);
лежащий внутри прямоугольника.

Входные данные

Первая строка входного файла содержит числа \(N\) — количество отмеченных точек, \(W\) — ширину прямоугольника и \(H\) — высоту прямоугольника (\(1 \leq N \leq 3 * 10^4\), \(0 \leq W, H \leq 10^6\)). Следующие \(N\) строк содержат координаты отмеченных точек \(X_i\), \(Y_i\) (целые числа, \(0 \leq X_i \leq W\), \(0 \leq Y_i \leq H\)). Система координат введена так, что вершины прямоугольника имеют координаты \((0, 0)\), \((W, 0)\), \((0, H)\), \((W, H)\).

Выходные данные

Выведите в выходной файл одно число — длину стороны максимального искомого квадрата.

Примеры

Входные данные

Выходные данные

Входные данные

1 10 10
5 5

Выходные данные

#3363

Палиндромность

Темы: [Динамическое программирование по подстрокам]

Напомним, что палиндромом называется строка, которая читается одинаково как слева направо, так и справа налево. Например, палиндромами являются строки «abba» и «madam».
Для произвольной строки s введем операцию деления пополам, обозначаемую half(s). Значение half(s) определяется следующими правилами:
Если s не является палиндромом, то значение half(s) не определено;
Если s имеет длину 1, то значение half(s) также не определено;
Если s является палиндромом четной длины 2m, то half(s) — это строка, состоящая из первых m символов строки s;
Если s является палиндромом нечетной длины 2m + 1, большей 1, то half(s) — это строка, состоящая из первых m + 1 символов строки s.
Например, значения half(inforamatics) и half(i) не определены, half(аbbа) = ab, half(madam) = mad. Палиндромностью строки s будем называть максимальное число раз, которое можно применить к строке s операцию деления пополам, чтобы результат был определен.
Например, палиндромность строк «informatics» и «i» равна 0, так как к ним нельзя применить операцию деления пополам даже один раз. Палиндромность строк «abba» и «madam» равна 1, а палиндромноств строки «totottotot» равна 3, посколвку операция деления пополам применима к ней три раза:
«totottotot» —> «totot» —> «tot» —> «to».
Задана некоторая строка s. Необходимо изменить в ней минимальное число символов так, чтобы ее палиндромность стала равной k.

Входные данные

Первая строка входного файла содержит число k (\(0 \leq k \leq 20\)). Вторая строка входного файла содержит непустую строку s, состоящую из строчных букв латинского алфавита. Ее длина не превосходит \(10^5\) символов.

Выходные данные

В выходной файл выведите минимальное число символов, которое требуется изменить, или —1, если требуемым образом изменить строку невозможно.

Примеры

Входные данные

2
abaabc

Выходные данные

Входные данные

1
ababa

Выходные данные

Входные данные

2
aa

Выходные данные

-1

#3364

Облака

Темы: [Элементарная геометрия]

Принадлежность отрезков многоугольникам

На небе находится \(N\) облаков, и все они двигаются, под воздействием ветра, с постоянной скоростью \(v = (v_x, v_y)\). Т.е. для любого вещественного числа \(t \leq 0\) любая точка любого облака с начальными координатами \((x, y)\) переместится в точку (\(x + t \times v_x\), \(y + t \times v_y\)). В нашей модели облака будут задаваться как многоугольники (включающие свою границу), вершины которых изначально имеют целые координаты. Многоугольники не имеют самопересечений и самокасаний. Облака могут пересекаться друг с другом. На земле находится центр управления спутником (расположенный в точке (0, 0)), а ровно над ним, выше облаков, находится спутник. Центр осуществляет постоянный обмен данными со спутником с помощью лазерного луча. Когда на пути лазерного сигнала находится облако, коммуникация невозможна. В начальный момент времени коммуникация со спутником возможна. За время наблюдения может возникнуть несколько моментов, в которые коммуникация со спутником невозможна, когда луч лазера прерывается одним или несколькими облаками. Ваша задача состоит в том, чтобы написать программу, определяющую количество интервалов времени, когда коммуникация была невозможна.

Входные данные

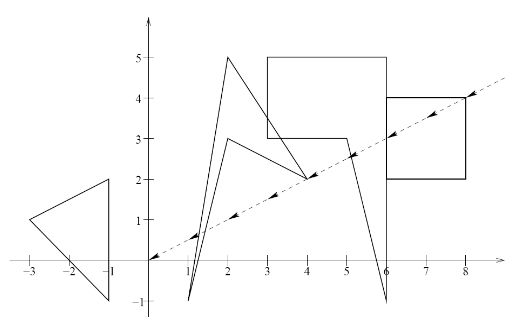
В первой строке задано три целых числа \(N\), \(v_x\), \(v_y\) (\(1 \leq N \leq 1000\), \(-10^9 \leq v_x, v_y \leq 10^9\)), где \(N\) – количество облаков, а \(v_x\) и \(v_y\) задают скорость ветра. X-координата задает направление с запада на восток, а Y-координата – направление с севера на юг. Следующие N строк содержат описание облаков. Каждое облако описывается с помощью числа K (\(1 \leq K \leq 1000\)) – количества вершин, задающих облако, а также \(2\times K\) целых чисел – координаты вершин облака в порядке \(x_1\), \(y_1\), \(x_2\), \(y_2\), ..., \(x_N\), \(y_N\). Координаты по модулю не превосходят \(10^9\).

Выходные данные

Выходной файл должна содержать единственное число – количество интервалов времени, в которые спутник был недоступен.

Примечание

В данном примере центр управления два раза накрывается облаком 2 и один раз облаками 1 и 4.

Примеры

Входные данные

4 -2 -1
4 6 2 6 4 8 4 8 2
4 2 3 1 -1 2 5 4 2
3 -3 1 -1 2 -1 -1
5 5 3 3 3 3 5 6 5 6 -1

Выходные данные