Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
Вчера у Васи был счастливый день: он наконец дописал программу всей своей жизни! И, недолго думая, он тут же запустил ее на Самом Главном Тесте.
Программа Васи очень сложная, и потому работает она долго. Поэтому Вася пошел спать, а наутро, сегодня, обнаружил, что программа, вместо того, чтобы посчитать нужный Ответ, вылетела с непонятной ошибкой.
Вася понял, что напрасно он не тестировал программу. Ведь Самый Главный Тест очень сложный — в нем есть \(N\) отдельных подзадач, и каждую из них надо решить. Конечно, надо было бы начать тестирование с меньшего количества подзадач, но ведь Вася — очень умный программист! И он абсолютно уверен, что его программа корректно решила все подзадачи, кроме какой-то одной. Вот только Вася не знает, какой именно.
Вася может изменять Самый Главный Тест, отключая в нем те или иные подзадачи. Он надеется, что, если среди отключенных будет та подзадача, на которой его программа не работает, то получившийся тест его программа спокойно пройдет. Но вот проблема: программа работает долго, а подзадач много, и потому, если отключать задачи по одной, то придется очень долго искать нужную. А Вася очень хочет узнать, где ошибка, уже завтра!
К счастью, у Васи в распоряжении есть много компьютеров. Он может на некоторых из них запустить свою программу на каком-то тесте (т.е. на Самом Главном Тесте с некоторыми отключенными подзадачами), а назавтра посмотреть, какие программы завершились успешно, а какие нет, — и по результатам понять, какая подзадача создавала проблемы. Помогите Васе подобрать тесты для каждого из компьютеров, т.е. объясните ему, какие подзадачи в каком тесте он должен отключить, так, чтобы назавтра, узнав результаты работы программы на этих тестах, он смог бы уверенно определить, с какой подзадачей у него возникают проблемы (естественно, считая, что такая подзадача только одна, ведь Вася — очень умный программист!)
Учтите, что Васе не хочется делать лишнюю работу по запуску программ и определению их результата, поэтому он хочет минимизировать количество запусков (т.е. фактически количество компьютеров, ведь его программа настолько сложная, что на одном компьютере можно запустить только один экземпляр программы).
В первой и единственной строке входного файла находится одно целое число \(N\) — количество подзадач в Самом Главном Тесте (\(1 \le N \le 10^5\)).
В первой строке выходного файла выведите минимальное необходимое количество компьютеров \(M\). В последующих \(M\) строках выведите информацию о том, на каком тесте надо запускать программу на каком компьютере. А именно, в \(i\)-ую из них выведите последовательность чисел \(k_i\), \(b_{i1}\), \(b_{i2}\), ...., \(b_{ik_i}\), где \(k_i\) — количество подзадач, которые надо отключить в тесте, на котором будет работать программа на \(i\)-ом компьютере, а \(b_{ij}\) (\(1 \le j \le k_i\), \(1 \le b_{ij} \le N\)) — номера подзадач, которые надо отключать. Числа \(b_{ij}\) должны быть различны для каждого фиксированного \(i\).
Подзадачи нумеруются от 1 до \(N\).
В пределах одной строки подзадачи можете выводить в любом порядке. Если есть несколько оптимальных решений, выведите любое.
В примере:
5
3 3 1 3 5 3 1 2 5 4 1 2 3 4
В игре «Руммикуб» используются фишки, которые бывают четырех различных цветов, и на каждой из которых написано одно натуральное число от 1 до 13. Для каждого числа и для каждого цвета в наборе фишек есть ровно две соответствующие фишки, т.е. всего в наборе \(8\cdot 13 = 104\) фишки.
Число, написанное на фишке, будем называть ее достоинством; цвета будем обозначать латинскими буквами A, B, C и D, и каждую фишку будем обозначать, записывая сначала ее цвет, а потом — ее достоинство. Например, C12 — это фишка цвета C и достоинством 12.
Комбинацией в игре называется набор из как минимум трех фишек, удовлетворяющий любому из следующих условий:
Например, следующие наборы фишек являются комбинациями:
C12, A12, B12;
C12, A12, B12, D12;
C5, C6, C7;
A3, A4, A5, A6, A7.
При этом следующие наборы не являются комбинациями:
A3, B3 (слишком мало фишек);
A3, B3, C3, D3, B3 (цвета повторяются);
A3, A4, A4, A5, A6 (достоинства повторяются);
A3, A4, A6, A7, A8 (число 5 пропущено).
Одна из основных задач в руммикубе состоит в том, чтобы данный набор фишек распределить на комбинации так, чтобы каждая фишка входила ровно в одну комбинацию. Напишите программу, которая будет это делать.
В первой строке входного файла находится одно натуральное число \(K\) — количество фишек. Далее следуют \(K\) строк, на каждой из которых находится описание одной фишки — цвет и достоинство.
Гарантируется, что эти фишки являются корректным подмножеством фишек из некоторого комплекта для игры в руммикуб; т.е. гарантируется, что каждый цвет — это латинская заглавная буква от A до D, что каждое достоинство — это натуральное число, не превосходящее 13, и что для для каждой пары (цвет, достоинство) в наборе есть не более двух таких фишек.
Если данный набор фишек можно разбить на комбинации так, чтобы каждая фишка входила ровно в одну комбинацию, то в первую строку выходного файла выведите одно число \(M\) — количество комбинаций в вашем решении. Далее выведите \(M\) строк, в \(i\)-ой из которых выведите \(i\)-ую комбинацию. А именно, сначала выведите количество фишек в комбинации, а потом сами фишки, разделенные между собой и отделенные от количества фишек пробелами. В пределах каждой комбинации фишки можете выводить в произвольном порядке; комбинации также можете выводить в произвольном порядке.
Если есть несколько решений, выведите любое. Если решений нет, то выведите в выходной файл одно число -1.
3 A2 A3 A5
-1
3 A2 A4 A3
1 3 A2 A4 A3
7 A12 A13 A13 B13 C13 D13 A11
2 3 A11 A12 A13 4 A13 B13 C13 D13
Во время летних каникул Вася и Петя путешествовали со своими родителями по Одной Очень Гостеприимной Стране. В этой стране всего N городов, пронумерованных числами от 1 до N. Маршрут Васи начинался в городе A и заканчивался в городе B, а маршрут Пети – начинался в городе C и заканчивался в городе D. Поскольку времени у них было немного, то и Васины и Петины родители выбрали самый короткий путь, соединяющий начальный и конечный города их маршрута.
После каникул Вася с Петей встретились и захотели обсудить свои путешествия. Особенно интересно было обсуждать те города, в которых побывали они оба.
Определите, в каких городах побывали и Вася и Петя и выведите их номера в порядке возрастания. Если же маршруты ребят не пересекались, выведите -1.
Обратите внимание на то, что поскольку на некоторых дорогах шел ремонт, то длина пути от города X в город Y может отличаться от длины пути от города Y в город X.
В первой строке вводится число N (1 ≤ N ≤ 100). В следующих N строках вводится по N чисел, не превосходящих 100, j-ое число в i-ой строке равно длине пути между i-м и j-м городом. Известно, что между любыми двумя городами есть дорога и поскольку на некоторых дорогах идет ремонт, то длина пути от города X в город Y может отличаться от длины пути от города Y в город X. В следующих двух строках вводятся пары целых числа от 1 до 100 – номера городов, являющихся началом и концом маршрута Васи (A и B), и аналогичные числа для Пети (C и D).
Выведите их номера в порядке возрастания. Если маршруты ребят не пересекались, выведите одно число - 1. Гарантируется, что кратчайший путь – единственный.
4
0 100 100 1
100 0 3 100
100 4 0 1
100 3 10 0
1 3
2 3
2 3
В сказочной стране, столицей которой является Изумрудный Город, всего N городов. Некоторые города соединены дорогой, целиком вымощеной желтым кирпичем. Элли нужно добраться из города на границе в Изумрудный Город и затем вернуться обратно. Чтобы не было скучно, ей хочется добираться туда и обратно разным маршрутом (а именно так, чтобы ни одна из дорог не была и на маршруте туда и на маршруте обратно). Поскольку зря тратить время она не собирается, то для каждого пути она хочет выбрать самый короткий вариант.
Напишите программу, которая поможет Элли определить, возможно ли такое путешествие, и если оно возможно, то разработает для нее маршрут.
Все города пронумерованы натуральными числами от 1 до N, город на границе имеет номер K, Изумрудный Город имеет номер N.
В первой строке содержатся три числа: N, K и M (1 ≤ N ≤ 100, 1 ≤ K < N, 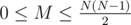 ), где N -– количество городов в Сказочной стране, K – номер города, из которого Элли начинает путешествие, M – количество дорог, мощеных желтым кирпичем. В следующих M строках вводятся по три числа – номера городов, соединенных дорогой из желтого кирпича и длина этой дороги.
), где N -– количество городов в Сказочной стране, K – номер города, из которого Элли начинает путешествие, M – количество дорог, мощеных желтым кирпичем. В следующих M строках вводятся по три числа – номера городов, соединенных дорогой из желтого кирпича и длина этой дороги.
В первой строке выведите -1, если желание Элли неосуществимо. В противном случае в первой строке выведите два числа: длину пути туда и длину пути обратно, а в следующих двух строках: номера городов на пути туда и на пути обратно в том порядке, в котором она будет их проходить.
4 1 6
1 4 3
2 4 2
2 3 1
1 2 5
1 3 6
4 3 8
3 7
1 4
4 2 1
4 1 0
-1
В целях увеличения продаж фирма "Новый русский шоколад" приняла решение разбивать каждую плитку на дольки в форме прямоугольников 1 × 2 и уголков (квадрат 2 × 2 с вырезанной угловой клеткой), а не на скучные квадратики 1 × 1. При этом долек другой формы на плитке шоколада быть не должно. Через некоторое время узор на плитке будет меняться на другой (но по-прежнему состоящий только из прямоугольников 1 × 2 и уголков), через некоторое время – еще на другой и так далее. Директору фирмы "Новый русский шоколад" захотелось узнать, а сколько всего существует способов разбить плитку шоколада на такие дольки? Помогите ему найти ответ.
В одной строке вводятся два натуральных числа n и m – ширина и длина плитки (1 ≤ n, m ≤ 9).
Выведите одно целое число – количество способов разбить плитку шоколада размером n × m на прямоугольники 1 × 2 и уголки (и прямоугольник и уголок можно поворачивать, долек другой формы на плитке быть не должно).
2 3
5
3 3
8