Обход в глубину(100 задач)
Способы задания графа(54 задач)
Минимальный каркас(12 задач)
Потоки(21 задач)
Паросочетания(17 задач)
Эйлеров цикл(9 задач)
Деревья(16 задач)
Сеть компьютерных салонов «ХТТП» представлена в городе Н. двумя магазинами. Руководство Н-ского отделения сети решило реорганизовать витрины, на которых представлены ноутбуки. В каждом из двух магазинов на витрине должны быть представлены \(N\) моделей ноутбуков, выставленные в ряд от касс вглубь помещения магазина. Маркетологи каждого из магазинов уже определили порядок, в котором на витрине должны быть расположены эти модели (эти порядки в двух магазинах, конечно же, могут быть разными).
На витрины надо выставлять специальные, выставочные, образцы ноутбуков, с соответствующим программным обеспечением, показывающим рекламу, и т.д. В распоряжении администрации компьютерных салонов есть две версии специализированного ПО: работающие под управлением операционных систем Windows и Linux. Соответственно, каждый из выставочных образцов ноутбуков должен иметь предустановленной ровно одну из этих систем.
Для снижения затрат было принято решение закупить по два идентичных экземпляра каждой модели ноутбуков (т.е. с одинаковыми предустановленными операционными системами), отправить по одному экземпляру в каждый из магазинов сети, и расставить их на витрине в соответствии с порядком, определенным маркетологами того магазина.
Но при этом возникла проблема. По требованиям Федеральной антимонопольной службы, компьютерные салоны не должны предоставлять преимущества ни одной из операционных систем. Начальство сети «ХТТП» знает, как проходит проверка на соответствие этой норме законодательства. Инспектор антимонопольной службы идет по магазину начиная от касс вдоль витрины с ноутбуками, считает отдельно количество встреченных ноутбуков с Windows и Linux, а также модуль разности этих чисел (т.е. на сколько ноутбуков с одной системой он встретил больше, чем ноутбуков с другой системой). В некоторый момент он останавливается и говорит: «Ага!». Это значит: слишком у вас большой дисбаланс между операционными системами, поэтому платите штраф. Размер штрафа пропорционален разнице (взятой по модулю) количества ноутбуков с разными системами, которые увидел инспектор.
Естественно, руководство сети не в состоянии предсказать, в какой из магазинов пойдет инспектор, а также сколько ноутбуков он просмотрит. Тем не менее, они хотят минимизировать штраф, который им будет выписан в худшем случае. Помогите им.
Например, пусть \(N=5\): в магазинах должны быть выставлены пять моделей ноутбуков. Будем нумеровать модели ноутбуков от 1 до 5. Пусть в первом магазине маркетологи определили, что оптимальный порядок ноутбуков следующий (от касс вглубь зала):
2 4 1 3 5,
а во втором магазине —
3 1 2 5 4.
Тогда, если закупить ноутбуки моделей 1, 3 и 4 с операционной системой Windows, а 2 и 5 — с Linux, то порядок операционных систем в магазинах будет следующий (от касс вглубь зала):
L W W W L,
W W L L W.
Тогда, если, например, инспектор придет в первый магазин и просмотрит первые четыре ноутбука, то он скажет: «Ага!», и выпишет штраф за то, что он увидел Windows-ноутбуков на два больше, чем Linux. Аналогичный результат будет, если он придет во второй магазин и просмотрит только первые два ноутбука.
А если закупить ноутбуки 2 и 3 с системой Linux, а 1, 4, 5 — с Windows, то порядок операционных систем будет следующий:
L W W L W,
L W L W W,
и в какой бы магазин не пришел инспектор, и сколько бы ноутбуков он не посмотрел, разница Windows- и Linux-ноутбуков не будет превосходить по модулю 1, и это и будет оптимальным вариантом для руководства сети. (Напомним, что инспектор всегда начинает осмотр магазина от касс и идет вглубь магазина вдоль ряда с ноутбуками).
В первой строке входного файла записано одно число \(N\) (\(1\leq N\leq 10^5\)) — количество моделей ноутбуков, которые должны быть представлены на витрине. Модели ноутбуков нумеруются от 1 до \(N\).
Далее следуют две строки по \(N\) чисел в каждой — порядки моделей ноутбуков на витрине, определенные маркетологами первого и второго магазина, от касс вглубь зала. Гарантируется, что порядки корректные, т.е. что в каждой из этих строк все числа находятся в интервале от 1 до \(N\) и никакое из чисел не встречается в одной строке дважды.
В выходной файл выведите строку из \(N\) символов, описывающих необходимую конфигурацию ноутбуков. А именно, \(i\)-ый символ должен быть “W” (без кавычек), если \(i\)-ую модель ноутбуков надо закупать с предустановленной системой Windows, и “L” для Linux.
Если есть несколько оптимальных решений, выведите любое.
5 2 4 1 3 5 3 1 2 5 4
WLLWW
5 1 4 2 3 5 5 1 3 4 2
WLWLL
Во время летних каникул Вася и Петя путешествовали со своими родителями по Одной Очень Гостеприимной Стране. В этой стране всего N городов, пронумерованных числами от 1 до N. Маршрут Васи начинался в городе A и заканчивался в городе B, а маршрут Пети – начинался в городе C и заканчивался в городе D. Поскольку времени у них было немного, то и Васины и Петины родители выбрали самый короткий путь, соединяющий начальный и конечный города их маршрута.
После каникул Вася с Петей встретились и захотели обсудить свои путешествия. Особенно интересно было обсуждать те города, в которых побывали они оба.
Определите, в каких городах побывали и Вася и Петя и выведите их номера в порядке возрастания. Если же маршруты ребят не пересекались, выведите -1.
Обратите внимание на то, что поскольку на некоторых дорогах шел ремонт, то длина пути от города X в город Y может отличаться от длины пути от города Y в город X.
В первой строке вводится число N (1 ≤ N ≤ 100). В следующих N строках вводится по N чисел, не превосходящих 100, j-ое число в i-ой строке равно длине пути между i-м и j-м городом. Известно, что между любыми двумя городами есть дорога и поскольку на некоторых дорогах идет ремонт, то длина пути от города X в город Y может отличаться от длины пути от города Y в город X. В следующих двух строках вводятся пары целых числа от 1 до 100 – номера городов, являющихся началом и концом маршрута Васи (A и B), и аналогичные числа для Пети (C и D).
Выведите их номера в порядке возрастания. Если маршруты ребят не пересекались, выведите одно число - 1. Гарантируется, что кратчайший путь – единственный.
4
0 100 100 1
100 0 3 100
100 4 0 1
100 3 10 0
1 3
2 3
2 3
В сказочной стране, столицей которой является Изумрудный Город, всего N городов. Некоторые города соединены дорогой, целиком вымощеной желтым кирпичем. Элли нужно добраться из города на границе в Изумрудный Город и затем вернуться обратно. Чтобы не было скучно, ей хочется добираться туда и обратно разным маршрутом (а именно так, чтобы ни одна из дорог не была и на маршруте туда и на маршруте обратно). Поскольку зря тратить время она не собирается, то для каждого пути она хочет выбрать самый короткий вариант.
Напишите программу, которая поможет Элли определить, возможно ли такое путешествие, и если оно возможно, то разработает для нее маршрут.
Все города пронумерованы натуральными числами от 1 до N, город на границе имеет номер K, Изумрудный Город имеет номер N.
В первой строке содержатся три числа: N, K и M (1 ≤ N ≤ 100, 1 ≤ K < N, 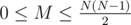 ), где N -– количество городов в Сказочной стране, K – номер города, из которого Элли начинает путешествие, M – количество дорог, мощеных желтым кирпичем. В следующих M строках вводятся по три числа – номера городов, соединенных дорогой из желтого кирпича и длина этой дороги.
), где N -– количество городов в Сказочной стране, K – номер города, из которого Элли начинает путешествие, M – количество дорог, мощеных желтым кирпичем. В следующих M строках вводятся по три числа – номера городов, соединенных дорогой из желтого кирпича и длина этой дороги.
В первой строке выведите -1, если желание Элли неосуществимо. В противном случае в первой строке выведите два числа: длину пути туда и длину пути обратно, а в следующих двух строках: номера городов на пути туда и на пути обратно в том порядке, в котором она будет их проходить.
4 1 6
1 4 3
2 4 2
2 3 1
1 2 5
1 3 6
4 3 8
3 7
1 4
4 2 1
4 1 0
-1
Дан неориентированный невзвешенный граф. Необходимо посчитать количество его компонент связности и вывести их.
Во входном файле записано два числа \(N\) и \(M\) (0 < \(N\) ≤ 100000, 0 ≤ \(M\) ≤ 100000). В следующих \(M\) строках записаны по два числа \(i\) и \(j\) (1 ≤ \(i\), \(j\) ≤ \(N\)), которые означают, что вершины \(i\) и \(j\) соединены ребром.
В первой строчке выходного файла выведите количество компонент связности. Далее выведите сами компоненты связности в следующем формате: в первой строке количество вершин в компоненте, во второй - сами вершины в произвольном порядке.
6 4 3 1 1 2 5 4 2 3
3 3 1 2 3 2 4 5 1 6
Дан неориентированный невзвешенный граф. Необходимо определить, является ли он деревом.
В первой строке входного файла содержится одно натуральное число \(N\) (\(N\) ≤ 100) - количество вершин в графе. Далее в \(N\) строках по \(N\) чисел - матрица смежности графа: в \(i\)-ой строке на \(j\)-ом месте стоит 1, если вершины \(i\) и \(j\) соединены ребром, и 0, если ребра между ними нет. На главной диагонали матрицы стоят нули. Матрица симметрична относительно главной диагонали.
Вывести "YES", если граф является деревом, и "NO" иначе.
6 0 1 1 0 0 0 1 0 1 0 0 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0
NO
3 0 1 0 1 0 1 0 1 0
YES