Бинарный поиск(101 задач)
Порядковые статистики(3 задач)
Поиск подстроки в строке(1 задач)
Тернарный поиск(8 задач)
"Два указателя"(18 задач)
Когда Петя учился в школе, он часто участвовал в олимпиадах по информатике, математике и физике. Так как он был достаточно способным мальчиком и усердно учился, то на многих из этих олимпиад он получал дипломы. К окончанию школы у него накопилось \(n\) дипломов, причём, как оказалось, все они имели одинаковые размеры: \(w\) — в ширину и \(h\) — в высоту. Сейчас Петя учится в одном из лучших российских университетов и живёт в общежитии со своими одногруппниками. Он решил украсить свою комнату, повесив на одну из стен свои дипломы за школьные олимпиады. Так как к бетонной стене прикрепить дипломы достаточно трудно, то он решил купить специальную доску из пробкового дерева, чтобы прикрепить её к стене, а к ней — дипломы. Для того чтобы эта конструкция выглядела более красиво, Петя хочет, чтобы доска была квадратной и занимала как можно меньше места на стене. Каждый диплом должен быть размещён строго в прямоугольнике размером \(w\) на \(h\). Дипломы запрещается поворачивать на 90 градусов. Прямоугольники, соответствующие различным дипломам, не должны иметь общих внутренних точек. Требуется написать программу, которая вычислит минимальный размер стороны доски, которая потребуется Пете для размещения всех своих дипломов.
Входной файл содержит три целых числа: \(w\), \(h\), \(n\) (\(1\le w,h,n\le 10^9\)).
В выходной файл необходимо вывести ответ на поставленную задачу.
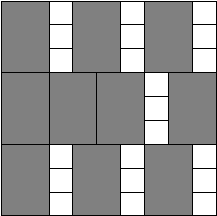
2 3 10
9
1 1 1
1
С детства Максим был неплохим музыкантом и мастером на все руки. Недавно он самостоятельно сделал несложный перкуссионный музыкальный инструмент — треугольник. Ему нужно узнать, какова частота звука, издаваемого его инструментом.
У Максима есть профессиональный музыкальный тюнер, с помощью которого можно проигрывать ноту с заданной частотой. Максим действует следующим образом: он включает на тюнере ноты с разными частотами и для каждой ноты на слух определяет, ближе или дальше она к издаваемому треугольником звуку, чем предыдущая нота. Поскольку слух у Максима абсолютный, он определяет это всегда абсолютно верно.
Вам Максим показал запись, в которой приведена последовательность частот, выставляемых им на тюнере, и про каждую ноту, начиная со второй, записано — ближе или дальше она к звуку треугольника, чем предыдущая нота. Заранее известно, что частота звучания треугольника Максима составляет не менее 30 герц и не более 4000 герц.
Требуется написать программу, которая определяет, в каком интервале может находиться частота звучания треугольника.
Первая строка входного файла содержит целое число \(n\) — количество нот, которые воспроизводил Максим с помощью тюнера (\(2\le n\le1000\)). Последующие \(n\) строк содержат записи Максима, причём каждая строка содержит две компоненты: вещественное число \(f_i\) — частоту, выставленную на тюнере, в герцах (\(30\le f_i\le4000\)), и слово «closer» или слово «further» для каждой частоты, кроме первой.
Слово «closer» означает, что частота данной ноты ближе к частоте звучания треугольника, чем частота предыдущей ноты, что формально описывается соотношением: \(|f_i-f_{треуг.}|<|f_{i-1}-f_{треуг.}|\).
Слово «further» означает, что частота данной ноты дальше, чем предыдущая.
Если оказалось, что очередная нота так же близка к звуку треугольника, как и предыдущая нота, то Максим мог записать любое из двух указанных выше слов.
Гарантируется, что результаты, полученные Максимом, непротиворечивы.
В выходной файл необходимо вывести через пробел два вещественных числа — наименьшее и наибольшее возможное значение частоты звучания треугольника, изготовленного Максимом. Числа должны быть выведены с точностью не хуже \(10^{-6}\).
3 440 220 closer 300 further
30.0 260.0
4 554 880 further 440 closer 622 closer
531.0 660.0
К очередной Летней компьютерной школе было решено подготовить кружки как для школьников, так и для всех преподавателей.
Имея привычку делать важные дела в самый последний момент, дизайнер закончил работу над макетом за два дня до начала школы. Ещё день уйдёт у завода-изготовителя на то, чтобы изготовить кружки и нанести на них изображение. На то, чтобы довезти кружки от завода-изготовителя до ЛКШ, остаётся всего 24 часа.
Заказ на 10000000 экземпляров кружек (а именно столько заказали организаторы), конечно же, за один рейс не увезти. Однако, за первый рейс хочется привезти максимальное количество кружек. Для перевозки был заказан один большегрузный автомобиль. Но есть один нюанс: на некоторых дорогах установлено ограничение на вес автомобиля. Поэтому если автомобиль нагрузить кружками под завязку, то, возможно, не удастся воспользоваться самым коротким маршрутом, а придётся ехать в объезд. Может случиться даже так, что из-за этого грузовик не успеет доехать до лагеря вовремя, а этого допустить никак нельзя. Итак, сколько же кружек можно погрузить в автомобиль, чтобы успеть привезти этот ценный груз вовремя, и не нарушая правил дорожного движения?
В первой строке находятся числа n (1≤n≤500) и m - количество узловых пунктов дорожной схемы и количество дорог, соответственно. В следующих m строках находится информация о дорогах. Каждая дорога описывается в отдельной строке следующим образом. Сначала указаны номера узловых пунктов, которые соединяются данной дорогой, потом время, которое тратится на проезд по этой дороге, и, наконец, максимальный вес автомобиля, которому разрешено ехать по этой дороге. Известно, что все дороги соединяют различные пункты, причем для каждой пары пунктов есть не более одной дороги, непосредственно их соединяющей. Все числа разделены одним или несколькими пробелами.
Узловые пункты нумеруются числами от 1 до n. При этом завод по производству кружек имеет номер 1, а ЛКШ - номер n. Время проезда по дороге задано в минутах и не превосходит 1440 (24 часа). Ограничение на массу задано в граммах и не превосходит одного миллиарда. Кроме того, известно, что одна кружка весит 100 грамм, а пустой грузовик - 3 тонны.
Выведите одно число - максимальное количество кружек, которое можно привезти за первый рейс, потратив не более 24часов.
3 3 1 2 10 3000220 2 3 20 3000201 1 3 1 3000099
2
В одной театральной кассе есть в продаже билеты любой стоимости, выражающейся натуральным числом. При покупке билетов по цене за билет от A до B рублей включительно нужно дополнительно оплатить сервисный сбор в размере C процентов от номинальной стоимости билетов (сервисный сбор не обязательно выражается целым числом рублей, но всегда выражается целым числом копеек). При покупке билетов стоимостью менее A рублей за билет, а также более B рублей за билет, сервисный сбор не берется.
У вас есть X рублей и вам нужно K билетов одинаковой цены (цена обязательно должна выражаться натуральным числом рублей, 0 не считается натуральным). Билеты какого самого дорогого номинала вы можете себе позволить?
Вводятся целые A, B, C, X, K (1 ≤ A ≤ B ≤ 109, 0 ≤ C ≤ 1000, 0 ≤ X ≤ 109, 1 ≤ K ≤ 100000).
Если на имеющиеся деньги невозможно приобрести ни одного билета, выведите 0. Иначе выведите натуральное число – номинальную стоимость приобретённых билетов.
Подзадача 1. Все числа \(\le100\) - 50 баллов.
Подзадача 2. Без дополнительных ограничений - 50 баллов.
1 10 0 5 5
1
10 100 50 50 5
9
10 100 50 100 5
13
В 2050 году руководство Глобальной Телефонной Сети (ГТС) приняло решение о новой системе тарификации коротких текстовых сообщений. Теперь цена отправки одного сообщения зависит от количества совпадающих цифр в начале номеров телефонов отправителя и получателя. Если первые \(c\) цифр телефонов совпадают, а \((c+1)\)-я цифра различается, то стоимость сообщения составляет \((10-c)\) кредитов (\(0\le c\le9\)). Все номера телефонов — десятизначные. При этом ГТС разрешает каждому абоненту отправлять сообщение только в пределах часового пояса своего проживания или часовых поясов, отличающихся от него на 1 час.
Школьник Поликарп из Ханты-Мансийска (время +2 часа от московского) успешно решил все задания первого тура олимпиады школьников по информатике. Теперь он желает сообщить об этом в Париж (время −2 часа от московского) своему учителю — профессору де Коде́ру. Так как Ханты-Мансийск и Париж находятся не в соседних часовых поясах, Поликарп не может послать сообщение напрямую. Поэтому он пользуется тем, что у него есть друзья, которые проживают в Ханты-Мансийске, Париже, а также в промежуточных часовых поясах — в Дубае (время +1 час от московского), Москве и Калининграде (время −1 час от московского). Друзья Поликарпа по цепочке доставят профессору де Коде́ру столь важную информацию. Поликарп хочет организовать передачу информации таким образом, чтобы минимизировать суммарные расходы по отправке всех сообщений.
Напишите программу, определяющую цепочку доставки, для которой суммарная стоимость отправленных сообщений минимальна.
Первые две строки входного файла содержат телефонные номера Поликарпа и профессора де Коде́ра. Далее следуют 5 блоков данных, описывающих друзей Поликарпа, живущих в Ханты-Мансийске, Дубае, Москве, Калининграде и Париже, соответственно. Каждый блок начинается со строки, содержащей одно число \(n_i\) (\(1\le n_i\le100\,000\)) — количество друзей Поликарпа в соответствующем городе, после которой следуют \(n_i\) строк — номера телефонов друзей. Все номера телефонов состоят ровно из 10 цифр. Гарантируется, что сумма всех \(n_i\) не превосходит 100 000. Все номера телефонов во входных данных различны.
В первой строке выходного файла выведите минимальную возможную стоимость передачи информации \(w\) и количество задействованных в цепочке телефонных номеров \(k\). Далее выведите \(k\) номеров телефонов, описывающих саму цепочку, в порядке следования от Поликарпа к профессору де Коде́ру. Первый номер в цепочке должен совпадать с номером телефона Поликарпа, а последний — с номером телефона профессора де Коде́ра. Если решений несколько, выведите любое.
Система оценивания
2099013166 7043239909 1 0258442145 1 0000000000 1 0000000001 1 0000000002 1 0147571204
22 5 2099013166 0000000000 0000000001 0000000002 7043239909
4261802325 7967612531 1 8176476745 1 3084033164 1 1737248630 1 9447552231 1 2848478213
40 5 4261802325 3084033164 1737248630 9447552231 7967612531