Наиболее известная игра, дошедшая до нас из Японии – это Судоку. Новая игра должна затмить ее славу. Про нее известно следующее. Нам дан квадрат, разделенный сеткой на n×n клеток, а каждая клетка содержит картинку одного из k типов. Игрок должен переместить их, чтобы получить максимально возможное число одинаковых первых рядов (два ряда считаются одинаковыми, если оба заполнены одинаковыми картинками и в одинаковом порядке). По виду таблицы определите, сколько одинаковых рядов в ней можно сложить (если менять картинки как угодно).
Например, если нам дана такая таблица:
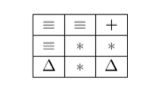
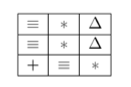
одно из результирующих состояний в игре будет
Первая строка входных данных содержит два числа n (\(1\leq n \leq 40000\)) и k (\(1 \leq k \leq 50000\)). Каждая из следующих k строк содержит число картинок в таблице каждого из k типов. Все числа больше 0, их сумма в точности равна \(n^2\).
Выведите в первой строке максимальное количество одинаковых рядов, которые можно построить из этих картинок. В следующих n строках выведите содержание таких рядов: в каждой строке должно находиться одно число – номер соответствующей картинке в порядке ее появления во входных данных. Если решений несколько, выведите любое из них.
3 4 3 3 2 1
2 1 2 3
Роман коллекционирует числа, кажущиеся ему интересными. Например, сейчас он считает интересным положительные числа, запись которых в системе счисления с основанием k заканчивается нечетным числом нулей. Например, при k = 2 такими числами являются 210 = 102, 2410 = 110002.
Для того, чтобы пополнить свою коллекцию, Роман хочет найти n-ое в порядке возрастания такое число. Поскольку n он взял достаточно большим, то вручную у него это сделать не получается. Помогите Роману — напишите программу, которая найдет число, которое нужно ему для пополнения коллекции.
Первая строка входного файла содержит два целых числа (1 ≤ n ≤ 1015, 2 ≤ k ≤ 10).
В выходной файл выведите n-ое в порядке возрастания число, запись которого в системе счисления с основанием k заканчивается на нечетное число нулей. Это число необходимо вывести в десятичной системе счисления.
1 2
2
10 10
110
Дима недавно поступил на работу в НИИ Плоских Кривых. Как следует из названия этого научно- исследовательского института, он занимается различными исследованиями в области плоских кривых. Недавно Димин начальник Георгий столкнулся с весьма интересной кривой, которая, как выяснилось после некоторого исследования, известна под названием Архимедовой спирали. Архимедова спираль плоская кривая, изображающая траекторию точки M, которая равномерно движется вдоль луча OK с началом в O, в то время как сам луч OK равномерно вращается вокруг точки O (см. рисунок). Другими словами, расстояние до начала координат ρ = OM линейно зависит от угла поворота φ луча OK. При этом повороту луча OK на один и тот же угол соответствует одно и то же приращение расстояния ρ.
Движение точки M можно задать с помощью ряда параметров:
• начального угла поворота α луча OK (измеряется в градусах против часовой стрелки относительно положительного направления оси OX);
• угловой скорости вращения ω луча OK (измеряется в градусах за единицу времени);
• начального расстояния R от точки M до начала координат (точки O);
• скорости движения V точки M по лучу OK.
Если, задав эти параметры, не ограничить время движения точки M, то получится бесконечная кривая, исследовать которую достаточно трудно. Поэтому Дима решил ограничиться исследованием некоторой части этой кривой той, которая получается при движении точки M от нулевого момента времени до момента времени T. Задача, которую решает Дима состоит в поиске прямоугольника минимальной площади со сторонами, параллельными осям координат, в который ее можно вписать.
Требуется написать программу, которая найдет искомый прямоугольник
Входной файл содержит четыре целых числа: ω (1 ≤ ω ≤ 100), V (1 ≤ V ≤ 100), R (0 ≤ R ≤ 100) и T (1 ≤ T ≤ 1000). В этой задаче считается, что начальный угол поворота α равен нулю.
В первой строке выходного файла выведите два вещественных числа — координаты левого нижнего угла искомого прямоугольника, а во второй строке — координаты правого верхнего угла искомого прямоугольника.
Ответ будет считаться правильным, если значение каждой из координат будет отличаться от истинного значения не более чем на 10-5.
60 10 0 18
-150.3028434716 -165.2754877824 180.0000000000 135.3362037333
На клетчатой плоскости закрашено K клеток. Требуется найти минимальный по площади прямоугольник, со сторонами, параллельными линиям сетки, покрывающий все закрашенные клетки.
Во входном файле, на первой строке, находится число K(1 ≤ K ≤ 100). На следующих K строках находятся пары чисел Xi и Yi – координаты закрашенных клеток (|Xi|, |Yi| ≤ 109).
Выведите в выходной файл координаты левого нижнего и правого верхнего углов прямоугольника.
3 1 1 1 10 5 5
1 1 5 10
Трамвайная линия имеет вид прямой. Петя живет в N трамвайных остановках от метро. Метро находится у нулевой остановки, в точке с координатой 0.
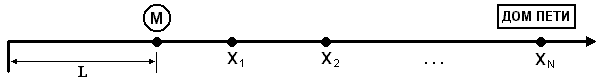
Выходя из метро, Петя хочет попасть домой как можно быстрее, но он очень не любит ждать трамвай на остановке. Поэтому, если, подходя к очередной трамвайной остановке, он не видит трамвая, то идет пешком вдоль трамвайной линии. Если в какой-то момент Петя видит трамвай, то он может принять решение вернуться на остановку, или продолжить свое движение к следующей остановке. Петя идет со скоростью U, трамвай едет со скоростью V. Нужно найти минимальное расстояние L, которое должно просматриваться перед нулевой остановкой, чтобы он мог идти со своей скоростью в сторону дома, не опасаясь, что трамвай его обгонит между остановками.
Во входном файле находятся три числа N, U и V (N ≤ 1000, U и V – положительные вещественные), за которым будет следовать N вещественных чисел – X1, X2,... Xn (0 < X1 < X2 < … < Xn < 106), разделенных пробелами.
В выходной файл ваша программа должна вывести число L с точностью до 10-4.
1 1 10 2
9.0000