Сортировка записей(9 задач)
Использование сортировки(13 задач)
Быстрая сортировка(55 задач)
Сортировка слиянием(9 задач)
Сортировка подсчетом(27 задач)
Сканирующая прямая(39 задач)
Сортировка событий(4 задач)
Вы когда-нибудь мечтали стать главным героем компьютерной игры? Главный герой этой истории, Бранимир, мечтает сейчас именно об этом.
Мир в мечте Бранимира состоит из N небоскребов, пронумерованных слева направо. Для i -го небоскреба, известна его высота H i и количество золотых монет G i на крыше этого небоскреба. Игра начинается с прыжка на любой из небоскребов и состоит из нескольких ходов. На каждом ходу Бранимир может прыгнуть на любой небоскрёб, находящийся справа от него, но так, чтобы высота нового небоскрёба была не меньше того небоскрёба, на котором сейчас сидит Бранимир. Оказавшись на крыше небоскреба, Бранимир собирает все золотые монеты на ней. Бранимир может закончить игру после любого количества шагов (возможно, нулевого), но он должен собрать не менее K золотых монет, чтобы перейти на следующий уровень.
Бранимир хочет узнать, сколько существует способов сыграть в эту игру так, чтобы перейти на следующий уровень. Две игры называются разными, если существует небоскреб который был посещен в одной игре, но не был посещён в другой.
Первая строка содержит 2 натуральных числа N и K ( 1 ≤ N ≤ 40 , 1 ≤ K ≤ 4·10 10 ) — число небоскрёбов и количество монет, которые надо набрать соответственно.
Следующие N строк содержат информацию о небоскрёбах. В i -й строке даны 2 числа H i и G i ( 1 ≤ H i , G i , ≤ 10 9 ) — высота и количество монет на i -м небоскрёбе.
В единственной строке вывода выведите число возможных игр, в которых Бранимир сможет пройти на следующий уровень.
Решение, корректно работающее при n ≤ 20 будет оцениваться в 40 баллов.
4 6 2 1 6 3 7 2 5 6
3
2 7 4 6 3 5
0
4 15 5 5 5 12 6 10 2 1
4
Петя увлёкся алгоритмами сжатия данных. Он уже изучил форматы gz , bz , zip и несколько других. Воодушевившись новыми знаниями, Петя собрался разработать свой формат сжатия и назвать его dis .
Петя решил сжимать таблицы. У него есть таблица, состоящая из n строк и m столбцов, заполненная целыми положительными числами. Он хочет заменить значения элементов таблицы на целые положительные числа так, чтобы отношение элементов в каждой строке и каждом столбце не изменилось. То есть, если в некоторой строке исходной таблицы a i , j < a i , k , то и в сжатой таблице a ' i , j < a ' i , k , и если a i , j = a i , k , то a ' i , j = a ' i , k . Аналогично, если в некотором столбце исходной таблицы a i , j < a p , j , то и в сжатой таблице a ' i , j < a ' p , j , и если a i , j = a p , j , то a ' i , j = a ' p , j .
Поскольку б'{о}льшие значения требуют больше места для хранения, максимальное значение элемента получившейся матрицы должно быть как можно меньше.
В теории Петя мастер, но вот писать код он не любит. Помогите ему реализовать формат сжатия dis .
В первой строке входных данных содержатся два числа
n
и
m
(
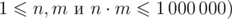 — количество строк и столбцов таблицы соответственно.
— количество строк и столбцов таблицы соответственно.
В следующих n строках содержится по m целых чисел a i , j (1 ≤ a i , j ≤ 10 9 ) — значения элементов таблицы.
Выведите сжатую таблицу: n строк, содержащих по m чисел.
Если существует несколько ответов, минимизирующих максимальное число, то разрешается вывести любой из них.
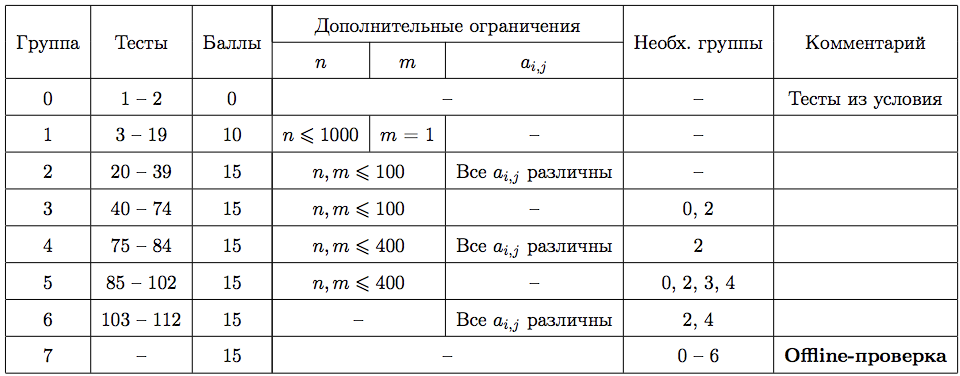
Тесты к этой задаче состоят из восьми групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых предыдущих групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.
В первом примере a 1, 2 ≠ a 2, 1 , но, поскольку они не располагаются в одной строке или в одном столбце, при сжатии их можно сделать равными.
2 2 1 2 3 4
1 2 2 3
4 3 20 10 30 50 40 30 50 60 70 90 80 70
2 1 3 5 4 3 5 6 7 9 8 7
Вы знаете, в чём разница между отелем и мотелем? Верно, разница в количестве мух, которые там живут. Норман – владелец одного из самых популярных мотелей в Америке,но его мать хочет, чтобы он стал отелем. Именно поэтому Норман купил мухобойку ( мухобойка – инструмент для отпугивания или прихлопывания мух. Может представлять собой как пластиковое или резиновое изделие на длинной ручке, так и пучок волос или листьев). Мухобойка представляет из себя многоугольник из \(\)\(K\)\(\) рёбер.
Желая угодить своей матери, Норман встал у окна, на котором сидели \(\)\(N\)\(\) мух. Так как норманн – пацифист, он не может причинить вред другому живому существу, в том числе, мухе. Именно поэтому ему интересно количество способов ударить по окну мухобойкой, не задев ни одной мухи.
Окно представляет из собой прямоугольник с левой нижней вершиной в точке \(\)\((0, 0)\)\(\) и правой верхней – в точке \(\)\((X_p, Y_p)\)\(\). После того как Норман ударит по окну все вершины многоугольника должны лежать в точках с целыми координатами, а мухобойка должна полностью лежать внутри прямоугольника окна. Норману интересно, сколькими способами он может ударить по окну, не убив ни единой мухи.
Первая строка содержит три числа \(\)\(X_p, Y_p, N\)\(\) (\(\)\(1 \leq X_p, Y_p \leq 500\)\(\), \(\)\(0 \leq N \leq X_p\cdot Y_p\)\(\)) — координаты верхней правой точки окна и количество мух на окне соответственно.
Следующие \(\)\(N\)\(\) строк содержат по \(\)\(2\)\(\) целых числа \(\)\(x_i, y_i\)\(\), задавая координаты мух на окне (\(\)\(0 < x < X_p\)\(\), \(\)\(0 < y_i < Y_p\)\(\)).
В следующей строке вводится одно число \(\)\(K\)\(\) (\(\)\(3 \leq K \leq 10\,000\)\(\)) — количество вершин многоугольника мухобойки. Следующие \(\)\(K\)\(\) строк содержат по два числа \(\)\(x_j, y_j\)\(\) (\(\)\(-10^9 \leq x_j, y_j \leq 10^9\)\(\)), задавая \(\)\(j\)\(\)-ю вершину многоугольника. Вершины многоугольника заданы в порядке обхода по или против часовой стрелке.
Выведите искомое число способов ударить по окну, не задев ни одной мухи.
Решение, правильно работающее на тестах, в которых \(\)\(1 \leq X_p, Y_p \leq 100\)\(\) будет оцениваться в \(\)\(62\)\(\) балла.
Пояснение к третьему примеру:
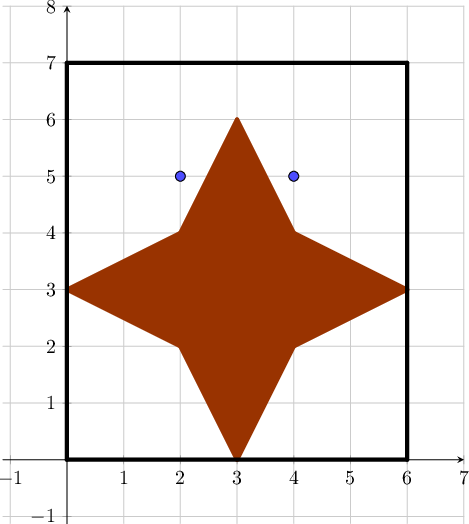
4 5 2 1 3 3 4 4 0 0 2 0 2 2 0 2
4
5 5 3 1 4 1 3 2 2 3 4 7 6 3 7 6
3
6 7 2 2 5 4 5 8 1 4 3 3 4 1 5 3 7 4 5 5 4 7 3 5
1
Теперь вас назначили управляющим одной телекоммуникационной компании. Вы отвечаете за обеспечение маленького городка контентом. Каждый дом задается его координатами на плоскости. Известно, что никакие три дома не лежат на одной прямой, а никакие четыре на одной окружности. Вы решили поставить одну антенну так, чтобы сигнал от нее был доступен домам в определенным радиусе, т.е. область, в которой доступен контент является кругом. Вы еще не очень разобрались в политике вашей компании, поэтому решили сделать не слишком сложный выбор данной области: вы просто выбираете 3 случайных дома и строите круг так, чтобы эти три дома были на его границе (вы ходили на геометрию в 7 классе и вам известно, что так всегда можно сделать). Теперь вам интересно, сколько в среднем домов будут иметь доступ к контенту. Выведите ответ с точностью до 4 знаков после запятой.
Первая строка входных данных содержит одно число \(3 \le n \le 1500\) - кол-во домов. Каждая из следующих \(n\) строк содержит два целых числа \(-10^6 \le x_i, y_i \le 10^6\) - координаты \(i\)-го дома.
Выведите одно число - ответ на задачу с точностью до 4 знаков после запятой.
Подзадача 1(40 баллов) \(1 \le n \le 100\)
Подзадача 2(30 баллов) \(1 \le n \le 500\)
Подзадача 3(30 баллов) \(1 \le n \le 1500\)
4 0 2 4 4 0 0 2 0
3.500000