Горнолыжник, готовясь к соревнованиям, нарисовал на бумаге схему горнолыжной трассы для выбора оптимального маршрута спуска. На схеме расположенные на трассе ворота представлены горизонтальными отрезками. Никакая пара ворот не имеет общих точек.
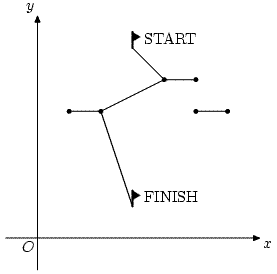
Маршрут должен представлять собой ломаную, начинающуюся в точке старта на вершине горы и заканчивающуюся в точке финиша у ее подножия. Маршрут выбирается таким образом, что y-координата каждой следующей вершины ломаной оказывается строго меньше y-координаты предыдущей вершины. Один из возможных маршрутов представлен на рисунке.
За каждые ворота, через которые не проходит маршрут, лыжнику начисляются штрафные очки. Общий штраф за спуск по маршруту вычисляется как сумма длины маршрута и штрафных очков за непройденные ворота.
Требуется написать программу, которая определяет, какой минимальный общий штраф горнолыжник может получить при прохождении трассы.
В первой строке входного файла задано число N - количество ворот на трассе (0 ≤ N ≤ 500), в следующих двух строках заданы Sx, Sy, Fx, Fy - координаты точек старта и финиша соответственно. В каждой из следующих N строк записаны четыре числа ai, bi, yi, ci - x-координаты левого и правого концов ворот, y-координата ворот и штраф за непрохождение данных ворот (ai < bi, Fy < yi < Sy, ci - целое число, 0 ≤ ci ≤ 10000). Все координаты - целые числа, не превосходящие по модулю 10000.
В выходной файл выведите наименьший возможный общий штраф за прохождение трассы с точностью не менее 4 знаков после десятичной точки.
Потестовая.
4 3 6 3 1 5 7 4 1 4 5 5 10 1 2 4 5 2 5 2 0
7.8126
Чтобы поднять в свой офис на N-м этаже небоскреба новый сейф, Вите опять пришлось прибегнуть к помощи грузчиков. Но за это время система оплаты изменилась. Теперь за подъем по лестнице на один этаж требуется заплатить U рублей, за спуск по лестнице на один этаж — D рублей, за внос в лифт — I рублей, за вынос из лифта — J рублей.
В офисе имеется L лифтов, каждый из которых останавливается лишь на определенных этажах.
Помогите Вите разработать маршрут подъема сейфа с первого этажа, стоимость которого наименьшая.
В первой строке входного файла записаны целые числа N, U, D, I, J, L. Каждая из следующих L строк описывает соответствующий лифт. Она начинается с числа Ki — количества этажей, на которых останавливается i-й лифт, за которым следует Ki натуральных чисел — этажи, на которых останавливается этот лифт (этажи для каждого лифта задаются в возрастающем порядке). 0≤U≤1000, 0≤D≤1000, 0≤I≤1000, 0≤J≤1000, 0≤L≤500, 1≤N≤1000000, 2≤Ki≤1000, K1+K2+…+KL≤100000. Количество этажей в небоскребе не превосходит 1000000.
В выходной файл выведите одно число — минимальную стоимость подъема сейфа.
Группы тестов:
10 1 1 1 1 1 2 3 7
7
10 1 1 3 2 1 2 3 7
9
20 100 0 1 1 2 2 5 7 2 8 17
804
См. «Двоичная куча (пирамида). Пирамидальная сортировка. Приоритетная очередь» (PDF), стр. 9, задача 1.
Ограничение времени – 2 секунды
См. «Двоичная куча (пирамида). Пирамидальная сортировка. Приоритетная очередь» (PDF), стр. 10, задача 2.
Ограничение времени – 2 секунды
См. «Двоичная куча (пирамида). Пирамидальная сортировка. Приоритетная очередь» (PDF), стр. 10, задача 3.
Ограничение времени – 1 секунда