Назовем число, записанное LED-цифрами, симметричным, если его запись обладает осевой симметрией с вертикальной либо горизонтальной осью. К примеру: 88 – симметричное, 87 – не симметричное, 1338 – симметричное, 258 – не симметричное, 582 – симметричное, 15821 – не симметричное и т.п. Вам даны два числа: A и B , A ≤ B . Найти количество симметричных чисел в отрезке [ A , B ] (включая A и B ).

В полутемной комнате Милан сел за стол и начал думать о возможных последствиях ядерной катастрофы в своем городе. Поскольку Милан - мэр города, он очень хорошо знаком с такими событиями.

А именно, он знает, что в его городе живет ровно \(N\) человек и каждый житель живет в своем собственном доме. Между \(M\) парами домов есть дороги, и для каждой дороги известно, сколько времени потребуется для ее прохождения. Наконец, Милан знает, в каких \(K\) домах есть атомные укрытия и сколько людей помещается в каждое укрытие. Учитывая все это, у Милана возникает следующий вопрос: «Сколько времени нужно, чтобы эвакуировать всех жителей города?»

Помогите Милану ответить на этот вопрос.

Конечно, эвакуация означает, что каждый житель попадает в какое-то атомное убежище. Можно предположить, что жители двигаются оптимально (по кратчайшему пути) и что несколько человек могут двигаться по одной дороге одновременно, возможно в разных направлениях. Также можно считать, что между любыми двумя домами есть хотя бы один путь, проходящий по дорогам.

Город Загреб решил построить новую парковку. Для этого было решено использовать прямоугольный участок земли, который можно представить в виде матрицы с \(N\) строками и \(M\) столбцами. Чтобы привлечь гостей и увеличить доходы, мэр решил разместить фонтаны на заранее определенных участках земли. Остальные же клетки будут преобразованы в парковочные места и дороги. Машины могут двигаться по парковке, перемещаясь в соседнее поле в одном из четырех направлений (север, юг, восток или запад). При этом парковочные места должны быть выбраны так, чтобы любая припаркованная машина могла выехать из парковки, то есть иметь возможность попасть в левую верхнюю клетку, не врезаясь в другие припаркованные машины.

Помогите мэру и определите максимально возможное количество парковочных мест для данного участка.

Король Байтазар считает, что Байтотия — земля, полная красивых достопримечательностей — должна привлечь множество туристов, которые должны потратить много денег, которые в конечном счете должны найти свой путь в королевскую казну. Но реальность далека от мечты. Поэтому король поручил своему советнику изучить этот вопрос. Советник выяснило, что иностранцы держаться подальше от Байтотии из-за ее плохой дорожной сети. В Байтотии \(n\) городов соединенных \(m\) двусторонними дорогами. Не гарантируется, что от каждого города можно добраться от любого другого города. Советник отметил, что нынешний дорожная сеть не позволяет делать длительные путешествия. А именно, где бы вы не начали поездку, невозможно посетить более 10 городов не прохождения через какой-то город два раза. Из-за ограниченных средств в казне, новые дороги построить нельзя. Вместо этого, Байтазар решил создать сеть туристическо-информационных пунктов (ТИП), которые будут рекламировать короткие путешествия. Для каждого города должен быть ТИП либо в нем, либо в одном из городов, непосредственно связанных с ним дорогой. Кроме того, известна стоимость строительства ТИПа в каждом из городов. Помогите королю найти самый дешевый спосою построить ТИПы, так, чтобы это условие удовлетворялось.

Центр Гдынии расположен на острове посередине реки Кацза. Каждое утро тысячи машин едут из жилых районов на западном берегу в индустриальные на восточном.

Остров можно представить в виде прямоугольника \(A\times B\) со сторонами, параллельными осям координат, углами \((0, 0)\) и \((A, B)\).

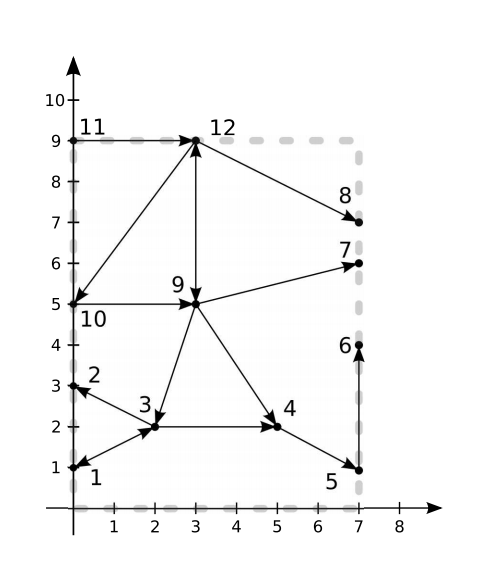
На острове есть \(n\) перекрёстков, пронумерованных натуральными числами от \(1\) до \(n\). Перекрёсток номер \(i\) имеет координаты \((x_i, y_i)\). Если координаты какого-то перекрёстка имеют вид \((0, y)\), то он находится на западном берегу, если \((A, y)\) - на восточном. Перекрёстки соединены дорогами, каждая - отрезок на плоскости, они не пересекаются (кроме концов). Дороги бывают односторонними и двусторонними. Нет никаких мостов и туннелей! Некоторые дороги могут идти по краям прямоугольника.

Поскольку плотность траффика растёт, мэр города нанял Вас (кого же ещё) проверить, достаточно ли текущей сети дорог. Он попросил написать программу, которая по карте города определит для каждого перекрёстка на западном берегу, сколько из него достижимых на восточном.