Улица М. города Д. печально известна среди местных жителей качеством дорожного покрытия. В этом тяжело винить ремонтные службы: пожалуй, они следят за этой улицей даже слишком тщательно. Проблема в том, что каждый без исключения ремонт улицы выглядит следующим образом: бригада рабочих выбирает некоторый участок улицы единичной длины и меняет асфальт только на нём, причём тип асфальта на этом участке в результате может отличаться от типов асфальта на других участках, что, разумеется, усложняет проезд по улице.

Вы, как коренной житель города Д. и программист по призванию, решили использовать свои профессиональные навыки на благо общества и облегчить жизнь своим соседям по улице \(М\). А именно, вы решили создать сайт, содержащий актуальную информацию о непроходимости улицы. Прежде всего, вы заметили, что улица разбита на N идущих друг за другом участков единичной длины. По странному совпадению бригада рабочих всегда выбирает для ремонта ровно один из таких участков и целиком меняет тип асфальта на нём. Затем вы пронумеровали эти участки от 1 до \(N\) и собрали информацию о типе асфальта на каждом из участков — числа \(t_1, t_2, ... , t_N\) (\(t_i\) — номер типа асфальта на \(i\)-м участке, согласно Государственному реестру дорожных покрытий). Наконец, вы определили непроходимость улицы как минимальное количество непрерывных непересекающихся отрезков c одинаковым типом асфальта, на которые она разбивается. Например, непроходимость улицы 110111 равна \(3\), потому что она состоит из трёх участков 11, 0 и 111, а идеальная улица 2222 имеет непроходимость, равную \(1\).

Казалось бы, достаточно вычислить и разместить на сайте текущую величину непроходимости улицы, и жители будут довольны? К сожалению, асфальт меняют довольно часто, и вам не хочется каждый раз выходить на улицу и заново собирать данные. Поэтому вы дали возможность жителям сообщать на вашем сайте об обновлении дорожного покрытия. Дело осталось за малым — научиться обновлять после каждого такого сообщения актуальную величину непроходимости улицы.

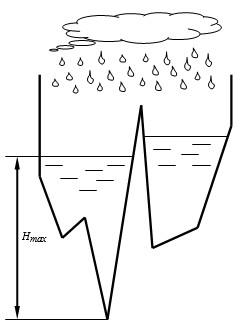
В НИИ метеорологии решили изучить процесс образования водоемов на различных рельефах местности во время дождя. Ввиду сложности реальной задачи была создана двумерная модель, в которой местность имеет только два измерения — высоту и длину. В этой модели рельеф местности можно представить как N-звенную ломаную c вершинами \((x_0, y_0), ..., (x_N, y_N)\), где \(x_0 < x_1 < ... < x_N\) и \(y_i \neq y_j\), для любых \(i \neq j\). Слева в точке \(x_0\) и справа в точке \(x_N\) рельеф ограничен вертикальными горами огромной высоты.

Если бы рельеф был горизонтальным, то после дождя вся местность покрылась бы слоем воды глубины H. Но поскольку рельеф — это ломаная, то вода стекает и скапливается в углублениях, образуя водоемы.

Требуется найти максимальную глубину в образовавшихся после дождя водоемах.

В Берляндии по воскресеньям проходит известое шоу — игра «Слабое звено».

В игре принимают участие \(n\) игроков, которые выстраиваются в круг. Каждому игроку сопоставлен рейтинг — некоторое целое число \(a_i\).

Игра проходит в несколько раундов, каждый из которых выглядит следующим образом:

• В очередном раунде принимают участие все ещё не выбывшие игроки.

• Все игроки, которые по рейтингу строго слабее обоих своих соседей по кругу, объявляются слабым звеном и выбывают из игры.

• Все оставшиеся участники сдвигаются чуть плотнее, чтобы снова образовывать круг.

• Игра заканчивается, если после очередного раунда осталось ровно два человека или если после очередного раунда не выбыл ни один человек.

• Иначе начинается новый раунд.

Можно показать, что если до очередного раунда в игре оставалось хотя бы три участника, то после одного раунда гарантированно останется не менее двух участников.

Вам нужно выяснить для каждого участника, останется ли он до конца, или номер раунда, в котором он покинет игру.