Системы счисления(36 задач)
"Длинная" арифметика(58 задач)
Простые числа и разложение на множители(45 задач)
Остатки(21 задач)
Быстрое возведение в степень(3 задач)
Быстрое преобразование Фурье(3 задач)
Дано натуральное число N. Требуется написать программу, которая находит такое минимальное число M, произведение цифр которого равно N.
Вводится целое число N (1 ≤ N ≤ 2·106) .
Выведите на экран одно число M ≥ 10 или фразу «No solution». Число M должно начинаться со значащей цифры (не с нуля).
20
45
1
11
В фирме, в которой работает ваш друг, ввели новый дизайн билетов на маршрутки. Теперь номер билета может быть любым натуральным числом. Радостные пассажиры тут же придумали новый, очень простой способ определения счастливости номера билета. Он состоит в следующем. Пусть номер билета равен \(N\). Если \(N<10\), то счастливость числа \(N\) (т.е. и самого билета) равна \(N\), иначе: посчитаем сумму цифр числа \(N\), пусть она равна \(S\) — тогда счастливость числа \(N\) будет равна счастливости числа \(S\).
Например, счастливость билета с номером \(7351\) равна счастливости билета с номером \(16\) (т.к. \(7+3+5+1=16\)), а она в свою очередь равна счастливости билета с номером 7 (т.к. \(1+6=7\)), а последняя просто равна 7 (т.к. \(7<10\)).
Такое определение счастливости вполне устроило обычных пассажиров маршрутки, но совсем не устроило большинство студентов, которые быстро нашли способ без особенных усилий определять счастливость билета. Поэтому, используя это определение, они придумали новую игру: обладатель билета должен разложить его номер в сумму нескольких чисел так, чтобы суммарная счастливость слагаемых была максимальна.
Но и эта игра устроила не всех студентов. Наиболее активные из них заметили, что игра становится ещё более интересной, если раскладывать \(N\) не в сумму, а в произведение чисел, с целью, по-прежнему, максимизировать сумму счастливостей множителей.
Напишите программу, которая будет решать эту задачу, т.е. по данному \(N\) находить такое его представление \(N=a_1\cdot a_2\cdot \ldots\), где все \(a_i\) натуральны, больше единицы, и суммарная счастливость чисел \(a_1\), \(a_2\), ... максимальна.
Для вашего удобства номер билета \(N\) задан его разложением на простые множители. Таким образом, первая строка входного файла содержит одно натуральное число — количество множителей в разложении числа \(N\) на простые, а далее следуют сами множители. \(N\) не превосходит \(10^{18}\), а каждый простой множитель не превосходит \(10^9\).
Если оптимальных решений несколько, выведите любое.
В выходной файл выведите искомое разложение \(N\) на множители. А именно, сначала выведите количество множителей в вашем разложении, а потом — сами множители.
Если ваша программа будет проходить тесты, в которых \(N\leq 10^9\), то она получит не менее 30 баллов.
3 2 2 3
2 6 2
2 2 11
2 2 11
Вчера у Васи был счастливый день: он наконец дописал программу всей своей жизни! И, недолго думая, он тут же запустил ее на Самом Главном Тесте.
Программа Васи очень сложная, и потому работает она долго. Поэтому Вася пошел спать, а наутро, сегодня, обнаружил, что программа, вместо того, чтобы посчитать нужный Ответ, вылетела с непонятной ошибкой.
Вася понял, что напрасно он не тестировал программу. Ведь Самый Главный Тест очень сложный — в нем есть \(N\) отдельных подзадач, и каждую из них надо решить. Конечно, надо было бы начать тестирование с меньшего количества подзадач, но ведь Вася — очень умный программист! И он абсолютно уверен, что его программа корректно решила все подзадачи, кроме какой-то одной. Вот только Вася не знает, какой именно.
Вася может изменять Самый Главный Тест, отключая в нем те или иные подзадачи. Он надеется, что, если среди отключенных будет та подзадача, на которой его программа не работает, то получившийся тест его программа спокойно пройдет. Но вот проблема: программа работает долго, а подзадач много, и потому, если отключать задачи по одной, то придется очень долго искать нужную. А Вася очень хочет узнать, где ошибка, уже завтра!
К счастью, у Васи в распоряжении есть много компьютеров. Он может на некоторых из них запустить свою программу на каком-то тесте (т.е. на Самом Главном Тесте с некоторыми отключенными подзадачами), а назавтра посмотреть, какие программы завершились успешно, а какие нет, — и по результатам понять, какая подзадача создавала проблемы. Помогите Васе подобрать тесты для каждого из компьютеров, т.е. объясните ему, какие подзадачи в каком тесте он должен отключить, так, чтобы назавтра, узнав результаты работы программы на этих тестах, он смог бы уверенно определить, с какой подзадачей у него возникают проблемы (естественно, считая, что такая подзадача только одна, ведь Вася — очень умный программист!)
Учтите, что Васе не хочется делать лишнюю работу по запуску программ и определению их результата, поэтому он хочет минимизировать количество запусков (т.е. фактически количество компьютеров, ведь его программа настолько сложная, что на одном компьютере можно запустить только один экземпляр программы).
В первой и единственной строке входного файла находится одно целое число \(N\) — количество подзадач в Самом Главном Тесте (\(1 \le N \le 10^5\)).
В первой строке выходного файла выведите минимальное необходимое количество компьютеров \(M\). В последующих \(M\) строках выведите информацию о том, на каком тесте надо запускать программу на каком компьютере. А именно, в \(i\)-ую из них выведите последовательность чисел \(k_i\), \(b_{i1}\), \(b_{i2}\), ...., \(b_{ik_i}\), где \(k_i\) — количество подзадач, которые надо отключить в тесте, на котором будет работать программа на \(i\)-ом компьютере, а \(b_{ij}\) (\(1 \le j \le k_i\), \(1 \le b_{ij} \le N\)) — номера подзадач, которые надо отключать. Числа \(b_{ij}\) должны быть различны для каждого фиксированного \(i\).
Подзадачи нумеруются от 1 до \(N\).
В пределах одной строки подзадачи можете выводить в любом порядке. Если есть несколько оптимальных решений, выведите любое.
В примере:
5
3 3 1 3 5 3 1 2 5 4 1 2 3 4
В факториальной системе счисления основаниями являются последовательность факториалов bk = k!, и каждое натуральное число x представляется в виде:
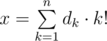 , где 0 ≤ dk ≤ k
, где 0 ≤ dk ≤ k Ваша задача определить по данному в факториальной системе счисления числу его остаток от деления на p.
В первой строке даны два натуральных числа n и p, где n - максимальный индекс такой, что dn ≠ 0 (1 ≤ n ≤ 200, 2 ≤ p ≤ 104). Во второй строке задана последовательность dn, ..., d1, корректно определяющая некоторое натуральное число x.
Выведите одно число — остаток от деления x на p.
5 6
1 3 3 2 1
5
В исходном примере x = 215
Числа Фибоначчи - элементы числовой последовательности, в которой каждое последующее число равно сумме двух предыдущих чисел. Более формально, последовательность чисел Фибоначчи {Fn} задается линейным рекуррентным соотношением:
Рассмотрим систему счисления с двумя цифрами 0 и 1, в которой, в отличие от двоичной системы весами являются не степени двойки 1,2,4,8,16,..., а числа Фибоначчи 1,2,3,5,8,13,.... В этой системе счисления каждое положительное целое число единственным образом представляется в виде строки нулей и единиц, которая начинается с 1 и в которой нет двух единиц, стоящих рядом.
Даны две строки, представляющие натуральные числа A и B. Найти строку, представляющую число A+B.
Даны две строки, представляющие A и B, состоящие из нулей и единиц. Длина каждой из строк не превышает 104.
Выведите строку, представляющую число A + B. Обратите внимание, что она должна начинаться с единицы.
10101
100
100010
Исходные строки '10101' и '100' представляют числа 8 + 3 + 1 = 12 и 3. Ответом является строка '100010', представляющая строку 13 + 2 = 15 = 12 + 3.