--->
45 задач
<---
Источники
#111286
Темы:
[НОД и алгоритм Евклида]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Сегодня на уроке математики шестиклассник Петя изучил понятие наибольшего общего делителя. Петя тут же решил применить полученные знания на практике.
Петя выписал на листке бумаги \(n\) чисел \(a_1, \ldots, a_n\) --- номера домов, в которых живут его друзья. Теперь он хочет выбрать такое подмножество этих чисел, чтобы их наибольший общий делитель был равен его любимому числу \(d\).
Помогите Пете выбрать из выписанных чисел искомое подмножество.
Входные данные
Первая строка входного файла содержит два целых числа \(n\) и \(d\) (\(1 \le n \le 1000\), \(1 \le d \le 10^9\)). Вторая строка содержит \(n\) целых чисел: \(a_1, a_2, \ldots, a_n\) (\(1 \le a_i \le 10^9\)).
Выходные данные
Если существует искомое подмножество, выведите на первой строке выходного файла число \(k\) --- количество чисел в нем. На второй строке выведите числа, входящие в это подмножество.
Если решения не существует, выведите на первой строке выходного файла число \(-1\).
Если возможных ответов несколько, выведите любой из них.
Примеры тестов
Входные данные
4 3 6 8 12 9
Выходные данные
2 6 9
Входные данные
3 3 2 4 8
Выходные данные
-1
Известно, что запись числа A в позиционных системах счисления с основанием p и q имеет вид бесконечной периодической дроби с периодом 2:
Написать программу, которая для введенных натуральных чисел p и q находит и выводит все возможные пары значений цифр a и b, удовлетворяющих соотношению ( * ).
Входные данные
Даны два числа p и q (2 ≤ p < q ≤ 105).
Выходные данные
В первой строке выведите число k — количество пар a и b. Далее в n строках выведите эти пары (a < b). Пары следует выводить в порядке возрастания a, а если они равны, то в порядке возрастания b. Если пар нет, то k должно быть равно 0.
Примеры тестов
Входные данные
5 11
Выходные данные
1
1 4
Примечание
Значением числа, запись которого в позиционной системе счисления с основанием s есть 0, cdef (где c, d, e, f - цифры), является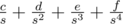 
Определим множества K[i] рекуррентно. Пусть K[0] = [0, 1]. Разделим сегмент [0, 1] на три части точками 
и 
и удалим из него интервал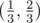 
. Получим множество K[1], состоящее из двух оставшихся сегментов 
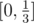и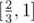 
.
Каждый из них разделим на три части (точками 
и 
для первого сегмента, и точками 
и 
- для второго) и удалим средние интервалы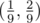 
и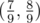 
. Таким образом получаем множество K[2], и т.д.
Пусть мы построим множество K[i]. Поделим каждый оставшийся сегмент из K[i] на 3 части и удалим из этих сегментов средние интервалы. Получим, таким образом, из K[i] множество K[i + 1].
Вводятся 3 целых числа n, a, b. Необходимо определить, принадлежит ли точка с координатой 
множеству K[n].
Входные данные
Даны три натуральных числа n, a, b (1 ≤ n ≤ 106, 0 ≤ a ≤ b ≤ 1018, b ≠ 0).
Выходные данные
Выведите «YES» в случае, если точка принадлежит множеству K[n]. Иначе — выведите «NO».
Примеры тестов
Входные данные
1 2 4
Выходные данные
NO
Входные данные
2 13 18
Выходные данные
YES
Заданы натуральные числа e, k, m, t в записи химической реакции
Входные данные
Даны четыре натуральных числа (1 ≤ e, k, m, t ≤ 109)
Выходные данные
Выведите четыре числа — коэффициенты перед слагаемыми уравнения в порядке слева направо.
Примеры тестов
Входные данные
2 3 5 6
Выходные данные
2 5 1 4
Примечание
Исходный пример соответствует уравнению 2X2A3 + 5Y = Y5A6 + 4X
Вводятся целые числа a и b. Пусть у треугольника ABC координаты A = (0, 0), B = (a, b), а обе координаты C = (x, y) - целые числа, и площадь треугольника ABC не равна нулю.
Какую минимальную площадь может иметь треугольник ABC?
Входные данные
Даны два целых числа a и b, по модулю не превосходящие 109. (a2 + b2 > 0)
Выходные данные
Выведите одно число — минимальную возможную площадь треугольника ABC с точностью 10 - 9. То есть ответ будет считаться правильным, если будет отличаться от ответа жюри менее, чем на 10 - 9
Примеры тестов
Входные данные
4 0
Выходные данные
2.0
Выбрано
:
|