Перебор с отсечением(22 задач)
Простые задачи на перебор(43 задач)
Гамильтонов цикл(2 задач)
Натуральное число \(a\) называется делителем натурального числа \(b\), если \(b = ac\) для некоторого натурального числа \(c\). Например, делителями числа 6 являются числа 1, 2, 3 и 6. Два числа называются взаимно простыми, если у них нет общих делителей кроме 1. Например, 16 и 27 взаимно просты, а 18 и 24 — нет.
Будем называть нормальным набор из \(k\) чисел (\(a_1, a_2, \ldots, a_k\)), если выполнены следующие условия:
Например, набор (2, 9, 10) является нормальным набором из 3 делителей числа 360.
Требуется написать программу, которая по заданным значениям \(n\) и \(k\) определяет количество нормальных наборов из \(k\) делителей числа \(n\).
Первая строка входного файла содержит два целых числа: \(n\) и \(k\) (\(2 \le n \le 10^8\), \(2 \le k \le 10\)).
В выходном файле должно содержаться одно число — количество нормальных наборов из \(k\) делителей числа \(n\).
Правильные решения для тестов, в которых \(n \le 1000\) и \(k = 2\), оцениваются из 30 баллов.
Правильные решения для тестов, в которых \(k = 2\), оцениваются из 60 баллов (в эти баллы включаются также 30 баллов для случая \(n \le 1000\), \(k = 2\)).
90 3
16
10 2
4
Рассматриваются все разбиения натурального числа \(N\) на сумму \(К\) неотрицательных слагаемых (\(1 \leq N \leq 32\), \(2 \leq K \leq 32\)). Суммы, отличающиеся только порядком слагаемых, считаем различными. Упорядочим все разбиения по убыванию первого слагаемого, а при равных первых слагаемых – по убыванию второго слагаемого, а при равных первых и вторых слагаемых – по убыванию третьего слагаемого и т. д. Пронумеруем их. Например, при \(N=4\), \(К=3\) имеем:
| Номер | 1 слагаемое | 2 слагаемое | 3 слагаемое |
|---|---|---|---|
| 1 | 4 | 0 | 0 |
| 2 | 3 | 1 | 0 |
| 3 | 3 | 0 | 1 |
| 4 | 2 | 2 | 0 |
| 5 | 2 | 1 | 1 |
| 6 | 2 | 0 | 2 |
| 7 | 1 | 3 | 0 |
| 8 | 1 | 2 | 1 |
| 9 | 1 | 1 | 2 |
| 10 | 1 | 0 | 3 |
| 11 | 0 | 4 | 0 |
| 12 | 0 | 3 | 1 |
| 13 | 0 | 2 | 2 |
| 14 | 0 | 1 | 3 |
| 15 | 0 | 0 | 4 |
В первой строке входного файла записана последовательность чисел. Если первое число \(0\), то необходимо найти разбиение по номеру, а если \(1\), то номер по разбиению. В первом случае далее в файле записано количество слагаемых, сумма и номер разбиения. Во втором случае далее в файле записано количество слагаемых \(K\) и затем разбиение (\(K\) неотрицательных чисел, сумма которых \(N\)). Все числа разделены пробелами.
Выведите в выходной файл разбиение либо номер.
0 3 4 9
1 1 2
1 3 0 1 3
14
В парке растут два очень высоких дерева, на стволе каждого из которых расположены дупла одно под другим на равном расстоянии друг от друга. Однажды N дятлов решили заселить эти дупла. Некоторые из них знакомы и поэтому хотели бы иметь возможность летать друг к другу в гости. Дятлы летают прямолинейно и очень быстро. Чтобы уменьшить вероятность столкновения, они решили селиться по следующему принципу:
Каждые две дятла, которые хотят летать друг к другу в гости, должны жить на разных деревьях Отрезки, соединяющие дупла знакомых между собой дятлов не пересекаются (однако их концы могут совпадать).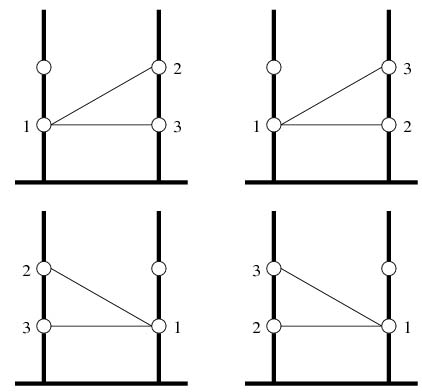 Кроме того, дятлы хотят жить как можно ниже, т.е. на каждом из деревьев они занимают дупла подряд, начина снизу. На каждом из деревьев больше дупел, чем общее количество дятлов.
Кроме того, дятлы хотят жить как можно ниже, т.е. на каждом из деревьев они занимают дупла подряд, начина снизу. На каждом из деревьев больше дупел, чем общее количество дятлов.В первой строке содержатся три числа: \(N\) – количество дятлов (\(1 \leq N \leq 10^6\)), \(M\) – количество пар знакомых дятлов (\(1 \leq M \leq 10^7\)) и число \(K\) (\(1 \leq K \leq 2\times 10^6\)). Дятлы занумерованы от \(1\) до \(N\). В следующих \(M\) строках заданы два числа \(a_i\) и \(b_i\) (\(1 \leq a_i, b_i \leq N\)), задающие пару знакомых дятлов.
Вывод должен содержать одно число: количество вариантов размещения по модулю K.
3 2 10 1 2 1 3
4
4 4 17 1 2 1 3 4 2 3 4
0
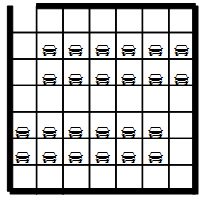
Автостоянка в Цветочном городе представляет собой прямоугольник \(N\times M\) клеток, в каждую из которых можно поставить машину. Стоянка обнесена забором, одна из сторон угловой клетки удалена (это ворота). Машина ездит по дорожке шириной в одну клетку. Незнайку попросили разместить как можно больше машин на стоянке таким образом, чтобы любая машина могла выехать, когда все прочие стоят. Например, на рисунке справа показано, как можно расположить 24 машины на стоянке размером \(7\times 7\). Помогите Незнайке решить эту задачу.
Во входном файле записано два натуральных числа N и M, не превосходящие 7.
Выведите в выходной файл единственное число: максимальное количество машинок, которое можно расставить на стоянке данного размера.
1 3
1
2 2
2
Во входном файле заданы неотрицательные целые числа \(n\) и \(m\), не превосходящие 400000.
Выведите ответ на задачу в десятичной системе счисления без ведущих нулей.
7 7
3432
4 1
5