Интернациональная Развлекательная Компания только что выпустила новую машину со слотами. Она состоит из круглых слотов одинакового размера, расположенных в виде треугольника. Пример с четырьмя рядами показан ниже. Когда игрок нажимает рычаг, машина выводит по произвольной букве в каждый слот. Если после этого некоторые три одинаковые буквы оказываются в вершинах правильного треугольника, то машина выдает деньги. В приведенном примере буквы 'а' и 'с' удовлетворяют условию.
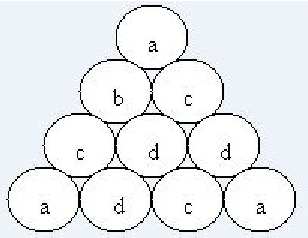
Компания выпускает несколько моделей машины, различающиеся количеством рядов слотов. Но возникли трудности с написанием программы, определяющей выигрышную позицию. В этом и состоит ваша задача.
Входные данные состоят из набора нескольких тестов. Каждый тест начинается с натурального числа N, показывающего количество рядов в машине. Следующая строка состоит из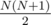 
алфавитных маленьких букв, которые будут загружены построчно в машину, начиная с вершины. Например, то, что показано на рисунке описывается так: 4 abccddadca Значение N не более 12. Строка с одиночным нулем завершает ввод.
Для каждого варианта входных данных выведите буквы, образующие равносторонний треугольник в алфавитном порядке. Если таких букв нет, выведите «LOOOOOOOOSER!».
4 abccddadca 6 azdefccrhijrrmznzocpq 2 abc 0
ac crz LOOOOOOOOSER!
Биологи Карельского Мутационного Проекта (КМП) недавно решили начать новые исследования, которые должны доказать, что люди — близкие родственники мамонтов. Чтобы доказать это странное предположение, ученые планируют сравнить ДНК людей и мамонтов.
Для сравнения ДНК разделяется на фрагменты длины n и они последовательно сравниваются. Поскольку в процессе развития у людей и мамонтов могли происходить мутации, предлагается следующий способ сравнения фрагментов.
Рассмотрим строку α. Будем говорить, что α мутирует в β, если α = xyz для некоторых (возможно пустых) x, y и z, а β = xyRz, где yR означает строку y, записанную задом наперед (например, "abc"R = "cba"). Будем говорить, что строки α и β похожи, если α может быть превращена в β не более чем за 4 мутации.
По двум данным фрагментам ДНК определите, похожи ли они.
Входной файл содержит две строки, состоящие из символов 'A', 'D', 'G' и 'T'. Строки имеют одинаковую длину, не превышающую 30.
Выведите в выходной файл "Similar", если строки похожи, и "Different", если нет.
В первом примере возможна следующая последовательность мутаций: "ATGAATGA", "AGTAAGTA", "AGGAATTA".
ATGAATGA AGGAATTA
Similar
ATGAATGAATGA TTTAAAAAAGGG
Different
У Пети имеется игровое поле размером \(3\times3\), заполненное числами от 1 до 9. В начале игры он может поставить фишку в любую клетку поля. На каждом шаге игры разрешается перемещать фишку в любую соседнюю по стороне клетку, но не разрешается посещать одну и ту же клетку дважды. Петя внимательно ведет протокол игры, записывая в него цифры в том порядке, в котором фишка посещала клетки. Пете стало интересно, какое максимальное число он может получить в протоколе. Помогите ему ответить на этот вопрос.
Входной файл содержит описание поля — 3 строки по 3 целых числа, разделенных пробелами. Гарантируется, что все девять чисел различны и лежат в диапазоне от 1 до 9.
Выведите одно целое число — максимальное число, которое могло получиться в протоколе при игре на данном поле.
Ответ можно выводить не в виде числа, а в виде строки или в виде последовательности отдельных цифр (но не разделяя их пробелами).
| Ввод | Вывод |
|---|---|
1 2 3 |
987456321 |
На день рождения Егору подарили волшебный квадрат.
Волшебный квадрат — это таблица 3 × 3, в каждой из ячеек которой находятся числа от 0 до 9. Егор придумал следующую игру с волшебным квадратом: он загадывает число N и пытается так поставить числа в каждую ячейку квадрата, чтобы сумма чисел в каждой строке и каждом столбце была равна в точности N.
Пусть расстановка — это волшебный квадрат, заполненный числами. Тогда расстановки A и B считаются различными, если хотя бы для каких-то строки x и столбца y выполняется неравенство Ax, y ≠ Bx, y, где Ax, y и Bx, y — это числа, находящиеся в строке x и столбце y в расстановках A и B соответственно.
Егор задумался, сколько всего существует различных расстановок таких, что сумма в каждой строке и в каждом столбце была равна в точности N.
Напишите программу, которая поможет ответить на вопрос Егора.
Единственная строка входных данных содержит целое число N (0 ≤ N ≤ 109).
Требуется вывести одно число — искомое количество расстановок.
0
1
В примере из условия существует всего одна допустимая расстановка — это таблица 3 × 3, состоящая из нулей. Очевидно, что сумма элементов в любой строке или столбце в такой расстановке равна 0.
На отдыхе в Теплой Стране Вера познакомилась с симпатичным волейболистом- трактористом Петром. Турист Петр, кстати, собирается после отличного отдыха в Теплой Стране отправиться в путешествие по городам Европы. Как известно, Европа обладает развитой транспортной системой: в Европе есть \(V\) интересующих Петра городов и \(E\) маршрутов ночных поездов. Каждый маршрут соединяет два различных города, время в пути составляет одну ночь. Поезда по маршруту ходят в обоих направлениях.
Основной целью поездки Петра является осмотр местных достопримечательностей. По- скольку Петр — невероятно занятой человек, то он решил, что все путешествие должно занимать не более четырех дней. Петр уже многое повидал, поэтому на осмотр достопримечательностей в каждом городе Петр тратит ровно один день. Он хочет составить наиболее практичный тур: каждый день он будет тратить на осмотр города, а каждую ночь — на переезд ночным поездом между городами. Разумеется, Петр не имеет ни малейшего желания посещать один город несколько раз.
Но на этом прагматичность Петра не заканчивается: Петр, как настоящий турист, хочет посмотреть на самые красивые европейские достопримечательности. Он долго изучал справочники и для каждого города оценил свою ожидаемую радость от его посещения \(p_i\). Теперь он хочет найти маршрут, при котором его радость будет наибольшей. Помогите Петру найти такой маршрут.
В первой строке входных данных заданы два целых числа \(V\) и \(E\) (1 ≤ \(V\); \(E \le 3*10^5\)) — количество городов и маршрутов поездов, соответственно. В следующей строке заданы V целых чисел \(p_i\) (1 ≤ \(p_i\) ≤ \(10^8\)), где \(p_i\) обозначает ожидаемую радость от посещения го- рода с номером \(i\). В следующих \(E\) строках заданы описания маршрутов поездов. Каждое описание состоит из пары различных чисел \(a_i\) и \(b_i\) (1 ≤ \(a_i\); \(b_i\) ≤ V\( \)) — номеров городов, между которыми курсирует этот маршрут поезда. Гарантируется, что между каждой парой городов существует не более одного маршрута поезда.
В первой строке выходных данных выведите число K (1 ≤ K ≤ 4) — количество городов в оптимальном маршруте туриста Петра. В следующей строке выведите номера этих городов в порядке посещения. Города нумеруются начиная с единицы. Если оптимальных маршрутов несколько, выведите любой из них.
Тесты к этой задаче состоят из пяти групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.
0. Тесты 1–2. Тесты из условия, оцениваются в ноль баллов.
1. Тесты 3–16. В тестах этой группы \(V\); \(E\) ≤ 100. Эта группа оценивается в 20 баллов
2. Тесты 17–32. В тестах этой группы \(V\); \(E\) ≤ 1 000. Эта группа оценивается в 20 баллов.
3. Тесты 33–53. В тестах этой группы \(V\) ≤ 3 000, \(E\) ≤ 60 000. Эта группа оценивается в 30 баллов.
4. В тестах этой группы дополнительные ограничения отсутствуют. Эта группа оценивается в 30 баллов. Решение будет тестироваться на тестах этой группы offline, т. е. после окончания тура.
5 4 4 2 3 1 5 1 2 2 3 3 4 4 5
4 2 3 4 5
4 3 1 2 3 4 1 2 1 3 1 4
3 4 1 3