Темы --> Информатика --> Алгоритмы --> Перебор --> Комбинаторные структуры
    Размещения с повторениями(11 задач)
    Перестановки(20 задач)
    Сочетания(5 задач)
    Разбиения(9 задач)
    Разные комбинаторные структуры(17 задач)
    Генерация по номеру(2 задач)
---> 59 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 6 7 8 9 10 11 12 >> Отображать по:
#3366
Дятлы
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Необходимо проверить отсутствие циклов

В парке растут два очень высоких дерева, на стволе каждого из которых расположены дупла одно под другим на равном расстоянии друг от друга. Однажды N дятлов решили заселить эти дупла. Некоторые из них знакомы и поэтому хотели бы иметь возможность летать друг к другу в гости. Дятлы летают прямолинейно и очень быстро. Чтобы уменьшить вероятность столкновения, они решили селиться по следующему принципу:

Каждые две дятла, которые хотят летать друг к другу в гости, должны жить на разных деревьях Отрезки, соединяющие дупла знакомых между собой дятлов не пересекаются (однако их концы могут совпадать).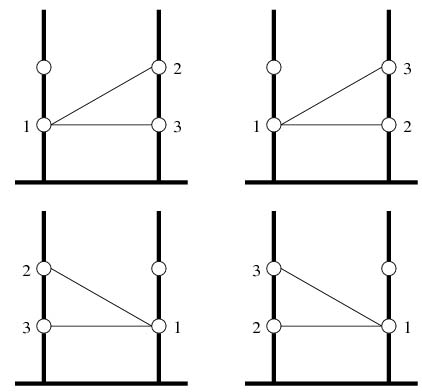

Кроме того, дятлы хотят жить как можно ниже, т.е. на каждом из деревьев они занимают дупла подряд, начина снизу. На каждом из деревьев больше дупел, чем общее количество дятлов.
Как известно, у дятлов очень маленький мозг. Поэтому вам следует подумать за них и сообщить, сколькими способами они могут разместиться в дуплах. Т.к. дятлы также плохо воспринимают большие числа, ответ следует вывести по модулю K.

Входные данные

В первой строке содержатся три числа: \(N\) – количество дятлов (\(1 \leq N \leq 10^6\)), \(M\) – количество пар знакомых дятлов (\(1 \leq M \leq 10^7\)) и число \(K\) (\(1 \leq K \leq 2\times 10^6\)). Дятлы занумерованы от \(1\) до \(N\). В следующих \(M\) строках заданы два числа \(a_i\) и \(b_i\) (\(1 \leq a_i, b_i \leq N\)), задающие пару знакомых дятлов.

Выходные данные

Вывод должен содержать одно число: количество вариантов размещения по модулю K.

Примеры тестов

Примеры
Входные данные
3 2 10
1 2
1 3
Выходные данные
4
Входные данные
4 4 17
1 2
1 3
4 2
3 4
Выходные данные
0
#3383
Король
  
Быстрое преобразование Фурье

В некотором царстве жил-был король. У него была дочка – принцесса невиданной красоты. И настала пора её замуж отдать. В богатом королевстве неподалеку жил принц. И собрался король отвести принцессу, да не знает, какой маршрут выбрать. На тех землях ещё издревле было множество дорог – горизонтальных и вертикальных, и образовывали они клетчатую сетку на земле той. На перекрёстках располагались города. Город принцессы имеет координаты \((0, 0)\), а принца – \((n, m)\), уравнения дорог имеют вид \(x = x_0\) или \(y = y_0\), где \(x_0\), \(y_0\) целые. Король хочет проехать по как можно меньшему числу дорог, потому что он грабителей боится да вернуться хочет поскорей. Вам, как придворному математику, нужно посчитать, сколькими способами это можно сделать.

Входные данные

Во входном файле заданы неотрицательные целые числа \(n\) и \(m\), не превосходящие 400000.

Выходные данные

Выведите ответ на задачу в десятичной системе счисления без ведущих нулей.

Примеры
Входные данные
7 7
Выходные данные
3432
Входные данные
4 1
Выходные данные
5
#3486
5E: удалите скобки
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Дана скобочная последовательность из круглых скобок. Определить, какое минимальное количество скобок нужно удалить, чтобы получить ПСП.

Дана строка, составленная из круглых скобок. Определите, какое наименьшее количество символов необходимо удалить из этой строки, чтобы оставшиеся символы образовывали правильную скобочную последовательность.

Входные данные

Во входном файле записана строка из круглых скобок. Длина строки не превосходит \({100\,000}\) символов.

Выходные данные

Выведите единственное целое число — ответ на поставленную задачу.

Примеры
Входные данные
())(()
Выходные данные
2
Входные данные
))(((
Выходные данные
5
#3487
5C: количество ПСП
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Посчитать количество таких ПСП из двух видов скобок, что внутри пары круглых скобок нет ни одной квадратной.

Посчитайте количество правильных скобочных последовательностей длины \(2n\) (\(n\) открывающихся скобок и \(n\) закрывающихся), составленных из круглых и квадратных скобок так, что внутри любой пары круглых скобок нет квадратных скобок.

Входные данные

В единственной строке через пробел записано целое неотрицательное число \(n\), не превосходящее 1000.

Выходные данные

Выведите остаток от деления количества искомых правильных скобочных последовательностей на \(10^9+7\).

Примеры
Входные данные
1
Выходные данные
2
Входные данные
2
Выходные данные
7
#3488
5D: лексикографический порядок
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Сгенерировать все ПСП длины N.

Выведите все правильные скобочные последовательности заданной длины в лексикографическом порядке.

Входные данные

Во входном файле записана натуральное число \(n\), не превосходящее 10.

Выходные данные

Выведите все правильные скобочные последовательности длины \(2n\) в лексикографическом порядке, по одной последовательности в строке.

Примеры
Входные данные
3
Выходные данные
((()))
(()())
(())()
()(())
()()()
Страница: << 6 7 8 9 10 11 12 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест